La Bibliothèque d'Applications présente des modèles construits avec COMSOL Multiphysics pour la simulation d'une grande variété d'applications, dans les domaines de l'électromagnétisme, de la mécanique des solides, de la mécanique des fluides et de la chimie. Vous pouvez télécharger ces modèles résolus avec leur documentation détaillée, comprenant les instructions de construction pas-à-pas, et vous en servir comme point de départ de votre travail de simulation. Utilisez l'outil de recherche rapide pour trouver les modèles et applications correspondant à votre domaine d'intérêt. Notez que de nombreux exemples présentés ici sont également accessibles via la Bibliothèques d'Applications intégrée au logiciel COMSOL Multiphysics® et disponible à partir du menu Fichier.
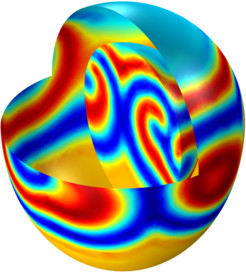
Electrical Signals in a Heart
Modeling the electrical activity in cardiac tissue is an important step in understanding the patterns of contractions and dilations in the heart. The heart produces rhythmic electrical pulses, which trigger the mechanical contractions of the muscle. A number of heart conditions involve ... En savoir plus
Diffraction Patterns
This example resembles the well-known double-slit interference experiment often demonstrated in schools with water waves or sound. The model mimics the plane-wave excitation with two thin waveguides leading to slits in a screen and computes the diffraction pattern on the opposite side of ... En savoir plus
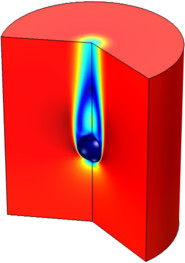
Modeling Material Removal through Thermal Ablation
This example exemplifies how to model thermal ablation by taking into account material removal. A more detailed description of the phenomenon and the modeling process can be seen in the blog post "Modeling Thermal Ablation for Material Removal". En savoir plus
Loaded Spring — Using Global Equations to Satisfy Constraints
Global equations are a way of adding an additional equation to a model. A global equation can be used to describe a load, constraint, material property, or anything else in the model that has a uniquely definable solution. In this example, a structural mechanics model of a spring is ... En savoir plus
Terminal Falling Velocity of a Sand Grain
The first stop for polluted water entering a water work is normally a large tank, where large particles are left to settle. Generally, gravity settling is an economical method of separating particles. If the fluid in the tank is moving at a controlled low velocity, the particles can be ... En savoir plus
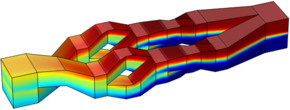
Micromixer
The development of mixers does often not only have to account for effectiveness, but also other factors must be involved, such as cost and complexity for manufacturing. The three models study a laminar static micro mixer with two parallel sets of split-reshape-recombine mixing elements. ... En savoir plus
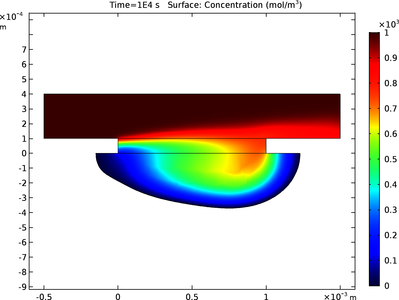
Chemical Etching
This example illustrates the principle of wet chemical etching for 2D geometry under laminar flow. The purpose of this tutorial is to examine how the copper substrate material is depleted and how the cavity shape evolves during the wet etching process. Wet chemical etching is ... En savoir plus
Automotive Muffler
This model simulates the pressure wave propagation in a muffler for a combustion engine. It uses a general approach for analysis of damping of the propagation of harmonic pressure waves. The model is solved in the frequency domain and provides efficient damping in a frequency range of ... En savoir plus
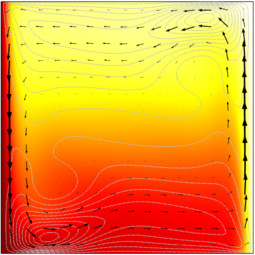
Buoyancy Flow of Free Fluids
This model couples the Navier Stokes equations and the heat transfer equations to examine density driven flow of free fluids. Here the fluid is in a square cavity with a heated wall. The buoyancy force is a Boussinesq term added to the Navier-Stokes equations. The equation is ... En savoir plus
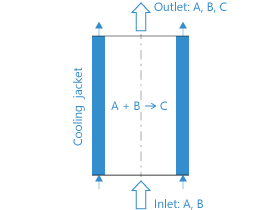
Tubular Reactor Surrogate Model Application
This tubular reactor application, together with its associated embedded model, demonstrates how the computational speed can be increased with the use of a surrogate model, as opposed to a fully-fledged finite element model. A surrogate model is a simpler, usually computationally cheaper ... En savoir plus