Optimisation topologique de structures
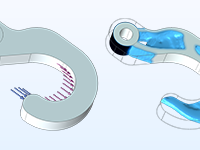
Optimisation de la topologie d'un crochet, où le matériau est distribué pour une rigidité optimale pour une masse totale donnée.
Optimisez vos modèles multiphysiques
Le module Optimization, un add-on de COMSOL Multiphysics®, fournit des outils pour l'optimisation de paramétres, de formes et de topologies, ainsi que pour l'estimation de paramètres. En l'associant à d'autres modules de la suite logicielle COMSOL, vous pouvez optimiser des dispositifs et des procédés impliquant des phénomènes tels que l'électromagnétisme, la mécanique des structures, l'acoustique, la mécanique des fluides, le transfert de chaleur, etc. Vous pouvez également optimiser les dimensions géométriques en travaillant avec le module CAD Import, le module Design ou l'un des LiveLink™ pour la CAO.
A partir d'une fonction objectif et d'un ensemble de variables de conception à optimiser, ainsi que d'un ensemble facultatif de contraintes, le logiciel recherche un design optimal. Toutes les entrées du modèle — qu'il s'agisse de dimensions géométriques, de formes de pièces, de propriétés ou de distribution des matériaux — peuvent être traitées comme des variables de design, et toute sortie du modèle peut être utilisée comme fonction objectif, à minimiser ou à maximiser.
Contacter COMSOL
Combinez le module Optimization avec l'un des add-ons COMSOL® pour appliquer l'optimisation à différents domaines physiques.

Optimisation de la topologie d'un crochet, où le matériau est distribué pour une rigidité optimale pour une masse totale donnée.
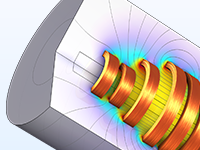
Optimisation des paramètres et de la forme d'une bobine à dix spires, par rapport à la densité de flux magnétique et la dissipation de puissance.
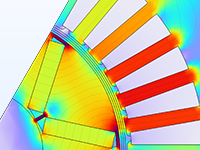
Optimisation des paramètres d'un moteur électrique pour identifier la meilleure position et la meilleure forme des aimants permanents en fonction du couple.
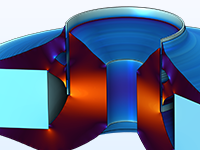
Optimisation de la topologie d'un circuit magnétique utilisé dans un haut-parleur pour réduire la réponse non-linéaire en grands déplacements.

L'optimisation de la forme du dôme et du guide d'ondes d'un tweeter de haut-parleur permet d'obtenir une courbe de réponse plus plate et un meilleur diagramme de rayonnement.
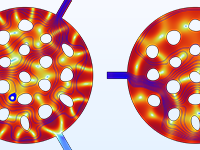
Optimisation de la forme d'un démultiplexeur acoustique; l'énergie acoustique est dirigée vers différents ports de sortie selon les bandes de fréquence.
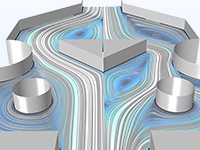
Optimisation paramétrique, de forme et de topologie d'une microvalve Tesla maximisant le rapport de chute de pression pour l'écoulement bidirectionnel.
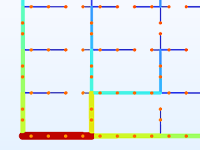
Optimisation de la topologie d'un réseau de chauffage urbain.
COMSOL Multiphysics® offre des interfaces utilisateur spécifiques avec des solveurs adaptés aux différents types d'optimisation disponibles.
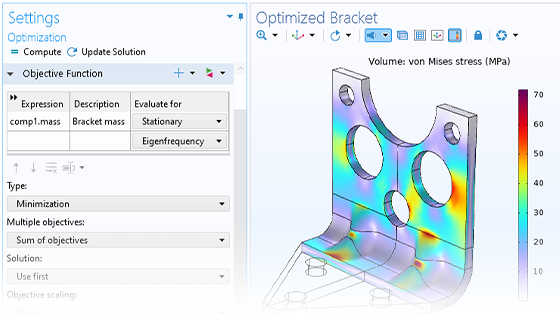
Pour mettre en place une optimisation de paramètres dans COMSOL Multiphysics®, il vous suffit d'ajouter une étude générale de type Optimisation. La fenêtre de réglages associée vous invite à ajouter une fonction objectif, des variables et des paramètres de contrôle, ainsi que des contraintes. Les paramètres que vous utilisez pour l'optimisation peuvent être les mêmes que ceux qui ont été utilisés pour configurer le modèle initialement, comme les dimensions de la géométrie, les propriétés des matériaux ou les conditions aux limites. Alors qu'une analyse paramétrique vous donnera un aperçu de l'espace des paramètres de design, une optimisation des paramètres vous fournira les paramètres optimaux et les valeurs correspondantes de la fonction objectif.
Lors de l'exécution d'une optimisation de paramètres définissant les dimensions de la géométrie, un remaillage est nécessaire à chaque itération - ce processus est entièrement automatisé avec le module Optimization. La solution optimale est toujours une véritable pièce CAO qui peut être immédiatement exportée vers des formats CAO standard. Cela nécessite le module CAD Import, le module Design ou l'un des produits LiveLink™ pour les logiciels de CAO.
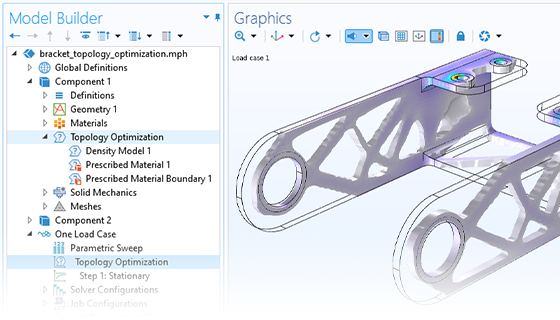
L'optimisation topologique offre une liberté de variation de la géométrie encore plus grande que l'optimisation paramétrique et l'optimisation de forme. Cette approche permet d'enlever et d'ajouter de la matière pendant le processus d'optimisation, ce qui peut amener à la création d'espaces vides qui n'étaient pas présents dans la géométrie d'origine. Cette méthode donne généralement lieu à un design organique et constitue une méthode de choix pour l'allègement des structures. Une interface utilisateur et une étude dédiées sont disponibles pour ce type d'optimisation.
L'extrême liberté de conception associée à l'optimisation topologique peut aboutir à des designs qui ne peuvent être fabriqués avec les méthodes conventionnelles. Il est donc courant d'introduire des contraintes de fabrication, car cela permet d'envisager la fabrication de la structure optimisée par extrusion ou fraisage. Tout comme pour l'optimisation de forme, le remaillage n'est pas nécessaire pour l'optimisation topologique. Le design optimal et lissé est disponible dans les formats de fichier STL, 3MF ou PLY pour une utilisation ultérieure dans un autre logiciel ou pour une analyse de vérification dans COMSOL Multiphysics®.
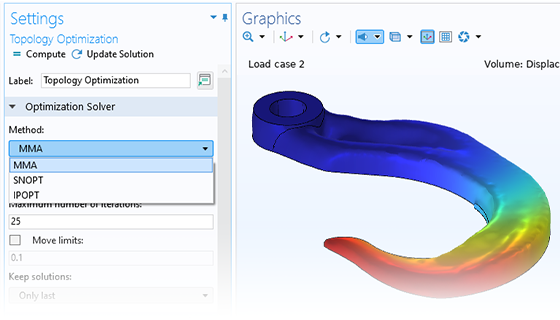
Les méthodes d'optimisation basées sur le gradient sont utilisées lorsque les dérivées peuvent être calculées efficacement à l'aide de la méthode adjointe. Celle-ci est applicable à des objectifs ou des contraintes définis par l'utilisateur, à condition que ceux-ci soient différentiables. Cela est rendu possible par la technologie de calcul différentiel symbolique, qui est intégrée au noyau de COMSOL Multiphysics® et fournit la flexibilité nécessaire à la résolution de problèmes multiphysiques personnalisés.
L'optimisation basée sur le gradient peut être employée pour des milliers, voire des millions, de variables de design. C'est souvent le cas pour l'optimisation de forme ou de topologie, où les variables représentent des quantités de champ distribuées dans l'espace et dont la valeur peut varier entre chaque élément de maillage.
Les méthodes basées sur le gradient calculent simultanément toutes les dérivées analytiques, alors que les méthodes sans dérivation doivent approximer chacune des dérivées et nécessitent donc plus de temps lorsque le nombre de variables de design augmente.
Les méthodes basées sur le gradient incluses dans le module Optimization sont les suivantes :
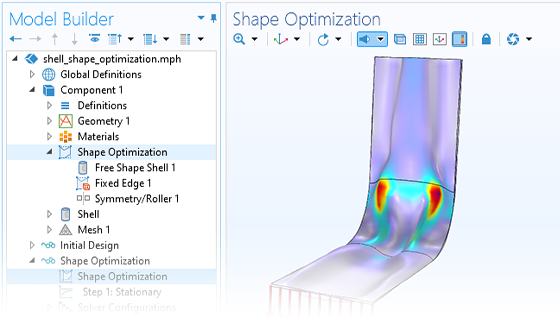
Plutôt que de faire varier un ensemble de paramètres CAO, vous pouvez autoriser à la géométrie de se déformer plus ou moins librement en utilisant des fonctionnalités prédéfinies pour l'optimisation de forme. Cette approche offre une plus grande liberté et peut parfois produire de meilleurs résultats que ceux d'une optimisation paramètrique. Un ensemble d'interfaces utilisateur dédiées est disponible pour définir simplement les déformations autorisées pour les frontières dans un modèle 2D ou 3D. En outre, une fonctionnalité dédiée à l'optimisation de forme des coques est disponible, ainsi qu'un type d'étude spécifique pour l'optimisation de forme pour le paramétrage des solveurs.
Les outils de l'optimisation de forme dans les solides sont basés sur des méthodes qui déforment le maillage d'une manière contrôlée sans qu'un remaillage soit nécessaire. La géométrie optimale est alors disponible dans un format de maillage surfacique, tel que STL, 3MF ou PLY. Cette géométrie peut ensuite être réutilisée dans une analyse séparée dans COMSOL Multiphysics® ou exportée pour être utilisée dans un autre logiciel.
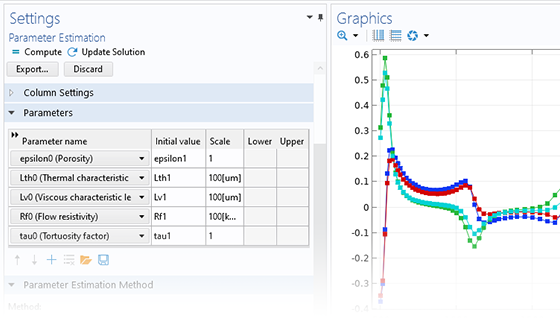
Bien que la précision d'un modèle dépende de celle des données d'entrée, il peut être difficile en pratique d'obtenir des paramètres de matériaux précis auprès des fournisseurs. Pour tenir compte des non-linéarités, vous serez peut-être amené à réaliser des expériences. Il peut toutefois s'avérer difficile de concevoir des expériences qui vous permettent d'extraire les paramètres souhaités à l'aide de méthodes analytiques.
Une solution consiste à utiliser la fonctionnalité d'estimation paramétrique du module Optimization pour trouver l'ensemble des paramètres d'un modèle qui minimise l'écart entre l'expérience et la simulation. En plus de l'interface générale pour l'estimation de paramètres, une interface utilisateur dédiée à l'ajustement des courbes à des données temporelles est rendue disponible.
La méthode d'estimation des paramètres est basée sur la méthode des moindres carrés et peut être utilisée lorsque les données de référence sont une fonction du temps ou d'un seul paramètre. Dans la plupart des cas, vous obtiendrez une estimation de la variance et de la fiabilité des paramètres estimés.
Pour s'initier à l'estimation de paramètres, une application prête à l'emploi est disponible. Elle permet d'utiliser des données provenant de tutoriels ou de fichiers de mesures importées, ainsi que de saisir des expressions personnalisées pour spécifier la courbe à ajuster.
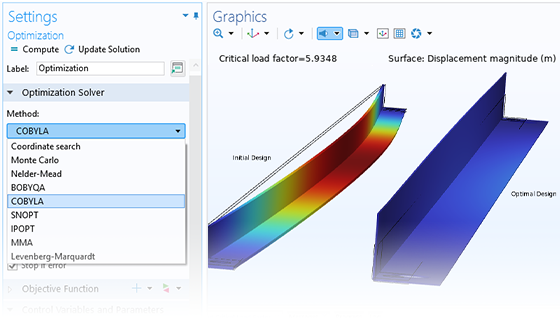
Les méthodes d'optimisation sans gradient sont utilisées lorsque les directions de recherche nécessaires au solveur d'optimisation ne peuvent être calculées qu'indirectement. C'est souvent le cas pour l'optimisation des paramètres où les variables de contrôle représentent les dimensions de la géométrie et où le remaillage est nécessaire à chaque itération.
Les méthodes sans gradient incluses dans le module Optimization sont les suivantes :
L'utilisation du Constructeur d'applications avec le module Optimization offre la possibilité à un plus grand nombre d'utilisateurs de réaliser des études d'optimisation de manière indépendante, sans avoir besoin de consulter un expert en simulation.
Les modèles d'optimisation peuvent par exemple inclure une estimation des paramètres basée sur des données expérimentales. Une application adaptée à cette tâche particulière permettrait à l'utilisateur de saisir un ensemble de données expérimentales sans se soucier des détails du modèle d'optimisation mis en oeuvre.
L'utilisation d'applications permet par ailleurs une résolution plus efficace des problèmes de commande optimale. Le module Optimization peut être utilisé pour identifier quelle entrée transitoire donne une réponse transitoire donnée. Dans ce cas, vous souhaitez ajuster la réponse souhaitée à partir de résultats expérimentaux. La création d'une application pour cette tâche permet de regrouper la complexité de ce processus dans une interface utilisateur personnalisée, permettant à divers utilisateurs d'exécuter des simulations de commande optimale en spécifiant simplement les sorties souhaitées.
Chaque activité et chaque besoin en matière de simulation sont différents. Afin d'évaluer pleinement si le logiciel COMSOL Multiphysics® répond ou non à vos exigences, nous vous invitons à nous contacter. En parlant à l'un de nos représentants, vous obtiendrez des recommandations personnalisées et des exemples détaillés qui vous aideront à tirer le meilleur parti de votre évaluation et vous guideront pour choisir les options de licence les mieux adaptées à vos besoins.
Il vous suffit de cliquer sur le bouton "Contacter COMSOL", d'indiquer vos coordonnées et tout commentaire ou question spécifique, avant de soumettre votre demande. Vous recevrez une réponse d'un représentant de COMSOL très rapidement.
Demander une démonstration du logiciel