
Heat Transfer with Radiation in Participating Media and the Discrete Ordinates Method
A medium subjected to internal heat radiation is considered participating if it absorbs, emits, or scatters thermal rays as they travel through the medium. In this blog post, we give an introduction to scattering modeling with an in-depth discussion of the discretization method, which uses a discrete set of directions for heat radiation.
About Scattering in Participating Media
Earth’s atmosphere is an example of a participating medium, as its particles interact with solar irradiation. Absorption and emission of energy are due to energy transfer at the molecular or atomic scales, whereas scattering consists of diffraction, reflection, and refraction of incident energy onto molecules of the participating medium (Ref. 1), resulting in a spatial redistribution of the incident energy. Examples of effects of a participating medium on incident radiation are represented in the figure below.
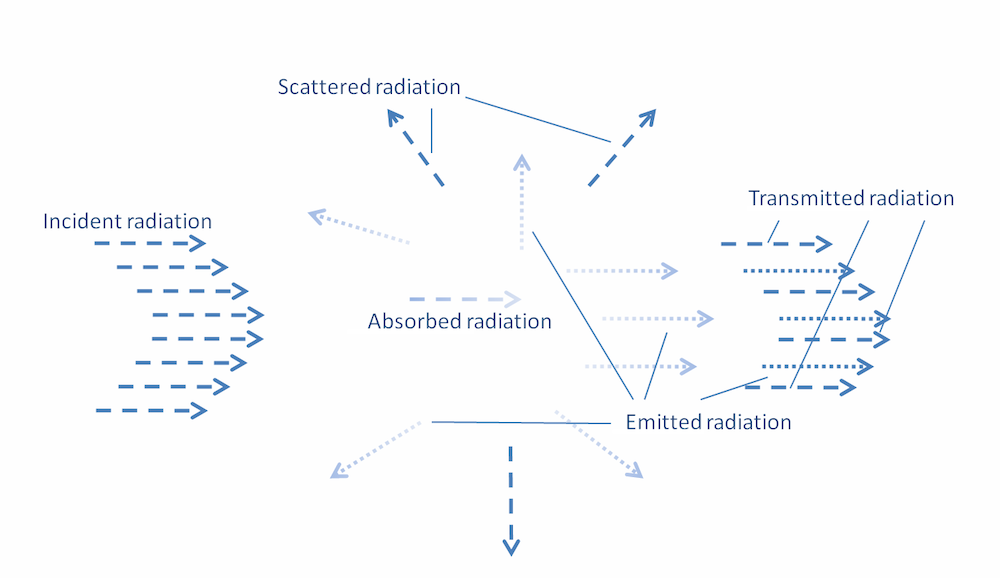
Examples of interactions between participating media and radiation.
In the Heat Transfer Module, an add-on to the COMSOL Multiphysics® software, the radiative transfer equation is discretized by means of the discrete ordinates method. This method is based on a number of discrete directions for the radiation and associated quadrature weights used for numerical integration. The combination of a set of discrete directions and associated quadrature weights is called a quadrature set. We will explain and compare the quadrature sets of the physics interfaces that are used for radiation in absorbing media and heat transfer with radiation in participating media.
Let’s consider a participating medium. The conservation equation for the radiative intensity, I, transported in the direction (or, in this case, unit vector) {\bf s}, known as the radiative transfer equation (RTE), is
(1)
{\bf s} \cdot \nabla I({\bf r},{\bf s}) & = \kappa I_{\rm b}(T) – (\kappa + \sigma_{\rm s})I({\bf r},{\bf s}) + \mathcal{S}({\bf r},{\bf s}),\\
\mathcal{S}({\bf r},{\bf s}) & = \frac{\sigma_s}{4\pi} \int \limits_0^{4\pi}\phi({\bf s},{\bf s}’)I({\bf r},{\bf s}’)d\Omega’,
\end{split}
where \kappa is the absorption coefficient, \sigma_{\rm s} is the scattering coefficient, and I_{\rm b} is the blackbody radiative intensity.
Further, d \Omega=\sin\psi d \psi d \varphi is the infinitesimal solid angle, in steradians (sr), in which \psi and \varphi are the polar angle and the azimuthal angle in spherical coordinates (r,\psi,\varphi) of the direction (of unit vector) {\bf s}, as shown in the figure below. In Eq. 1, the quantity \kappa I ({\bf r},{\bf s}) of energy is absorbed; \kappa I_{\rm b} (T)is emitted; and \mathcal{S} ({\bf r},{\bf s}) is the quantity of energy that is scattered from any direction of propagation to {\bf s}. Finally, \sigma_{\rm s} I ({\bf r},{\bf s}) is the quantity of energy that is scattered from {\bf s} to any direction of propagation.
The challenge here is in the discretization of the integral term \mathcal{S}, which necessitates a set of n pairs of discrete direction, {\bf s}_i, and quadrature weight, {\bf \omega}_i; namely a quadrature set \big((\omega_i,{\bf s}_i)\big)_{1 \leq i \leq n}. That quadrature set allows for the numerical discretization of the unit sphere:
In order to know the incident energy or incident radiation, G, at any point in a participating medium wherein energy is transported in discrete directions ({\bf s}_i)_{1\leq i \leq n}, Eq. (1) is solved for each radiative intensity, I_i, 1\leq i \leq n, transported in the discrete direction {\bf s}_i. Numerical approximations to the incident radiation, G({\bf r})=\int I({\bf r},{\bf s}) d\Omega, the radiative heat flux, {\bf q}_{\rm r}({\bf r})=\int I({\bf r},{\bf s}) {\bf s} d\Omega, and the scattering term, \mathcal{S}, are
(2)
G({\bf r}) & \approx \sum_{i=1}^{n} I_i({\bf r}) \omega_i, \\
{\bf q}_{\rm r}({\bf r}) & \approx \sum_{i=1}^{n} I_i({\bf r}) {\bf s}_i \omega_i, \\
\mathcal{S}({\bf r},{\bf s}_i) & \approx \frac{\sigma_s}{4\pi} \sum \limits_{j=0}^n \phi({\bf s}_i,{\bf s}_j) I_j({\bf r}) \omega_j.
\end{split}
Integrating Eq. 1 over all directions yields the conservation of incident radiation
(3)
\nabla \cdot {\bf q}_{\rm r} & = – Q_{\rm r}, \\
Q_{\rm r} & = \kappa(G-4\pi I_{\rm b}).
\end{split}
As for the conservation of energy, the radiative heat flux, {\bf q}_{\rm r}, is added to the thermal flux, {\bf q} = – k \nabla T, so that the stationary energy equation that accounts for radiation reads
or
(4)
Accurate computation of Eq. 2, hence accurate conservation of incident radiation Eq. 3 and accurate conservation of energy in heat transfer with radiation in participating media Eq. 4, depends on the quadrature set \big((\omega_i,{\bf s}_i)\big)_{1 \leq i \leq n}. The design of quadrature sets is discussed below.
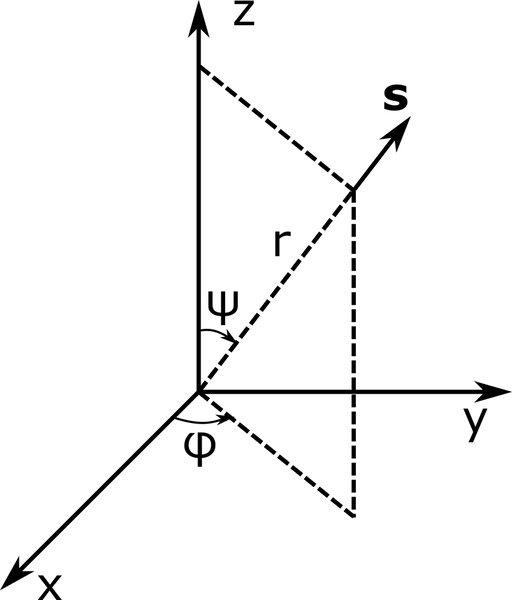
Spherical coordinates for the absorbing, emitting, and scattering medium.
Generating Quadrature Sets
Consider a medium that absorbs, emits, and scatters energy. For an accurate computation of the scattering term, several moments need to be satisfied (Ref. 1). For instance, the zeroth, first, and second moments are
\int \limits_0^{4\pi} d\Omega & = 4\pi \approx \sum\limits_{i=1}^n \omega_i, \\
\int \limits_0^{4\pi} {\bf s} d\Omega & = 0 \approx \sum\limits_{i=1}^n \omega_i {\bf s}_i, \\
\int \limits_0^{4\pi} {\bf s}{\bf s}^\intercal d\Omega & = \frac{4\pi}{3}I_3 \approx \sum\limits_{i=1}^n \omega_i {\bf s}_i{\bf s}_i^\intercal.
\end{split}
All quadrature sets of the physics for the Radiation in Participating Media and Radiation in Absorbing-Scattering Media interfaces satisfy these conditions with good accuracy. The conditions above allow for accurate approximation of \int {\bf s}^k I({\bf r},{\bf s}) d\Omega, k\in \{0,1,2\} and are thus expected to yield accurate results for heat transfer with radiation in absorbing, emitting, and second-order polynomial anisotropic scattering media (that is, for a phase function of the form \phi({\bf s}_i,{\bf s }_j)= \sum \limits_{k=0}^2\alpha_k ({\bf s}_i\cdot{\bf s}_j)^k). For p^{\rm th}-order anisotropic scattering, the challenge is in designing a quadrature set that yields accurate approximation to \int {\bf s}^k I({\bf r},{\bf s}) d\Omega, k\in \{0,\ldots,p\}.
Several quadrature sets are available in the Radiation in Participating Media and Radiation in Absorbing-Scattering Media interfaces, namely:
- Level symmetric even (LSE)
- Level symmetric hybrid (LSH)
- Equal weight odd (EWO)
- Quasiuniform
LSE, LSH, and EWO are conditioned quadrature sets that differ in their higher-order moment conditions. (You can refer to Ref. 2 for further information.) A discretization of order N is denoted SN and has N(N+2) discrete directions in 3D. For the same order of discretization, say S6, the quadrature sets LSH and EWO are expected to yield better approximation to the heat flux according to Ref. 2. This assertion will be discussed further in a following section. However, it is known that the computation of the radiative heat flux at walls is more accurate when the first moment is satisfied hemispherically (Ref. 1), meaning
(5)
hence the need to discuss and compare the performance of quadrature sets in arbitrary geometries, wherein Eq. 5 is a priori not satisfied for all boundaries.
Quasiuniform quadrature sets are generated geometrically. A discretization of order N is denoted TN and has 8N^2 discrete directions in 3D, meaning N^2 directions in the first octant \{(x,y,z),x \geq 0,y \geq 0, z \geq 0 \}. To provide the discretization T2 (alternatively, T3), the set \{(x,y,z)\in[0,1]^3,x+y+z=1\} is discretized into 2^2 (or 3^2, respectively) equilateral triangles. These triangles are then projected onto the unit sphere, yielding a discretization of the first octant, \{(x,y,z)\in[0,1]^3,x^2+y^2+z^2=1\}. Discretizations of the other seven octants are obtained by symmetries. Higher-order discretizations T2 \cdot 2^p (or T3 \cdot 2^p) are here obtained by successive refinements of the reference set T2 (or T3). (You can read more about quasiuniform quadrature sets in Ref. 3–4)
Conditioned quadrature sets LSE, LSH, and EWO are expected to perform better than geometrical quadrature sets for a given number of discrete directions and for simple geometries (planar boundaries aligned with axis), wherein Eq. 5 is satisfied. In complex geometries with arbitrarily oriented boundaries, Eq. 5 is a priori not satisfied at each boundary. In this case, the accuracy advantage of these quadrature sets may be lost and result in an accuracy for the radiative heat flux and energy balance that is comparable to those of the geometrically generated quadrature set with the same number of discrete directions.
The main interest in geometrical quadrature sets is that they can be designed with a very high number of discrete directions. (The Heat Transfer Module supports up to 512 directions using T8 in 3D, but it would be straightforward to generate higher-order discretizations, like T16. However, it would then be very demanding from a computational point of view.) On the other hand, conditioned quadrature sets are limited in their number of discrete directions (168 directions are used in S12; higher-order discretizations, like S14, are useless because they have negative weights and yield unphysical results).
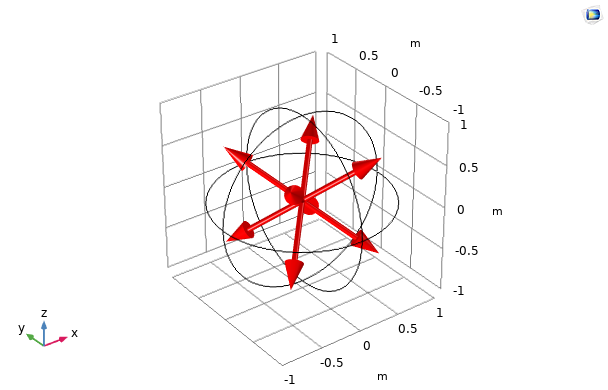
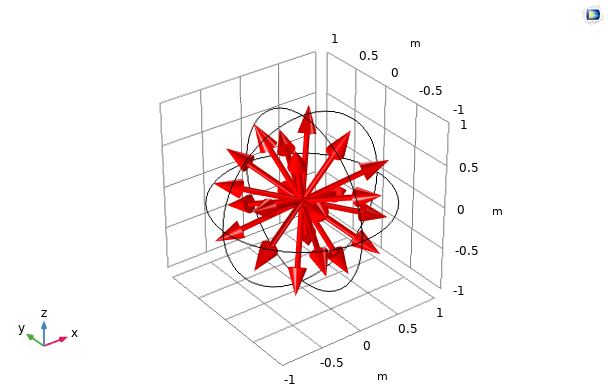
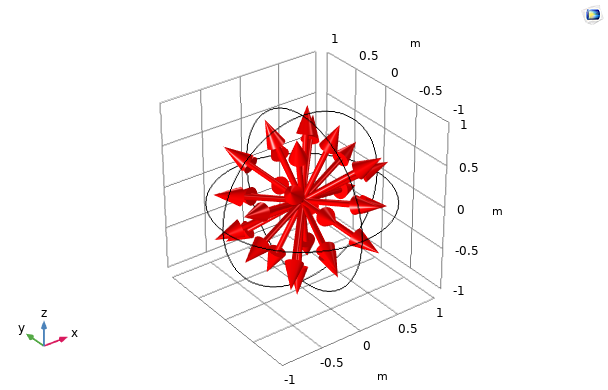
Discrete directions ({\bf s}_i)_{1 \leq i \leq n} of quadrature sets S2, LSE S4, and T2 are presented below.
Discrete directions of quadrature sets S2 (left), LSE S4 (middle), and T2 (right) with 8, 24, and 32 directions in three dimensions, respectively.
Effects of the number of discrete directions are studied in the next section. The quadrature sets S2, LSE S6, LSH S6, EWO S6, T3, and T8 are compared in two examples, which have 2D setups. The number of discrete directions in 2D are:
| Quadrature Set | Discrete Directions |
|---|---|
| S2 | 4 |
| LSE S6 | 24 |
| LSH S6 | 24 |
| EWO S6 | 24 |
| T3 | 36 |
| T8 | 256 |
Example 1: Radiation in Absorbing Media
Here, we consider a model of a participating medium that only absorbs energy — it does not scatter or emit energy. The RTE reduces to
subject to appropriate boundary conditions.
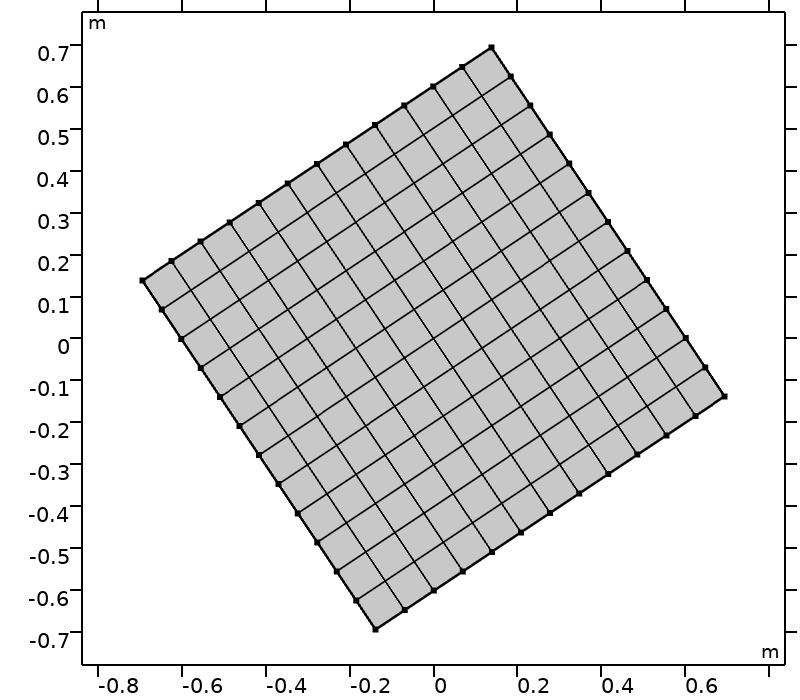
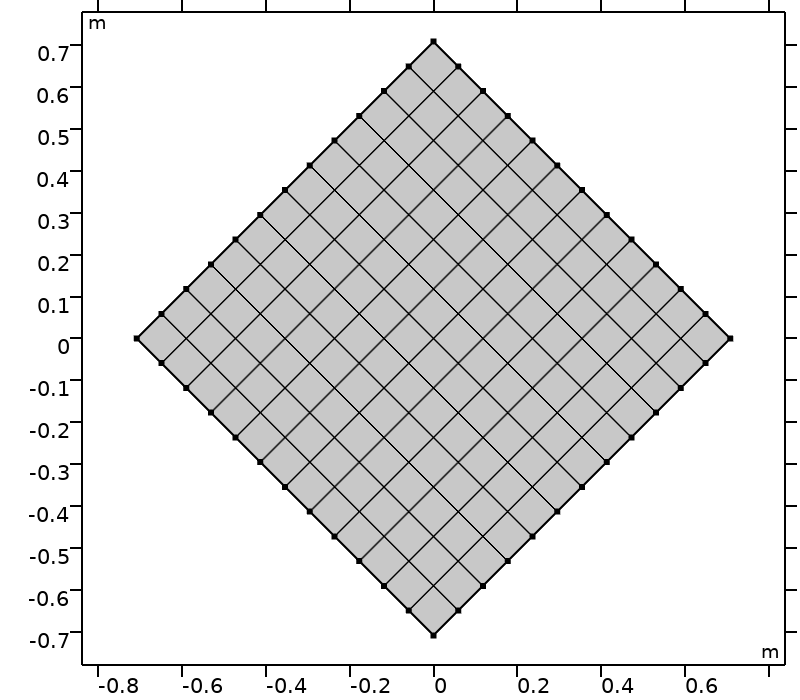
To assess the performance of quadrature sets in complex geometries, the computational domain is rotated. The computational domain \mathcal{D} (\theta) is the domain obtained by applying the rotation of center (0,0) and angle \theta to the reference domain, \mathcal{D}(0) = [-0.5,0.5]^2, as seen in the figures below.
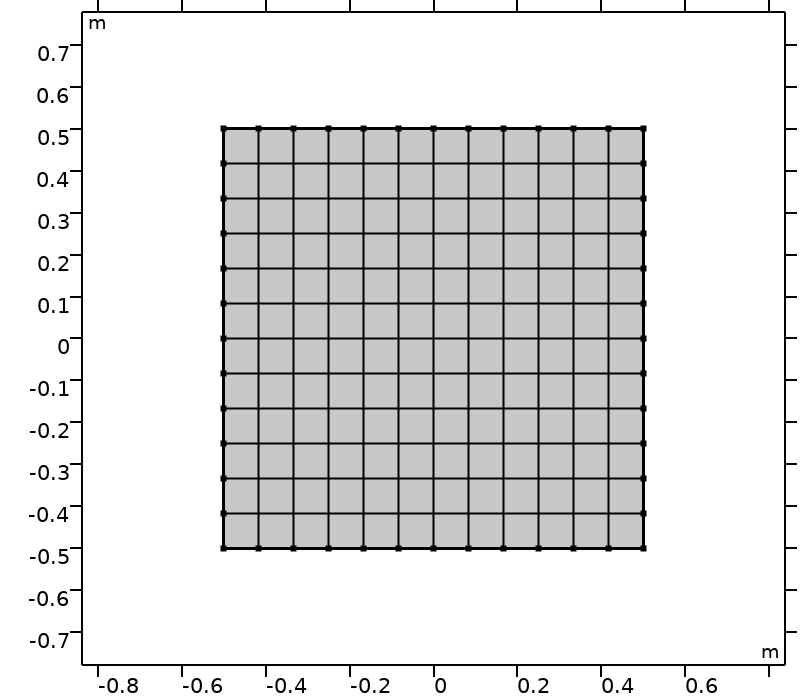
|
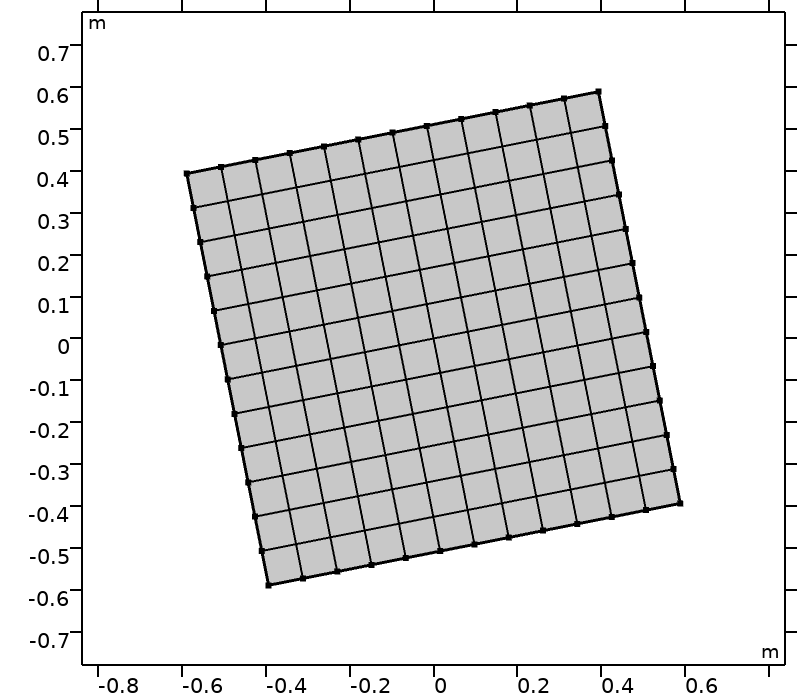
|

|
|
|
Computational domains \mathcal{D}(\theta) and \theta \in \big \{ k \pi /16, k \in \{0,\ldots,4\}\big \}.
As a boundary condition, consider an incident intensity, I_{\rm w} (meaning I_i=I_{\rm w}, \; {\bf n} \cdot {\bf s}_i < 0, \; i \in \{1,\ldots,n\}), on \partial \mathcal{D}(\theta). The analytical solution to this problem is given in the appendix: The energy is absorbed exponentially. The error in the incident irradiation obtained numerically, G_{\rm num}, compared to the analytical solution obtained with the discretization T8, G_{\rm T8}, is quantified as
The error in the energy balance is quantified as
with Q_{\rm r} and {\bf q}_{\rm r} being the radiative heat source and the radiative heat flux, respectively.
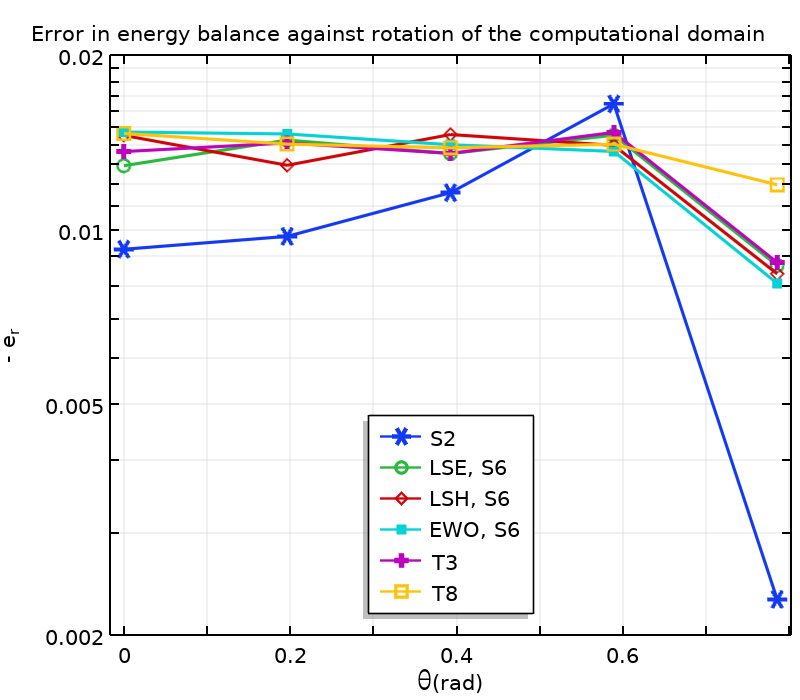
Results obtained on a 144-element mapped domain are given in the plot below.
Errors in average incident irradiation (left) and the energy balance (right) for different discretizations and rotations of the computational domain. The errors are given for rotations \theta_k = k \pi /16, k \in \{0,\ldots,4\}.
As expected, the higher the number of discrete directions, the better the numerical solution of incident radiation. For a discretization of S6, LSH outperforms LSE and EWO. Note that the results obtained with T3 are very close to those obtained with LSH S6, but the number of discrete directions with T3 is higher than with LSH S6. This suggests that conditioned quadrature sets outperform geometrical quadrature sets for a given number of discrete directions.
All methods yield a satisfactory energy balance. Note that for this particular test case, the energy balance may be flawed for a higher number of discrete directions. Indeed, some discrete directions are nearly collinear to boundaries, and the mesh used there may not be fine enough to resolve strong gradients of these radiative intensities and thus the radiative heat flux. Of course, the error in the energy balance may be lowered by refining the mesh. This effect is reduced in general situations wherein some energy is also emitted and scattered in all directions. Next up, we look at the effects of quadrature sets when coupled with the heat equation.
Example 2: Heat Transfer with Radiation in Participating Media
In this section, quadrature sets are compared for modeling heat transfer with radiation in absorbing, emitting, and scattering media. The equations to be solved are
\nabla \cdot (-k\nabla T) & = \kappa\left(G-4\pi I_{\rm b}(T)\right), \\
{\bf s}_i \cdot \nabla I_i & = \kappa I_{\rm b}(T)-(\kappa+\sigma_{\rm s}) I_i + \frac{\sigma_{\rm s}}{4\pi}\sum\limits_{j=1}^n \phi({\bf s}_i,{\bf s_j})\omega_j I_j,\; i \in \{1,\ldots,n\},
\end{split}
subject to appropriate boundary conditions.
The computational domain is the same as that used in the first example. The scattering albedo, \sigma_{\rm s}/(\kappa+\sigma_{\rm s}), is set to 1/2. The phase function is chosen to be polynomial anisotropic of the second order; that is, of the form \phi({\bf s}_i,{\bf s}_j) = 1+ a_1 P_1 ({\bf s}_i\cdot{\bf s}_j)+ a_2 P_2 ({\bf s}_i\cdot{\bf s}_j) with (a_1,a_2)=(0.5,0.1), where P_p is the Legendre polynomial of order p. The phase function is normalized so that \int \limits_0^{4\pi} \phi d\Omega = 4\pi. Boundaries are opaque surfaces with a surface emissivity of 0.5. Boundary conditions are then applied for the temperature:
- T_{\rm bottom}\left(X(\theta)\right)=T_0+(T_1-T_0)\exp\left(-\big(X(\theta)/(0.2[{\rm m}])\big)^2\right) with X(\theta)=(x+y\tan\theta)/\sqrt{1+\tan^2\theta} at the bottom boundary
- {\bf q}\cdot {\bf n}=h(T-T_0) at the top boundary
- Thermal insulation at the left and right boundaries
As for the parameters, they are (T_0,T_1,h)=(300 \textrm{ K},400 \textrm{ K},10 \textrm{ W.m}^{-2}.{\rm K}^{-1}).
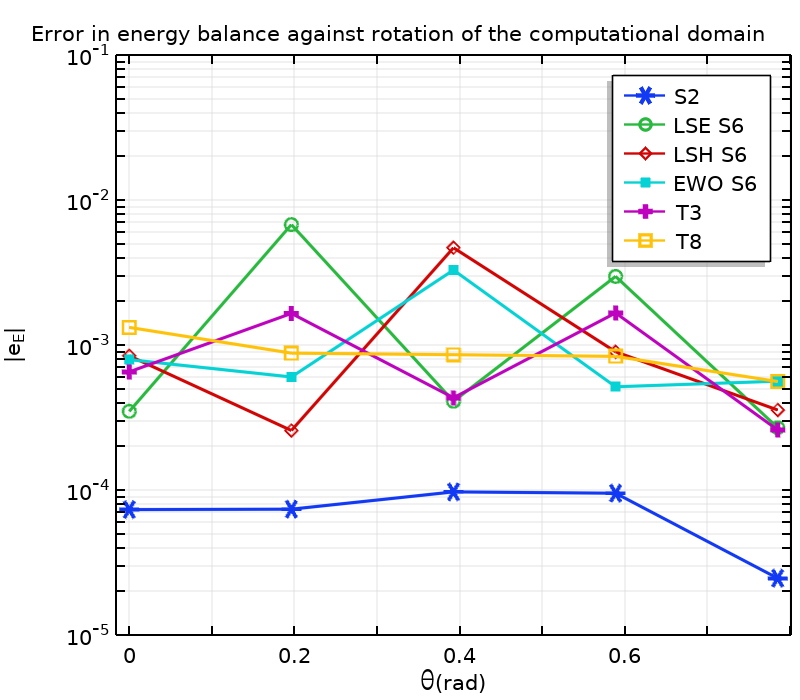
Quadrature sets are compared quantitatively by making use of the relative error in the energy balance
with Q_{\rm r} being the radiative heat source and {\bf q} the thermal flux.
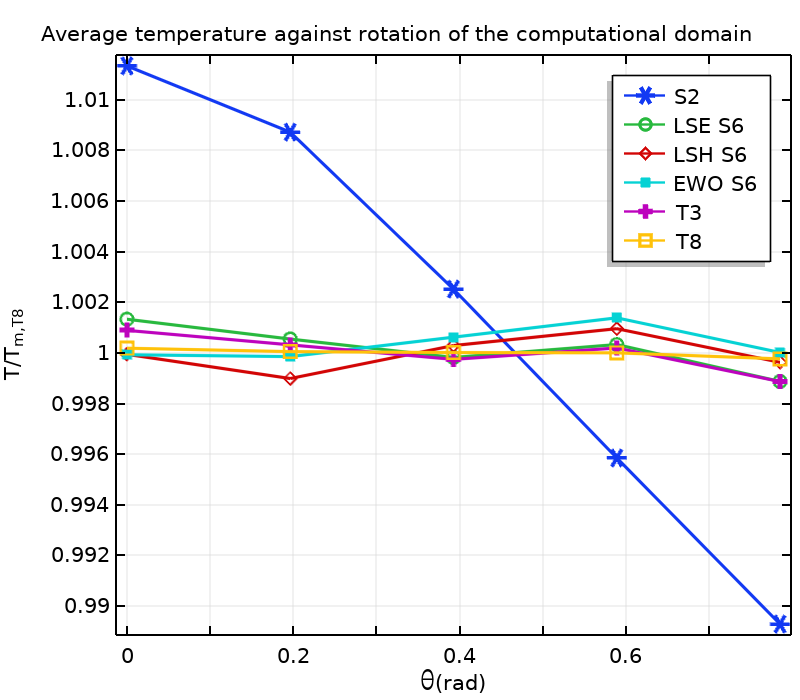
Also, the effect of rotating the domain on the temperature and incident radiation fields is tested. Results of the average temperature, average incident radiation, and energy balance error are shown below. Standard deviations of average temperature and average radiation are given in the following table.
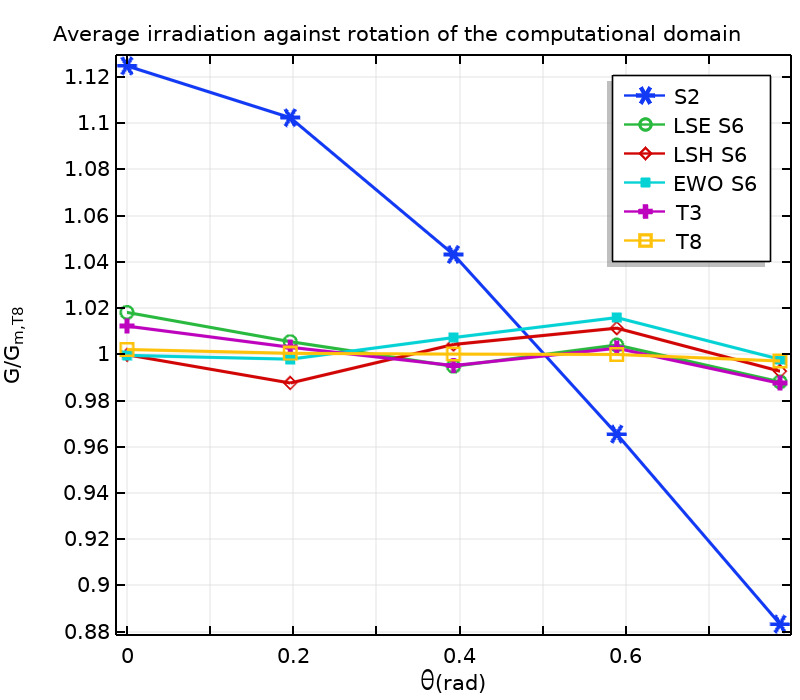
Energy balance (left), average incident temperature (middle), and average incident radiation (right) for different discretizations and rotations of the computational domain. Values are given for rotations \theta_k = k \pi /16, k \in \{0,\ldots,4\}. Temperatures and incident radiations are made dimensionless with the mean average temperature, T_\textrm{m,T8}=324.03 \ {\rm K}, and incident radiation, G_\textrm{m,T8}=2510.0 \ {\rm W.m^{-2}}, obtained with T8.
| Standard Deviations | Average Temperature | Average Incident Radiation |
|---|---|---|
| S2 | 2.33 | 197.7 |
| LSE S6 | 0.22 | 21.6 |
| LSH S6 | 0.23 | 22.7 |
| EWO S6 | 0.20 | 18.4 |
| T3 | 0.18 | 17.4 |
| T8 | 0.04 | 3.2 |
Standard deviations of average temperature, \sigma(T_{\rm av}) \ {\rm [K]}, and average incident radiation, \sigma(G_{\rm av}) \ [{\rm W.m^{-2}}].
All methods yield a satisfactory energy balance. The angular resolution is definitely not fine enough with S2, resulting in large variations in the incident radiation and temperature fields with respect to rotating the computational domain. These variations exhibit a similar pattern, as the heat equation and the RTE are strongly coupled. The dependency of the results on the rotation of the domain is reduced with an increasing number of discrete directions. Given the standard deviations in the table, results obtained with EWO show less dependency on the rotation of the domain compared with LSE and LSH. Standard deviations are even lower with further discrete directions for T3 and T8. Note that the energy balance strongly depends on the rotation of the domain, except for T8 here. This may be due to the fact that Eq. 5 is not satisfied for \theta \neq 0, resulting in inaccurate computation of radiative heat fluxes at boundaries when the number of discrete directions is rather small (compared with T8 here).
Concluding Thoughts on the Discrete Ordinates Method
In this blog post, quadrature sets used for the discrete ordinates method in the COMSOL Multiphysics® software have been presented and discussed. Conditioned quadrature sets like LSE, LSH, and EWO are expected to perform better than geometrical quadrature sets for a given number of discrete directions. Conditioned quadrature sets have a limited number of discrete directions. Thus, geometrical quadrature sets are of interest to reach higher angular resolution.
To further imagine simulations with complex geometries, we have also studied the effects of rotating a square computational domain on incident radiation, temperature, and energy balance. For the test case of radiation in an absorbing medium, the results obtained with LSE exhibit more dependency on rotating the computational domain compared with LSH and EWO, but LSH outperforms the other conditioned quadrature sets, EWO and LSE, given its better agreement with analytical results. For the example of heat transfer with radiation in participating media, the higher the number of discrete directions, the less dependent the results are on the rotation of the computational domain. However, for a rather small number of discrete directions (all quadrature sets tested in this blog post, except T8), results showed dependence on rotating the computational domain — it is thus relevant to test the effect of the number of discrete directions in a convergence study.
Try modeling the heat transfer examples shown here:
- Discrete Ordinates Quadrature Sets for Radiation in Absorbing Medium
- Discrete Ordinates Quadrature Sets for Heat Transfer with Radiation in Participating Medium
References
- M.F. Modest, Radiative Heat Transfer, Academic Press, 2003.
- W.A. Fiveland, “The Selection of Discrete Ordinate Quadrature Sets for Anisotropic Scattering,” Fundamentals of Radiation Heat Transfer, vol. 160, pp. 89–96, 1991.
- C.P. Thurgood, A. Pollard, and H.A. Becker, “The TN Quadrature Set for the Discrete Ordinates Method,” Journal of heat transfer, vol. 117, no. 4, pp. 1068–1070, 1995.
- M.A. Badri, P. Jolivet, B. Rousseau, S. Le Corre, H. Digonnet, and Y. Favennec, “Vectorial Finite Elements for Solving the Radiative Transfer Equation,” Journal of Quantitative Spectroscopy and Radiative Transfer, vol. 212, pp. 59–74, 2018.
Appendix
The analytical solution to the problem
\begin{cases}
{\bf s}_i \cdot \nabla I_i + \kappa I_i = 0 \textrm{ on }\mathcal{D}(\theta), \\
{\bf n} \cdot {\bf s}_i \textless 0 \Rightarrow I_i = I_{\rm w} \textrm{ on }\partial\mathcal{D}(\theta)
\end{cases}
is
\forall i \in \{1,\ldots,n\},\forall (x,y)\in \mathcal{D}(\theta), I_i(x,y) & =
\begin{cases}
I_{w}\exp\left(-\alpha \textrm{ if}\left(Y+\tfrac{1}{2}\textgreater r (X+\tfrac{1}{2}),(X+\tfrac{1}{2})S_{X,i}(1+r^2),
(Y+\tfrac{1}{2})S_{Y,i}(1+\tfrac{1}{r^2})\right)\right), & S_{X,i}\geq 0,\;S_{Y,i}\geq 0, \\
I_{w}\exp\left(-\alpha\textrm{ if}\left(Y-\tfrac{1}{2}\textless r(X-\tfrac{1}{2}),(X-\tfrac{1}{2})S_{X,i}(1+r^2),
(Y-\tfrac{1}{2})S_{Y,i}(1+\tfrac{1}{r^2})\right)\right), & S_{X,i}\textless0,\;S_{Y,i}\textless0, \\
I_{w}\exp\left(-\alpha\textrm{ if}\left(Y-\tfrac{1}{2}\textgreater r(X+\tfrac{1}{2}),(Y-\tfrac{1}{2})S_{Y,i}(1+r^2),
(X+\tfrac{1}{2})S_{X,i}(1+\tfrac{1}{r^2})\right)\right), & S_{X,i}\geq 0,\; S_{Y,i}\textless0, \\
I_{w}\exp\left(-\alpha\textrm{ if}\left(Y+\tfrac{1}{2}\textless r(X-\tfrac{1}{2}),(Y+\tfrac{1}{2})S_{Y,i}(1+r^2),
(X-\tfrac{1}{2})S_{X,i}(1+\tfrac{1}{r^2})\right)\right), & S_{X,i}\textless0,\; S_{Y,i}\geq 0,
\end{cases} \\
\alpha & = \frac{\kappa}{S_{X,i}^2+S_{Y,i}^2}, \\
S_{X,i}(\theta) & = s_{x,i}\cos\theta+s_{y,i}\sin\theta, \\
S_{Y,i}(\theta) & = s_{y,i}\cos\theta-s_{x,i}\sin\theta, \\
r & = \frac{S_{Y,i}}{S_{X,i}},\\
X(\theta) & = \frac{x+y\tan\theta}{\sqrt{1+\tan^2\theta}}, \\
Y(\theta) & = \frac{-x\tan\theta+y}{\sqrt{1+\tan^2\theta}}.
\end{split}
Notations
(a_i)_{1\leq i \leq n} Legendre coefficients [1]
G incident radiation [W.m-2]
h heat transfer coefficient [W.m-2.K-1]
(I_i)_{1\leq i \leq n} radiative intensities [W.m-2.sr-1]
I_{\rm b} blackbody radiative intensity [W.m-2.sr-1]
I_{\rm w} incident radiative intensity [W.m-2.sr-1]
kthermal conductivity [W.m-1.K-1]
\kappa absorption coefficient [m-1]
{\bf n} outward-pointing normal vector [1]
(\omega_i)_{1\leq i \leq n} quadrature weights [sr]
\Omega solid angle [sr]
(\Delta\Omega_i)_{1\leq i \leq n} discrete solid angles [sr]
\phiscattering phase function [1]
\varphi azimuthal angle [rad]
\psi polar angle [rad]
{\bf q} thermal flux [W.m-2]
{\bf q}_{\rm r} radiative heat flux [W.m-2]
Q_{\rm r} radiative heat source [W.m-3]
{\bf r} position vector [m]
{\bf s} direction of transport [1]
({\bf s}_i)_{1\leq i \leq n} discrete directions [1]
\mathcal{S}({\bf r},{\bf s}) scattering term [W.m-3]
\sigma(V) standard deviation of variable V[V]
\sigma_s scattering coefficient [m-1]
T temperature [K]
\theta rotation angle of computational domain [rad]





Comments (1)
Domenico Lahaye
January 8, 2021Many thanks for this wonderful explanation!
When using the discrete ordinate method in Comsol, we observe a increase in the total number of degrees of freedom that does not match with our intuition.
Could you please comment of how you understand the increase in number of degrees of freedom with using the discrete ordinate method?
Thank you in advance.
Domenico Lahaye.