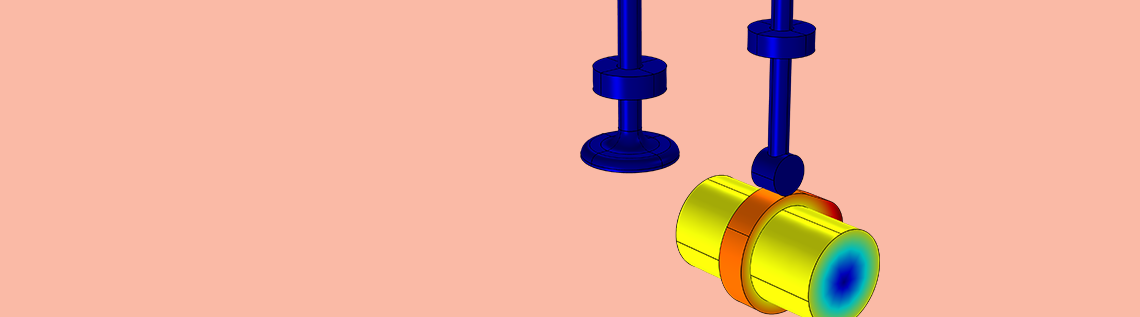
When working with multibody systems, you may need to model a mechanism that transfers motion from one component to another. The mechanism used to implement this behavior, known as a cam-follower mechanism, plays an important role in many applications, including internal combustion engines, printing control mechanisms, textile weaving machines, and valves. You can easily model this type of mechanism with the Cam-Follower feature in the COMSOL® software. Let’s take a look at this feature in detail.
Classifying the Different Types of Cam-Follower Mechanisms
Cam-follower mechanisms are categorized based on the input and output motion of their configurations. The different types of cam-follower mechanisms are described below.
Rotating Cam, Translating Follower
When a follower moves along a guide while a cam rotates, the motion is categorized as a rotating cam and translating follower. This is further categorized based on the motion of the follower. If the motion is along the axis passing through the center of rotation of the cam, then it is called a radial inline follower, whereas if the motion is along an offset from the axis, it is called a radial offset follower.
Animation showing the displacement and velocity plot of the radial inline follower.
Animation showing the displacement and velocity plot of the radial offset follower.
Rotating Cam, Oscillating Follower
When the rotary motion of the cam is converted into oscillatory motion, the configuration is known as a rotating cam and oscillatory follower.
Animation showing an example of an oscillatory cam and follower.
Translating Cam, Translating Follower
In this case, both the cam and follower exhibit translational motion. This means that the motion to the follower is due to the profile height of the cam.
Animation showing a displacement plot of a wedge cam.
Stationary Cam, Moving Follower
There are cases in which the cam is stationary and the follower traces the profile of the cam. This type of arrangement is classified as a stationary cam and moving follower.
Animation showing displacement plot of a stationary cam and moving follower.
Point Follower
A point follower is a mechanism in which a pin on a follower slides in a slot. The slot can be of any profile.
Animation showing a displacement plot of a pin moving in a curved slot.
Combined Motion
There are many ways to transform one type of motion into another. The variety of the cam-follower mechanism is limited only by your own imagination. For example, you can use a combination of the above configurations to generate a combined effect. A few common examples are barrel cams and end cams, which are used to convert rotary motion into translational and oscillatory motion.
Animation showing the combined translational and oscillatory motion of a barrel cam.
Using the Cam-Follower Joint Type
The Cam-Follower joint type, available with the Multibody Dynamics Module as of COMSOL Multiphysics® software version 5.3a, is used to model applications in which a point follows a surface. In other words, the contact is unique and occurs at a single point.
Usually, the active component is called the cam and the passive component is called the follower, but in the COMSOL® software, this feature is built in such a way that you can model both components as either active or passive.
With the default settings, the cam and follower will always remain in contact, which means that no chattering is allowed. To model intermittent contact, the Activation Conditions feature under the Cam-Follower joint type can be used. In addition, the cam and follower can both be modeled as rigid or flexible components.
In order to ensure that the point on the follower always follows the specified cam surface, an offset from the cam boundary is defined such that the gap distance is always zero. The implementation of these constraints follows this procedure:
- Based on the selected cam surface, a search algorithm is used to find the closest point on the cam surface with respect to the specified follower point
- The internal gap variable is defined such that the difference of absolute vectors between a point on the follower and the closest point on the cam is set to a predefined offset
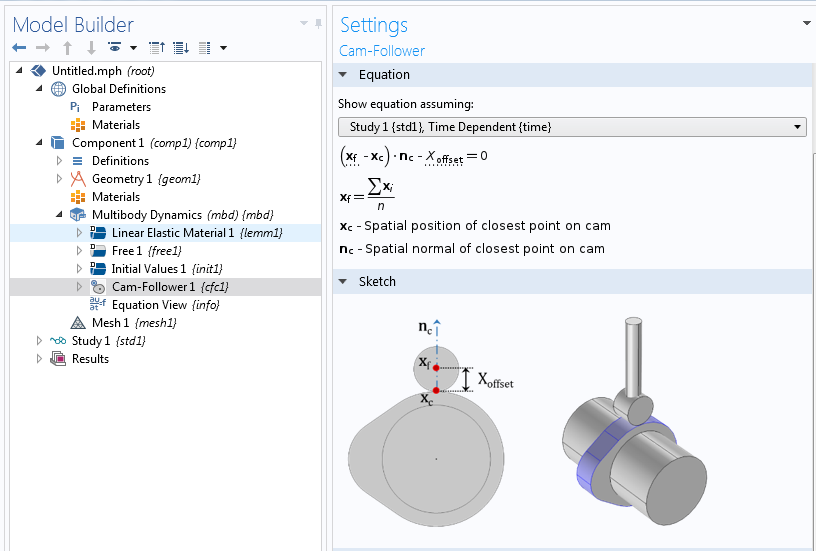
The Equation and Sketch for the Cam-Follower feature in COMSOL Multiphysics with the add-on Structural Mechanics Module and Multibody Dynamics Module.
If you are not interested in the details of the formulation, you can skip to the next section.
To understand the formulation, let’s take a look at an example of a cam and roller configuration in which both the cam and roller have been modeled as rigid components. For a rigid body, a point on the body can be located from the origin of a body-fixed (local) coordinate system (X, Y) by \vec{s}. Since the point is fixed to the body, the elements of the vector are constant in the body-fixed coordinate system, while in the global coordinate system, they vary with the rotation. The transformation from a local to global orientation is represented in terms of the rotation matrices.
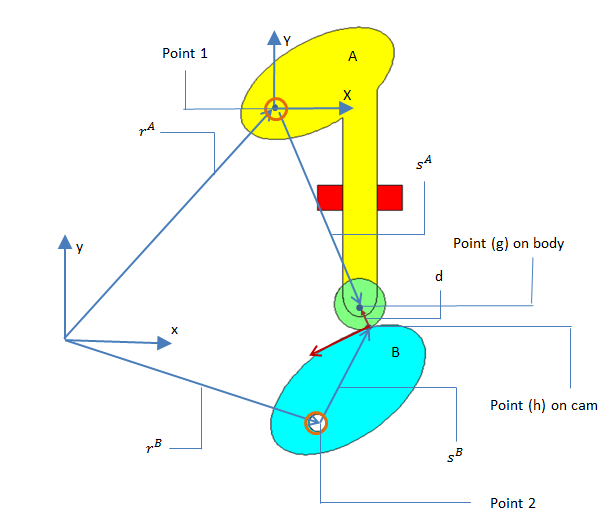
Schematic of the cam and roller configuration.
Now, the absolute position of point (P) on body (i) can be represented as follows:
Here, the position of point (c) is computed using the center of rotation of the rigid body and it also serves as the origin for the body-fixed coordinate system.
- x = Global x-axis
- y = Global y-axis
- rA = Absolute position of the center of rotation of body A
- sA = Global position vector for point (g) on body A with respect to the center of rotation
- rB = Absolute position of the center of rotation of body B
- sB = Global position vector for point (h) on body B with respect to the center of rotation
- RA = Absolute position of point (g) with respect to the spatial coordinate system
- RB = Absolute position of point (h) with respect to the spatial coordinate system
So,
As the common contact point is not fixed with respect to the bodies (A) and (B), a constraint needs to be defined between the two bodies to maintain continuous contact.
In COMSOL Multiphysics, the constraint is defined on the vector d such that its magnitude in the normal direction of the closest point on the cam surface is equal to the offset value.
Modeling a Radial Cam-Based Valve-Opening Mechanism
For our example, let’s consider a spring-loaded valve-opening mechanism that has a rocker arm and a radial cam. In this mechanism, the cam rotation is prescribed and a spring is attached to the valve to restrict its motion.
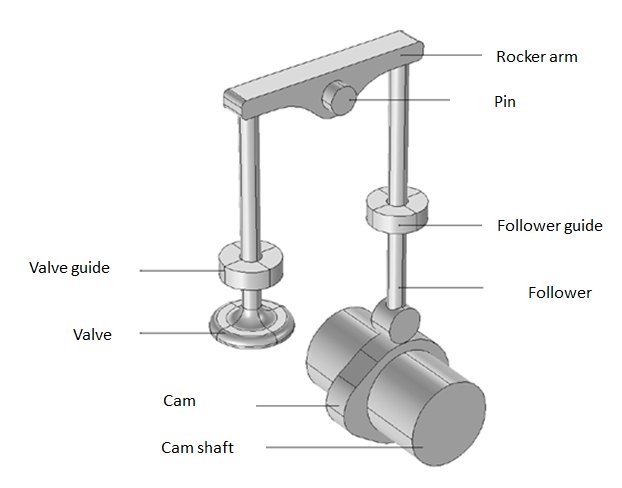
Geometry of a valve-opening mechanism with a rocker arm and radial cam.
The objective of this analysis is twofold:
- To compute the displacement, velocity, and acceleration of the follower for a given cam shaft RPM
- To compute the cam-follower connection force as well as the torque required to rotate the cam shaft at a given RPM for different values of valve spring stiffness
One of the main objectives behind mounting the spring on the valve is to force the follower to follow the cam profile and to avoid intermittent contacts between the cam and follower. Hence, the optimal value of the valve spring stiffness should enforce the contact between the cam and follower at all times, while simultaneously requiring the least torque to rotate the cam shaft.
Evaluating the Simulation Results in COMSOL Multiphysics®
Animation showing a displacement plot of the radial cam.
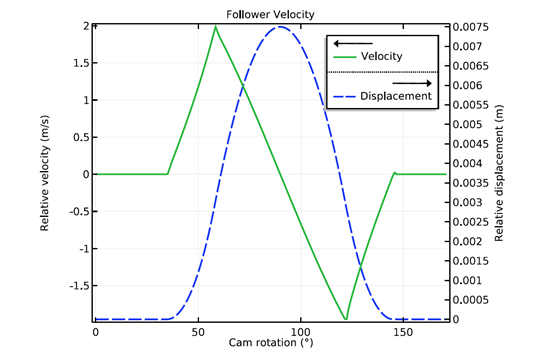
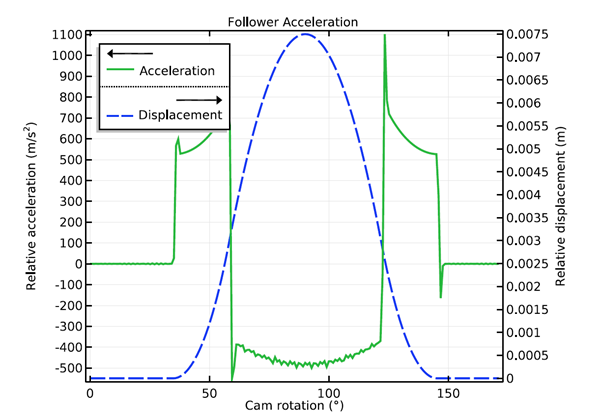
The follower velocity first increases when the follower comes in contact with the opening flank region of the cam profile. Later, it decreases and becomes zero at the tip of the nose region. Similarly, it increases in the reverse direction and becomes zero when the follower comes in contact with the heal region of the cam profile. In COMSOL Multiphysics, the joint’s velocity and acceleration sign convention is decided based on the specified axis of the joint. It will be positive if the destination attachment is moving along the positive direction of the axis of the joint. For this case, the joint axis is defined along the z-axis, so the velocity is positive when the follower is moving upward and vice versa.
Variation of the follower velocity (left) and follower acceleration (right) with cam rotation.
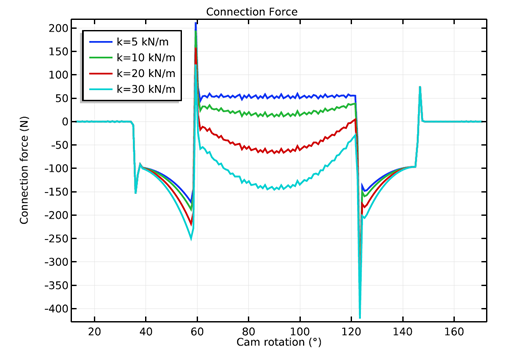
You can see that the acceleration values are negative in the range of 60° to 120° of cam rotation. This is the region where the follower has a tendency to leave the contact with the cam profile, which depends on the valve spring stiffness value for a given camshaft RPM. By plotting the connection force vs. cam rotation, you can check which spring ensures continuous contact. The contact force sign convention is positive if the cam and follower are no longer in contact, while the negative value shows that the contact is still maintained.
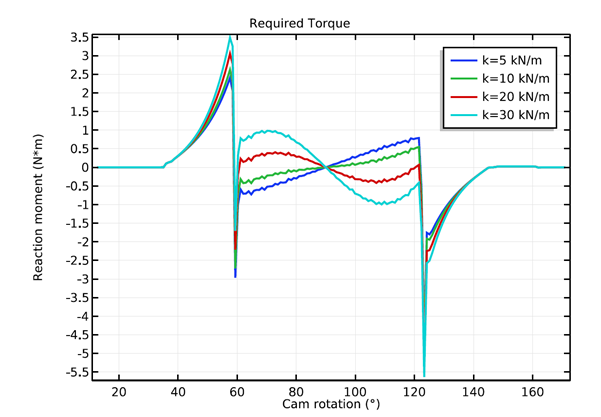
Variation of the cam-follower connection force with cam rotation (left) and torque required to rotate the cam shaft (right) for different values of the valve spring stiffness.
Out of the four valve stiffness values, only 20 kN/m and 30 kN/m can enforce a continuous contact between the cam and follower. To choose the optimal value of valve stiffness, we can look at the required torque plot. It can be observed in this plot that the required torque is less for a value of 20 kN/m, hence this is the optimal value of the valve stiffness among the values considered in this analysis.
Designing a Cam Profile Using the Known Follower Rise Function
One problem with cam design is to determine the cam profile suitable to generate the desired motion of follower. In COMSOL Multiphysics, one can easily create a geometry based on the follower rise function. The follower rise function is defined as the displacement of the follower with change in the cam rotation. The first step is to derive the radius as a function of the follower rise function. This relationship can be established using the analytical approach if the follower rise function is preknown. The analytical approach is quite simpler than the graphical approach of creating the cam surface, because the follower rise function is usually a combination of different elementary functions. Also, in a few cases, the desired output motion of follower is already known so it became simple to generate a cam profile from the known follower rise function.
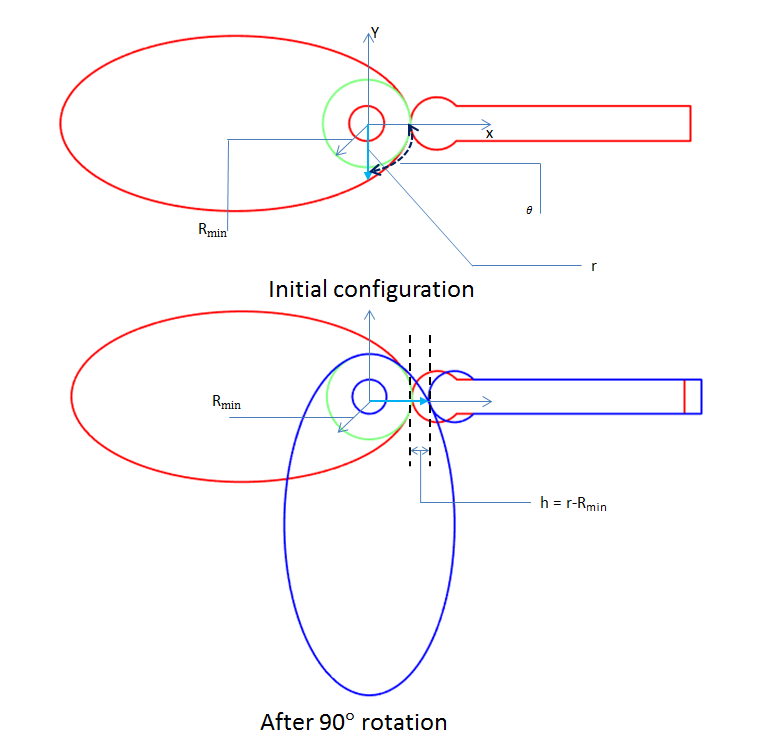
Schematic representing the variation of the cam profile with the cam angle.
- Rmin = Radius of base circle
- θ = Angle of rotation of points on the cam surface
- r = Radius of points on the cam surface
- h = Height of the follower above its initial position
From the above image, it is clear that the radius (r) and follower height (h) are functions of the angle of rotation and the follower rise function is simply a difference of cam profile from the base circle. The relation between them is defined as follows:
Now, if the follower rise function is known, the variation of the radius (r) will represent a circle for each value of θ. So, it will give a family of curves. In order to generate the cam profile, we need to plot the envelope of the curves. This can be easily done in COMSOL Multiphysics using the Parametric Curve option.
y=r\boldsymbol{\cdot}sin(\theta)
Let’s take a simple example to illustrate this concept. Consider a simple knife edge radial follower with a known follower rise and a cam angle rotation. The rise function is such that there is outstroke during 60° of cam rotation, dwell for the next 30° of cam rotation, return stroke during the next 60° of cam rotation, and dwell for the remaining 210° of cam rotation.
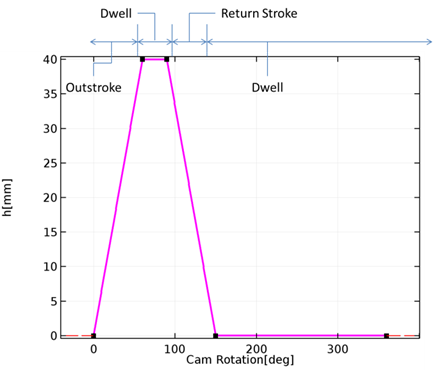
Follower height as a function of the cam angle. (Follower rise function.)
Implementation in COMSOL Multiphysics®
First, you need to create the interpolation function and enter the data for h vs. θ, also called the follower rise function. Thanks to the flexibility of the COMSOL® software, one can directly import the follower rise function. After importing the follower rise function, the cam surface can be generated using the parametric curve. For this, one needs to first determine the base circle radius and then express the radius that depends upon the follower rise function and base circle radius. The parametric form is similar to that of a circle; the only difference in this case is that the radius is a function of θ. To do this in COMSOL Multiphysics, one can use the interpolated function to create the follower rise function and further use them under the parametric curve to define the value of r (the radius of the cam surface). Usually, the data is a piecewise curve, so it is good practice to create different profile curves for each section of outstroke, upstroke, and dwell. Finally, you use the Convert to solid option to generate the cam profile.

Schematic of the generated cam profile.
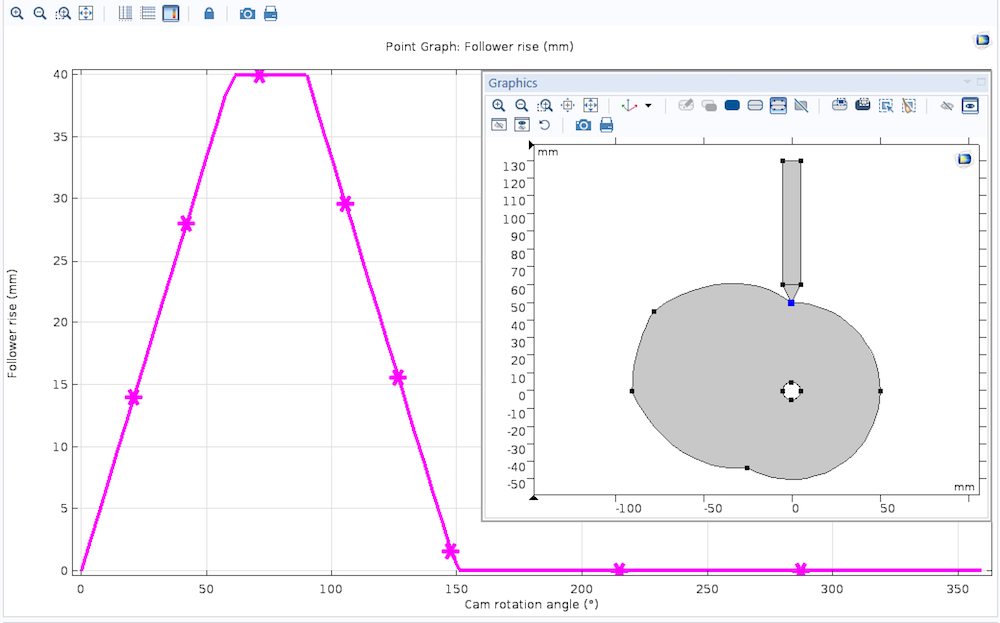
A plot of the follower rise as a function of the cam rotation, after performing a simulation with the generated cam profile.
The cases in which the motion of the follower is a combination of different types of analytical expressions, such as uniform motion, parabolic motion, simple harmonic motion, cycloidal motion, or general polynomial motion. In these cases, the cam profile can be easily created using the Analytic Function feature with a combination of different motions for the full cam rotation. The analytic function allows a symbolic expression, so you can directly write it as a function of θ.
Final Notes About the COMSOL Multiphysics Implementation
In order to get a smoother surface representation, it is useful to increase the shape function order for the displacement to Quadratic. This applies both when the cam is rigid and when it is flexible.
If possible, use a fine mesh on a cam boundary to improve the accuracy of the mesh normal used in the Cam-Follower connection node.
Next Step
The Structural Mechanics Module contains advanced tools for mechanical analyses. See what other types of analysis are possible by clicking the button below.
Note: The Cam-Follower feature also requires the Multibody Dynamics Module, an add-on to the Structural Mechanics Module.






Comments (0)