
The Rotating Machinery, Magnetic physics interface available in the AC/DC Module is used to model rotating machines such as motors or generators. When modeling the linear or tubular device with the Magnetic Fields and the Moving Mesh physics interfaces, it is appropriate to use a customized linear periodic boundary condition. In this blog post, we will explore how to customize the linear periodic boundary condition and model the tubular generator that is used for wave energy.
Linear Electric Motors or Generators
A linear electric motor (LEM) is an electromechanical device that produces linear motion without using any mechanism to convert rotary motion to linear motion. LEMs are similar to rotary motors, whose stator and rotor have been cut along a radial plane and unrolled to provide linear thrust. The same electromagnetic force that produces torque in a rotary motor generates a direct linear force in a linear motor.
It is worth mentioning that the Rotating Machinery, Magnetic interface available in the AC/DC Module includes all of the features that are needed to model a rotating machine. This interface is a combination of the Magnetic Fields interface; the Magnetic Fields, No Currents interface; and the Moving Mesh interface. It is customized for modeling rotating machines and greatly simplifies the definitions of the stationary and rotating domains and the handling of the interfaces between them. Features like sector symmetry and periodic boundary conditions are also extremely useful for modeling a sector or portion of the model to obtain results for the whole device. Although this interface significantly reduces the effort required to set up a model of rotating motion, we cannot use it for linear motion.
Today, we will demonstrate how to model a tubular generator using the customized coupling of the Magnetic Fields and the Moving Mesh physics interfaces. Additionally, we will explain how to create the linear periodic boundary condition — an essential element for modeling linear/tubular motors or generators with the General Extrusion operator.
Tubular Generators for Wave Energy Conversion System
Tubular machines have been considered in numerous applications, from active vehicle suspension systems to tidal and wave energy conversion systems. The transmission efficiency of tubular machines is greater than conventional linear and rotary conversion systems, as the thrust force acts directly on the load. Another advantage of tubular machines is that they have no stator-end windings. Thus, the copper losses are relatively low and the utilization ratio of permanent magnet materials is high.
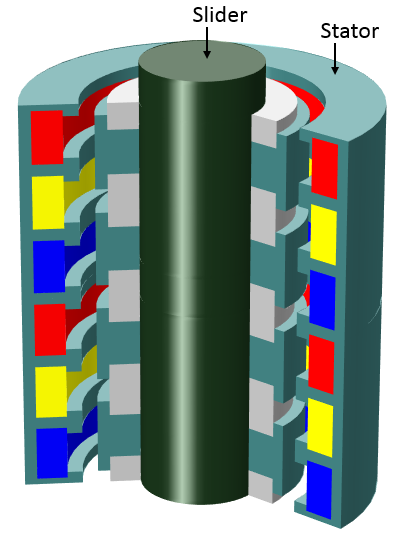
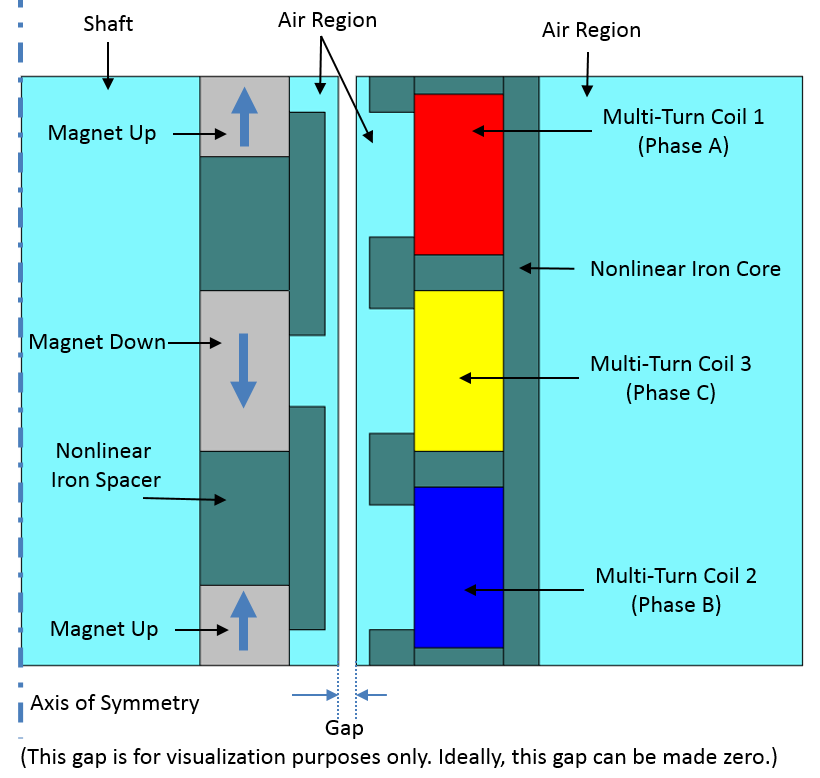
Here, we will discuss the technique for modeling a tubular generator (illustrated below). The tubular generator consists of two major parts: a stationary stator and a linearly moving slider. The stator is comprised of three-phase windings and a nonlinear magnetic core. The slider consists of a shaft, permanent magnets, and nonlinear magnetic material between the permanent magnets.
Left: A 3D view of the tubular generator. Right: A 2D axisymmetrical view of the tubular generator. This view details the arrangements of the coils, the permanent magnets, and the nonlinear magnetic material.
Modeling a Tubular Generator with COMSOL Multiphysics
Using the Magnetic Fields and the Moving Mesh physics interfaces, we can model the tubular generator described above in COMSOL Multiphysics. The model is set up in the 2D axisymmetry domain, as the model is symmetric around the machine’s axial axis. The geometry is fully parameterized, enabling the model’s use in optimization or parametric sweep studies, if needed. The parameters are defined under Global Definitions > Parameters, as shown in the screenshot below. You can download the tubular generator example presented here from our Application Gallery.
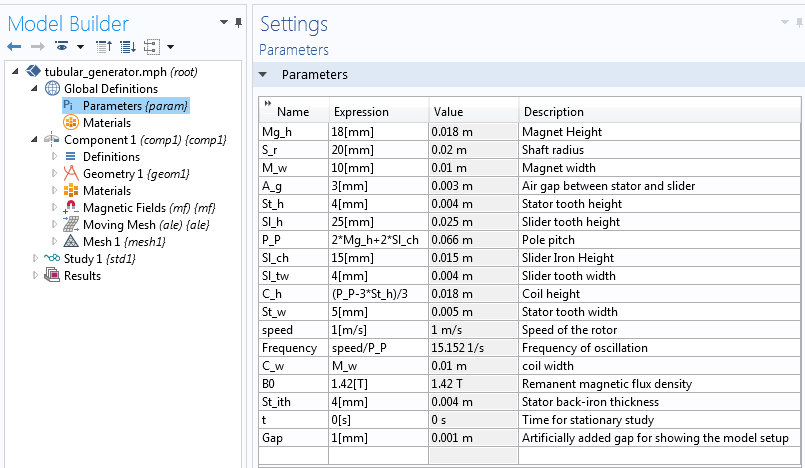
A list of parameters that are used to set up the tubular generator model.
The model geometry is designed so that the stator part and the slider part are created as separate unions. These parts are then finalized with the Form Assembly so that the identity pair is automatically created between the stator and the slider in the interface. The moving mesh is also added in order to model the slider’s movement.
Note: Here, we have added an extra gap of 1 mm between the stator and the slider. This makes the overlapping boundaries visible so that we can apply the customized linear periodic boundary condition. The gap is purely for visualization purposes and does not have any effect on the results (i.e., the voltage output or the electromagnetic forces).
Physics I: Magnetic Fields
The Magnetic Fields interface is used to model the tubular generator’s electromagnetic field. The nonlinear material in both the stator and the slider is modeled using the Ampère’s Law node, with a constitutive relation set to an H-B curve.
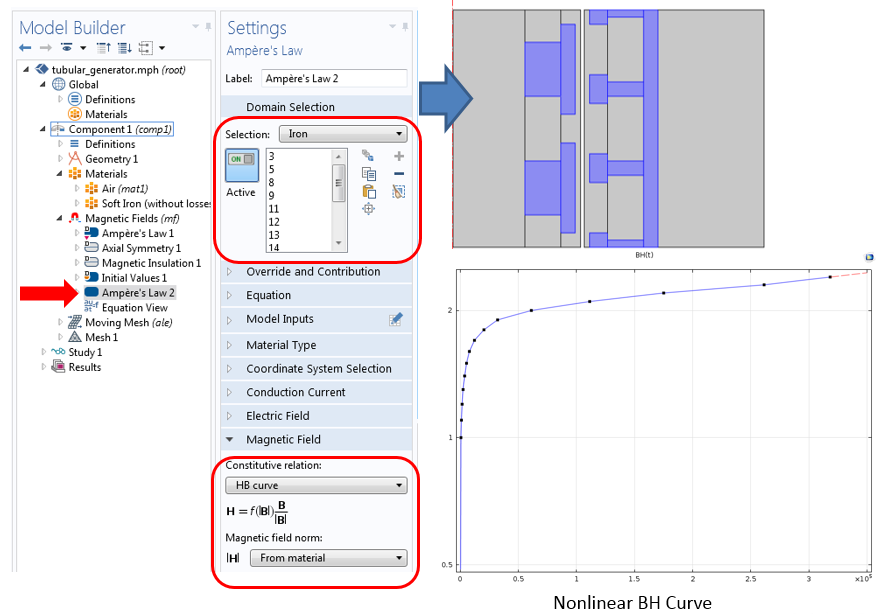
The settings for the Ampère’s Law node, illustrating H-B curve implementation in the nonlinear magnetic regions.
The three-phase windings are modeled in the Magnetic Fields interface using the Multi-Turn Coil feature. All three phases have the same settings. Only the settings for the third phase are shown below. Each phase winding consists of 100 turns of wires with a cross-sectional area of 1e-6[m^2] and an electrical conductivity of 6e7 s/m. All phases are set as an open circuit (i.e., zero currents) so that the induced voltage in the coils can be computed.
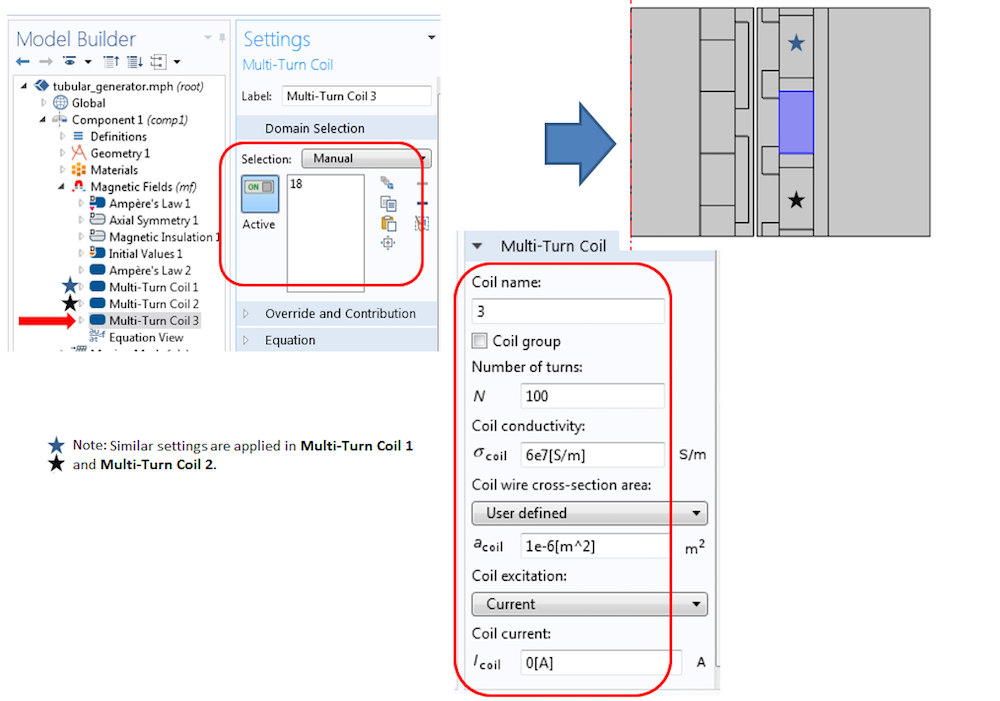
The Multi-Turn Coil feature shows open circuit settings as well as the number of turns, conductivity, and a cross-sectional area.
The permanent magnets in the slider are modeled using the Ampère’s Law node, with the constitutive relation set to the remanent flux density. Two separate nodes are added for a magnet pointing upward and a magnet pointing downward. Only the settings for the magnet pointing downward are illustrated below.
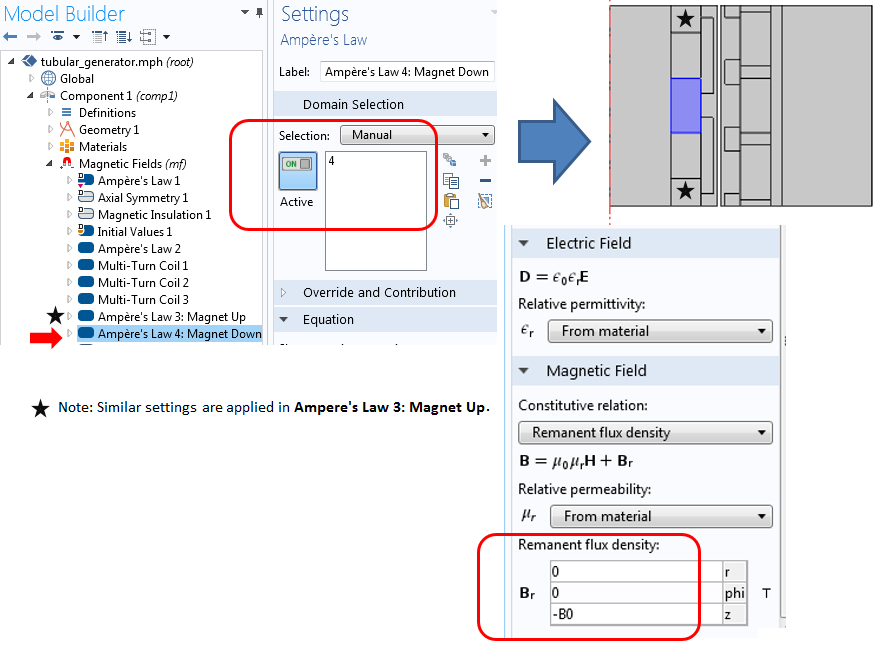
The settings for an Ampère’s Law node showing the permanent magnet.
Since we are only solving a section of the tubular generator, we must apply appropriate periodic boundary conditions on either ends of the stator and the slider. Here, the appropriate periodic condition is a continuity condition.
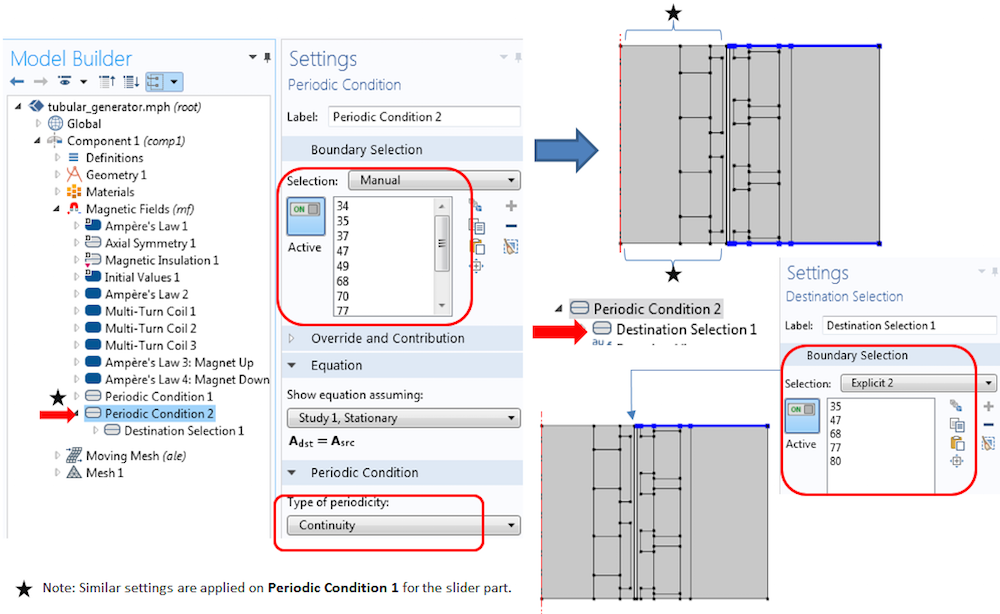
The continuity periodic boundary condition settings in the stator side. A similar setting is also used for the slider.
Customizing Linear Periodic Boundary Conditions
The Rotating Machinery, Magnetic interface already contains the Sector Symmetry feature. This feature is useful for simply modeling a sector of a rotating machine, while still ultimately obtaining the results for the full device. Note that the Sector Symmetry feature is only applicable for rotating machines, not for linearly moving motors or generators.
To build such customized linear periodic boundary conditions, you will need to perform a few extra steps. To begin, you must create the sawtooth waveform with the same angular frequency as that of the generator. You can do so under Component 1 > Definitions > Waveform 1. In the screenshot below, additional settings for the sawtooth waveform are shown.
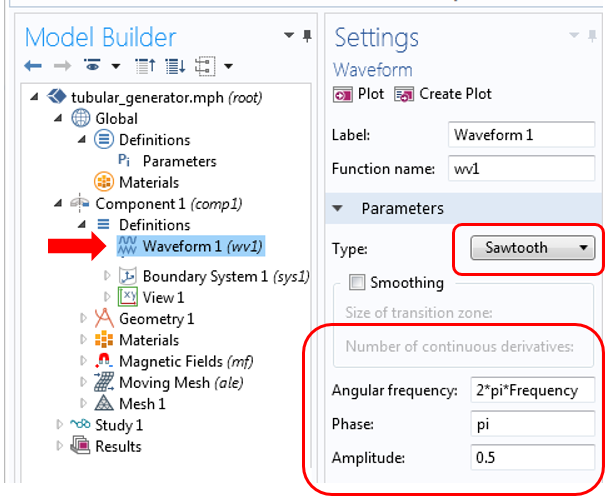
Settings for the sawtooth waveform when modeling the angular frequency of a generator.
The sawtooth waveform added above is used to create an analytic function that is similar to the sawtooth waveform but offset by an amplitude of 0.5. The analytic function is added under Component 1 > Definitions > Analytic 1.
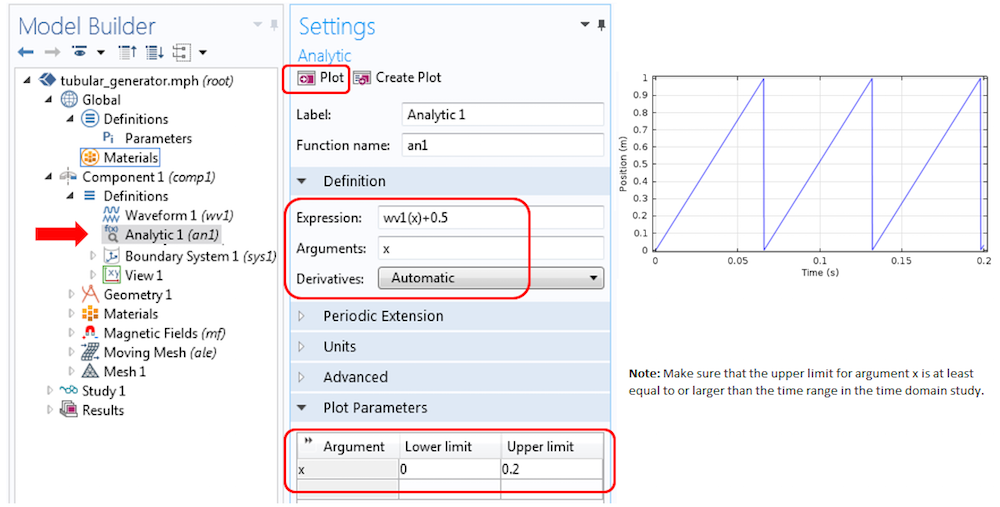
Settings for the analytic waveform and the resultant waveform plot.
At the identity pair — a common boundary between the stator and the slider — we should impose continuity of the dependent variable (vector potential, Az). Since the stator is stationary and the slider is moving with a certain frequency, we need to customize this continuity condition to reflect the linear periodicity both in the stator and the slider. To do so, you can use General Extrusion operators to map the fields from the stator to the slider.
The stator boundary 33 is used as the source boundary in the General Extrusion operator. Additional settings are shown below.
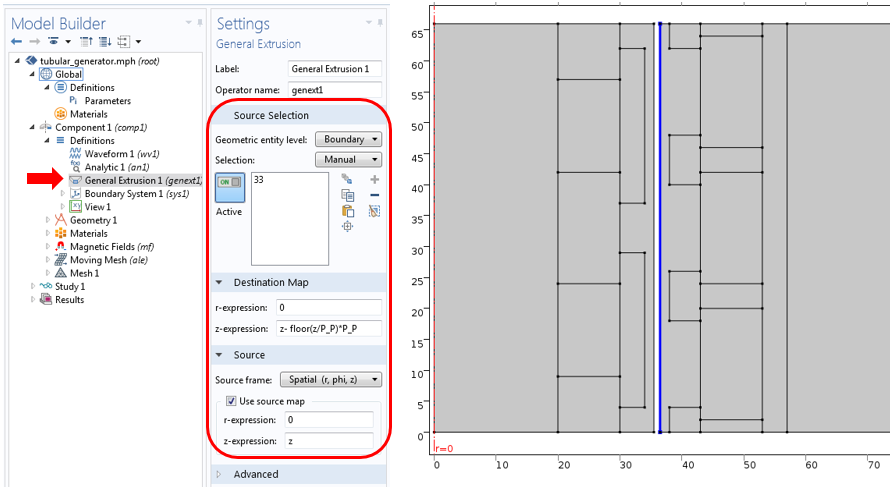
Settings for the General Extrusion operator defined on the stator boundary. Only the data in the z-expression is mapped.
Now we are ready to apply the periodic continuity boundary condition on the common boundaries. To make this happen, we need to map the vector potential from the stator boundary to the slider boundary. Adding the Magnetic Potential boundary condition on boundary 32 enables this.
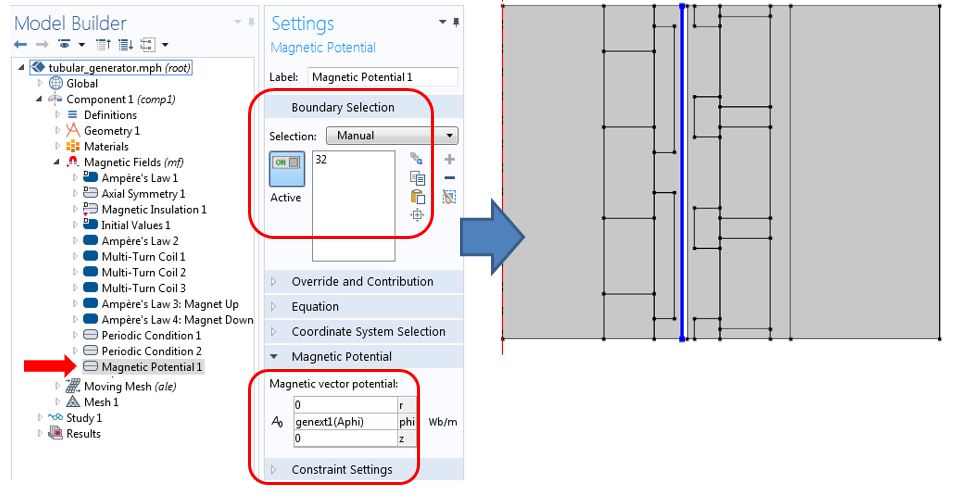
The mapping of vector potential from the stator boundary to the slider boundary using the General Extrusion operator.
To complete the electromagnetic modeling, we need to apply the Perfect Magnetic Conductor boundary condition on the stator boundary. This is done because the default boundary condition (Magnetic Insulation) is incompatible with the magnetic continuity that we want to achieve. On the other hand, the Perfect Magnetic Conductor boundary condition is a homogeneous Neumann condition and will, in this context, provide flux continuity.
For details, please see a previous blog post on the weak form.
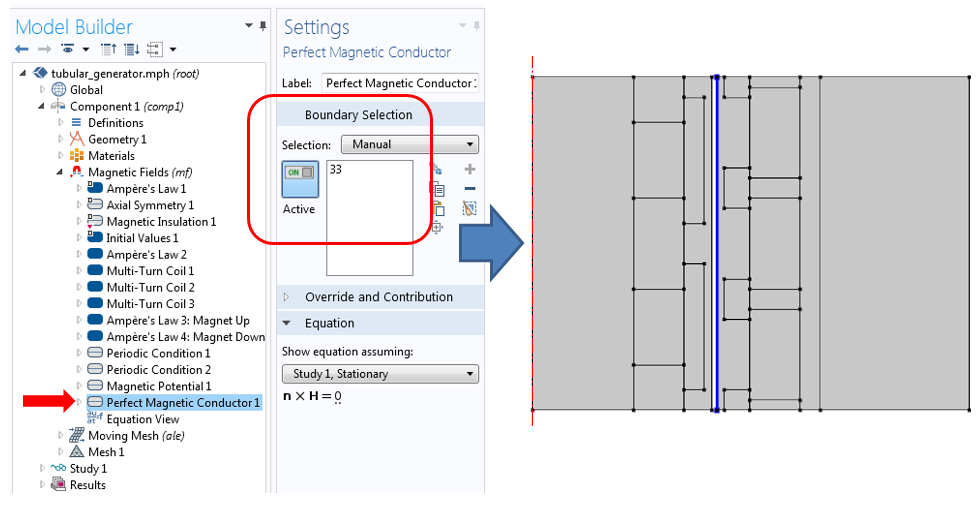
Settings for the Perfect Magnetic Conductor boundary condition on the stator boundary.
Note: To model any linear machines (i.e., linear induction or synchronous motors/generators), you can customize the continuity boundary condition that enforces the linear periodicity using the same technique discussed here. While this approach will work for 2D and 2D axisymmetry geometries, it will be more complicated for 3D geometries. We will not discuss customized 3D linear periodic boundary conditions in this blog post.
Physics II: Moving Mesh
To model the linear motion, we can begin by adding the Moving Mesh interface. The stator domains (and the air region on the side) are assigned a fixed mesh. The slider part, meanwhile, is modeled using the prescribed deformation in the z-direction, with a prescribed motion defined by the previous analytic function.
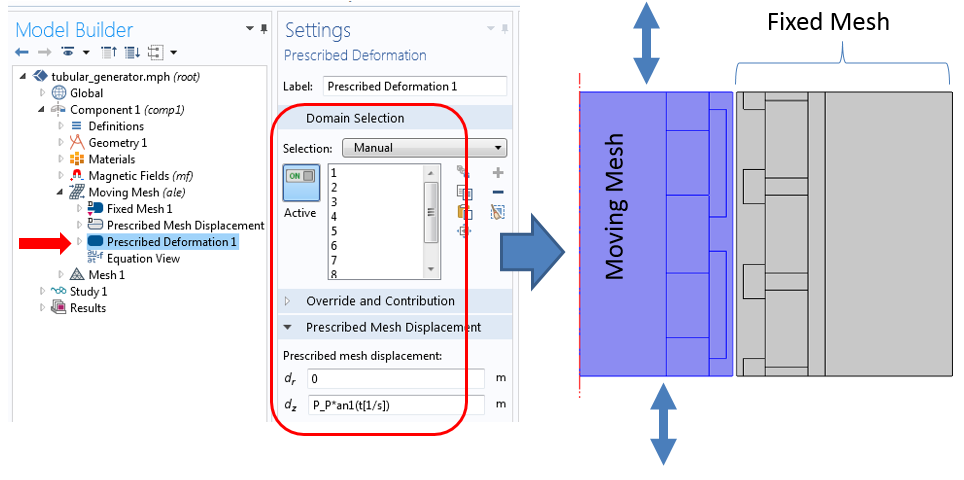
The Moving Mesh physics interface and its associated feature settings for modeling a tubular generator.
Meshing: In the edges where the periodic boundary conditions are applied, the source and destination edges should have the same meshes. The Copy Edge feature is applied to ensure this. Additionally, the General Extrusion operator is used to apply the finer mesh in the boundaries where the manual continuity boundary condition is set up.
Solver Settings and Results
There are couple of things that you need to remember in order to set up the correct solver for your simulation. First, you need to add a Stationary study step to compute the vector potential field inside and around the stationary permanent magnet. Using this stationary solution as the initial condition, you can then solve a Time Dependent study step. This step computes the transient response resulting from the linearly moving slider and the induced voltage in the three-phase coils. Because the problem is solved in the time domain and since a nonlinear magnetic material is included in the model, we must slightly tune the nonlinear time-dependent solver. The nonlinear solver setting is similar to the one suggested in this knowledge base entry.
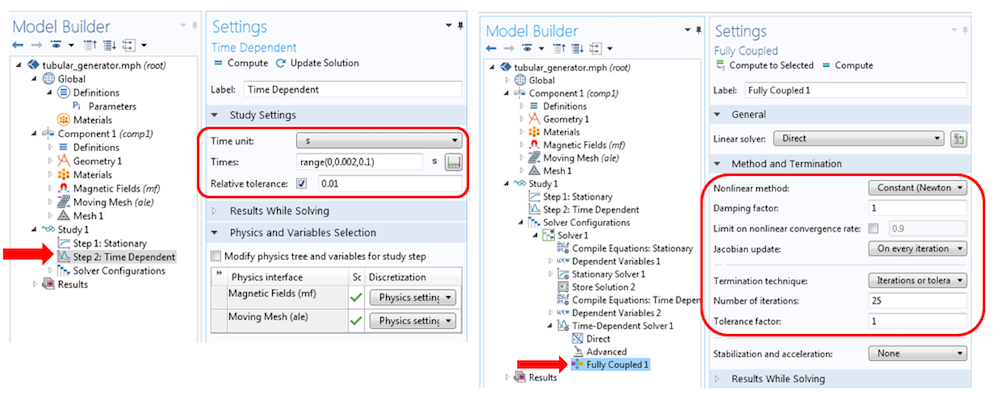
The nonlinear solver settings for a tubular generator. The model is solved for 0.1 s.
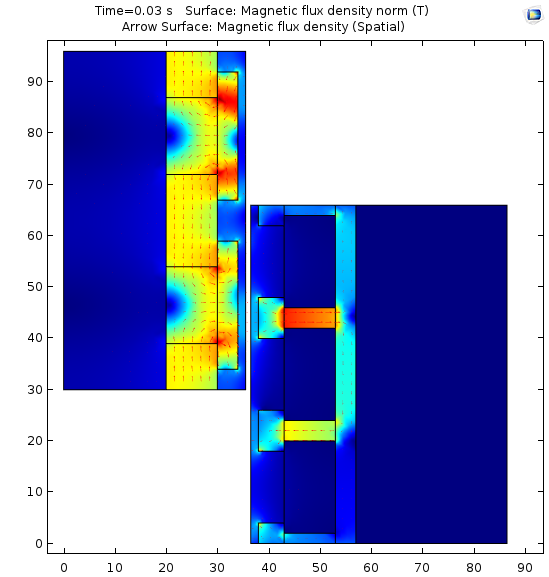
Left: A 2D axisymmetry surface and arrow surface plot of the magnetic flux density at t=0.03 s. Right: A magnetic flux density surface plot on the revolved 3D geometry at t=0.1 s.
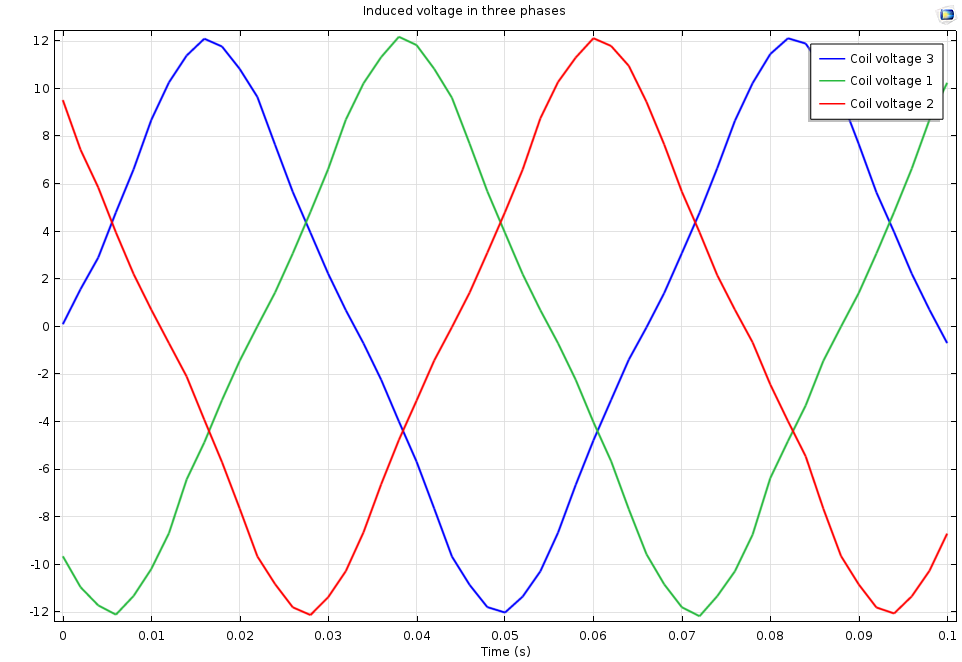
Open circuit induced voltages in three-phase stator multi-turn windings as a function of time.
Summary
The existing Rotating Machinery, Magnetic interface is the solution for modeling rotating machines. However, when modeling linear or tubular machines, it is more appropriate to use the Magnetic Fields and the Moving Mesh physics interfaces.
Here, we have demonstrated how to customize the linear periodic boundary conditions using General Extrusion operators as well as how to model the tubular generator that is used for wave energy generation. The same technique that we have presented today can also be used to model many classes of linear machines.
Try It Yourself
- Download the tutorial model: Tubular Permanent Magnet Generator







Comments (12)
priya jaspal
October 23, 2015Hi,
If I want to calculate various losses generated and thus efficiency of this generator, how that can be done in this software?
I am new to comsol. Would really appreciate your help
Nirmal Paudel
November 20, 2015Hi Priya,
Various losses such as resistive loss (copper loss), inductive loss (eddy current loss) can be calculated in Magnetic Fields, Magnetic and Electric Fields or Rotating Machinery, Magnetic physics interfaces. For hysteresis losses, you could either include the complex permeability of the material or add extra equations to include, for example, Jiles Atherton Hysteresis model in COMSOL. You might want to contact COMSOL Technical Support for relevant examples.
Best Regards,
Nirmal
Ruslan Lagashkin
February 1, 2016Hello,
I a modelling an asynchronous motor. How is it possible to apply voltage to the coils?
I know the physical dimensions of the motor, as well as resistance, inductance and mutual capacitance of the coils.
Also, if there is a tutorial about asunchronous motor modelling, or similar, it might be useful.
Thank you and Best regards,
Ruslan
Nirmal Paudel
February 19, 2016Hi Ruslan,
For an asynchronous motor, you could use the Multi-Turn Coils features as shown in this blog post, but instead of a zero current setting, you would apply a voltage excitation.
The physical dimensions of the motors is needed to construct the geometry with all the necessary parts, for examples, coils, cores, etc. You do not have to input the resistance or inductance or capacitance values of the coil, but the software will determine that based on your geometry of coils, material properties, separation between coils etc. However, if you are modeling a motor in 2D and would like to include these parameters to take into account the effects of 3D, you may do so by adding the Electrical Circuit interface to the Finite Element model of the motor.
Unfortunately, we do not have any example to demonstrate this at this point for the motor or generator. But the coupling of finite element model with circuit is done in several examples below:
http://www.comsol.com/model/inductor-in-an-amplifier-circuit-990
http://www.comsol.com/model/transient-modeling-of-a-capacitor-in-a-circuit-12695
Best Regards,
Nirmal
Israt Jahan
December 2, 2016Hi
I am trying to calculate induced voltage in one slot in my PMSM 2D motor in open circuit. I used your instruction to put (icoil=0) in multi turn coil. But i did not get the sinusoidal voltage output like you. Is there any way to send my model to you ? So you can look at the model or i will send it to comsol support.
BR
Israt
Caty Fairclough
December 5, 2016Hello Israt,
Thank you for your comment.
For questions related to your modeling, please contact our support team.
Online support center: https://www.comsol.com/support
Email: support@comsol.com
Best,
Caty
Nicola Barlabà
December 13, 2016Hi
i’m trying to modeling a linearized axial flux permanent magnet motor. What i need to simulate is the moving of 2 external rotor, and to do this i follow this tutorial to set boundary periodic condition. I’m using “moving geometry” physic. What happen when i give a prescribed mesh displacement is that the rotor isn’t treated as being of infinite length. Since I have not been able to find anything that explains how periodize the rotor, I tried to set the displacement mesh as a periodic analytic function. the problem is that the analytical function of saw tooth has a discontinuity and the solver does not converge. What should i do? Thank you
Bridget Cunningham
December 22, 2016Hello Nicola,
Thank you for your comment.
For questions related to your modeling, please contact our support team.
Online support center: https://www.comsol.com/support
Email: support@comsol.com
Best,
Bridget
luca spadoni
February 19, 2017Which module for smr motor?thanks
Caty Fairclough
February 21, 2017Hi Luca,
Thanks for your comment! This was done with the AC/DC Module.
If you have further questions, please feel free to reach out to our support team.
Online support center: https://www.comsol.com/support
Email: support@comsol.com
Best,
Caty
Brahim Hiba
March 30, 2017dear Nirmal
thank you for the great article
i wour on the same model like you con would you please ask me how to build the three phase coil (Linear Motors) in comsol multy physics 5.2
thank you
best regards
brahim
bruno laurella
May 15, 2018Dear Nirmal
You have some idea of how you could visualize the induced currents in the coils in this model.