
One of my favorite sitcoms is “The Big Bang Theory”, thanks to its focus on physics. From time to time they run funny experiments that can be easily arranged at home, causing me to wonder if I know the physics that are at work. One of my favorite episodes is when they fill the cone of a speaker with a suspension of starch in water. Instead of spattering around, the suspension starts to dance because it behaves more like a solid than a fluid under the percussive action of the speaker’s cone. Non-Newtonian fluids are another fascinating counter-intuitive effect to study.
Materials Between Solids and Fluids
Solids deform under an applied stress and reach a position of equilibrium in which their deformation ceases. When the stress is removed, they will go back to their original shape. On the contrary, fluids deform continuously and don’t retain any particular shape. In scientific terms, we say that solids are characterized by elasticity while fluids are characterized by viscosity.
In between these two extremes lie non-Newtonian fluids, exhibiting both elasticity and viscosity. A suspension of starch in water belongs to this broad class of fluids and can be further classified as shear thickening: its viscosity increases with increasing shear rate. Another example of shear thickening fluid is sand soaked in water. The material dancing on a speaker’s cone on the TV show must therefore have been a non-Newtonian fluid.
Have you ever painted?
If the answer is yes, I’m pretty sure you noticed that the shear created by the brush made the paint thin and capable of wetting out the wall surface evenly. Once applied, the paint regained its original higher viscosity, leaving your wall without drips and runs. This is what is called a shear thinning fluid, the exact opposite of shear thickening. Can you recall other fluids exhibiting a non-Newtonian behavior?
Simulating Non-Newtonian Fluids
When looking to simulate non-Newtonian fluids, one example that comes to mind is the injection molding of a polymer. A ready-to-run model is available to download from the Model Gallery. I suggest starting from this model if you’re interested in simulating non-Newtonian flows. Below are a few images highlighting the shear thinning behavior of this polystyrene solution flowing into a mold.
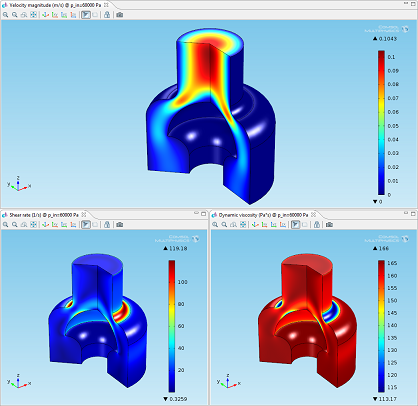
In this model the polystyrene solution is flowing into the mold from the top to
the bottom. Results show how for a shear thinning fluid, the dynamic viscosity is
lower when the shear rate is higher. Top: velocity magnitude. Bottom left: shear rate.
Bottom right: dynamic viscosity.
|
|
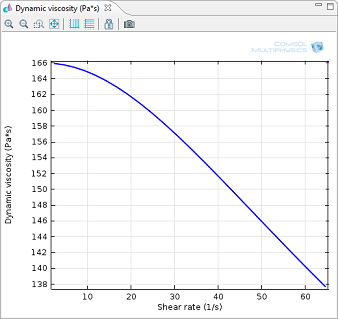
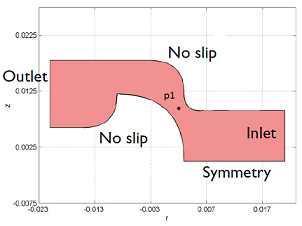
Dynamic viscosity as a function of shear rate. Values are measured in p1.
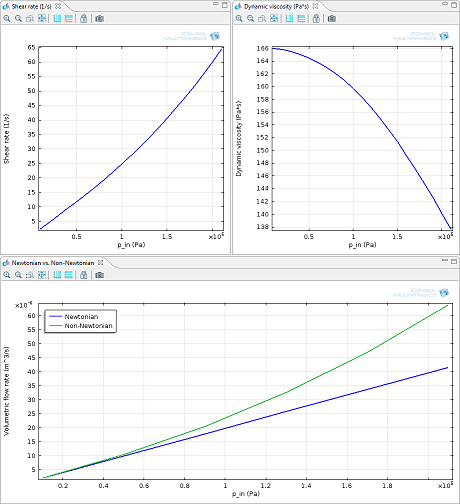
Top left: shear rate as a function of inlet pressure. Top right: dynamics viscosity as a
function of inlet pressure. Values are measured in p1. Bottom: comparison between the
non-Newtonian polystyrene solution and an equivalent Newtonian fluid. As expected, the
volumetric flow rate is higher for the polystyrene solution since at higher shear rates its
viscosity is lower.






Comments (6)
Ben salah Cherif
January 22, 2013Thank you for this information and I really love the part of Big ban theory 🙂
Daniel Grivon
December 8, 2013Hi Valerio,
I am really interested in the example you posted because I want to simulate the non-newtonian fluid behaviour for Bingham fluid using the Bingham-Papanastasious model, but to compute the shear dependent viscosity for a given point I need to obtain the shear rate value at that point.
How have you computed the shear rate at point p1?
Considering that the model is two dimensional axisymmetric did you define the shear rate as du/dr, where u is the velocity profile and r is the radial coordinate?
Thank in advance for you reply
Valerio Marra
December 10, 2013Hi Daniel,
Great questions! I’ll try to answer to all of them.
Q: I want to simulate the non-newtonian fluid behaviour for Bingham fluid using the Bingham-Papanastasious model, but to compute the shear dependent viscosity for a given point I need to obtain the shear rate value at that point.
A: All physics nodes in the model tree introduce predefined variables that can be usually used throughout the model. They’re typically functions of the dependent variables and their derivatives.
Display the Equation View subnode in the model tree to access them: click the Show button and select Equation View from the Model Builder. Click the Equation view subnode and the corresponding settings window will show you detailed information about the implementation of each physics feature, such as the variables.
Let’s take a look at the Fluid Properties node: it defines a variable that from its expression, description, and unit of measure, I’d say it’s exactly what you’re looking for. It’s the shear rate!
COMSOL allows you you to type in your user defined dynamic viscosity expression based on such variable (and others, if needed). In the Fluid-Structure Interaction in Aluminum Extrusion model available in the Model Libraries (http://www.comsol.com/model/fluid-structure-interaction-in-aluminum-extrusion-4386) we show how to do it.
Q: How have you computed the shear rate at point p1?
A: I’ve added this point to the geometry and once the model was solved, I’ve added to the Results branch a 1D Plot Group with a Point Graph.
Q: Considering that the model is two dimensional axisymmetric did you define the shear rate as du/dr, where u is the velocity profile and r is the radial coordinate?
A: Once you select the space dimension of your model, COMSOL will take care of the underlying mathematical formulation. You don’t have to worry about it but, if you’re really curious, you now know the trick: take a look under the hood with the Equation View subnode.
I hope you’ll find my answers useful.
Happy multiphysics simulation!
Valerio
P.S. Many of these variables are available in the Predefined quantities lists in the settings for plots and other results nodes.
Wenjun Yuan
January 2, 2015In my simulation, as the fluid acts on the solid, the solid is moving in the fluid. It was perfect in the Newtonian fluid. However, when it comes to the non-Newtonian fluid, it cannot preceed. I observed that the stress on the solid surface was illogical, How could this be? What do you think I am going to do with that?
Valerio Marra
January 2, 2015Hi Wenjun,
I’d need more information in order to help you, I suggest to contact my colleagues at support@comsol.com.
Best regards,
Valerio
Davin Christian Raharja
June 13, 2016Hi Valerio,
I’m working right now on non newtonian flow simulation in cores and want to plot shear rate vs viscosity. However, I can’t manage to plot it. Maybe could you help me ? I have used 1D plot group and changed the expression into dynamic viscosity and shear rate for y axes and x axes, respectively.
Thank you
Best Regards,
Davin