
Le logiciel COMSOL Multiphysics® propose plusieurs formulations différentes pour résoudre les problèmes d’écoulement turbulent : les modèles de turbulence L-VEL, yPlus algébrique, Spalart-Allmaras, k-ε, k-ω, k-ε bas Reynolds, SST et v2-f. Ces formulations sont disponibles dans le module CFD, et les modèles L-VEL, algébrique yPlus, k-ε et k-ε bas Reynolds sont également disponibles dans le module Heat Transfer. Dans ce billet de blog, découvrez pourquoi utiliser ces différents modèles de turbulence, comment choisir l’un d’entre eux et comment les utiliser efficacement.
Ce billet a été initialement publié en 2013. Il a depuis été mis à jour pour inclure tous les modèles de turbulence actuellement disponibles avec le module CFD à partir de la version 5.3 du logiciel COMSOL®.
Introduction à la modélisation de la turbulence
Commençons par considérer l’écoulement d’un fluide sur une plaque plane, comme le montre la figure ci-dessous. Le profil de vitesse uniforme frappe le bord d’attaque de la plaque plane, et une couche limite laminaire commence à se développer. L’écoulement dans cette région est parfaitement prévisible. Après une certaine distance, de petites oscillations chaotiques commencent à se développer dans la couche limite et l’écoulement et l’écoulement devient progressivement turbulent, pour finalement l’être complètement.
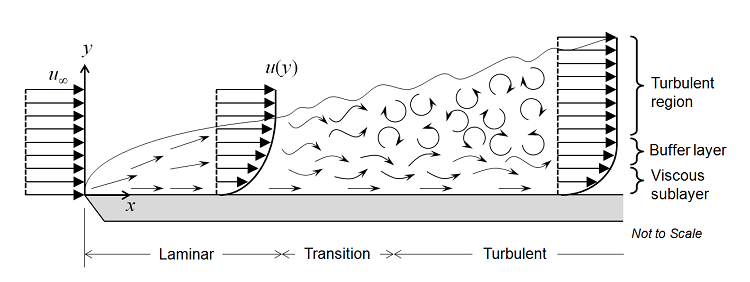
La transition entre ces trois régions peut être décrite par le Nombre de Reynolds, Re=\rho v L/\mu, où \rho est la masse volumique du fluide; v est la vitesse; L est la longueur caractéristique (dans ce cas, la distance depuis le bord d’attaque); et \mu est la viscosité dynamique du fluide. Considérons un fluide newtonien, ce qui signifie que les contraintes visqueuses sont directement proportionnelles au taux de cisaillement, la viscosité dynamique étant le coefficient de proportionnalité. C’est le cas, ou presque, pour un large éventail de fluides souvent utilisés en ingénierie, comme l’air ou l’eau. La masse volumique peut varier avec la pression, bien qu’ici nous considèrerons le fluide comme étant faiblement compressible, c’est à dire que le Nombre de Mach est inférieur à environ 0.3. L’option de faible compressibilité dans les interfaces d’écoulement de COMSOL Multiphysics® néglige l’influence d’ondes de pression sur l’écoulement et le champ de pression.
En régime laminaire, l’écoulement peut être complètement prédit en résolvant les équations de Navier-Stokes, qui donnent les champs de vitesse et de pression. Considérons tout d’abord que le champ de vitesse ne varie pas dans le temps. Un exemple de cela est illustré dans le tutoriel La couche limite de Blasius. Au fur et à mesure qu’il commence sa transition vers la turbulence, des oscillations apparaissent dans l’écoulement, malgré le fait que le débit d’entrée reste constant. Il n’est alors plus possible de considérer l’écoulement comme étant invariant dans le temps. Dans ce cas, il est nécessaire de résoudre les équations de Navier-Stokes temporelles, et le maillage utilisé doit être suffisamment fin pour résoudre la taille des plus petits tourbillons dans l’écoulement. Ce type de situation est illustré dans le tutoriel Ecoulement derrière un cylindre. Notez que dans ce modèle l’écoulement est instationnaire, mais toujours laminaire. Les problèmes d’écoulements laminaires stationnaires et temporels ne nécessitent aucun module et peuvent être résolus avec COMSOL Multiphysics® seulement.
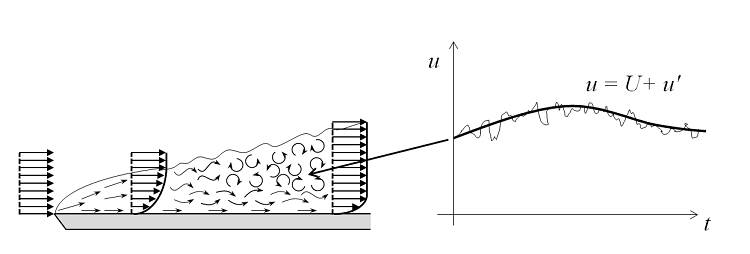
Lorsque le débit — et donc le nombre de Reynolds — augmente, l’écoulement révèle de petits tourbillons, et les échelles temporelle et spatiale des oscillations deviennent tellement petites qu’il est numériquement impossible de les résoudre en utilisant les équations de Navier-Stokes, en tous cas pour la plupart des cas pratiques. Dans ce régime d’écoulement, nous pouvons utiliser une formulation RANS (Reynolds-averaged Navier-Stokes), basée sur l’observation selon laquelle l’écoulement (u) dans le temps contient de petites oscillations locales (u’) et peut être traité comme une moyenne temporelle (U). Pour les modèles à une ou à deux équations, des équations supplémentaires de transport sont introduites pour les variables de la turbulence telles que l’énergie cinétique turbulente (k dans k-ε et k-ω).
Pour les modèles algébriques, les équations algébriques qui dépendent du champ de vitesse — et, dans certains cas, de la distance aux parois — sont introduites de façon à décrire l’intensité de la turbulence. A partir d’estimations des variables de turbulence, une viscosité turbulente est calculée, qui s’ajoute à la viscosité moléculaire du fluide. Le mouvement qui serait transmis par les petits tourbillons est à la place traduit en transport visqueux. La dissipation turbulente prime généralement sur la dissipation visqueuse en tout point, à l’exception de la sous-couche visqueuse à proximité des parois solides. Ici, le modèle de turbulence doit constamment réduire le niveau de turbulence, comme dans le cas des modèles bas Reynolds. Une alternative est d’utiliser de nouvelles conditions aux limites, calculées à l’aide de lois de parois.
Modèles bas Reynolds
Le terme “modèle bas Reynolds” semble contradictoire étant donné que les écoulements ne peuvent être turbulents que si le nombre de Reynolds est suffisamment grand. La notation “bas Reynolds” ne fait pas référence à l’écoulement à l’échelle globale, mais à la région en proche paroi dans laquelle les effets visqueux dominent; c’est à dire, la sous-couche visqueuse dans la figure ci-dessus. Un modèle bas Reynolds est un modèle qui reproduit correctement le comportement en limite de diverses variables de l’écoulement lorsque la distance à la paroi approche zéro. Un modèle bas Reynolds doit donc, par exemple, prédire que k~y2 lorsquey→0. Un comportement en limite correct signifie que le modèle de turbulence peut être utilisée dans l’ensemble de la couche limite, y compris dans la sous-couche visqueuse et dans la couche tampon.
La plupart des modèles utilisant ω sont des modèles bas Reynolds par construction. Mais le modèle standard k-ε et d’autres modèles k-ε communément rencontrés ne sont pas des modèles bas Reynolds. Certains d’entre eux peuvent, cependant, se voir ajouter des fonctions dites d’amortissement donnant le comportement correct en limite. Ils sont appelés modèles k-ε bas Reynolds.
Les modèles bas Reynolds donnent généralement une description très précise de la couche limite. Les gradients élevés en proche paroi requièrent cependant une résolution élevée du maillage, ce qui, par conséquent, signifie qu’une précision élevée est synonyme d’un coût numérique élevé. C’est la raison pour laquelle des méthodes alternatives pour la modélisation de l’écoulement proche paroi sont souvent utilisées pour des applications industrielles.
Lois de paroi
L’écoulement turbulent proche d’une paroi plane peut être divisée en quatre régions. A la paroi, la vitesse du fluide est nulle, et dans une fine couche au-dessus, la vitesse de l’écoulement évolue linéairement avec la distance à la paroi. Cette région est appelée sous-couche visqueuse, ou sous-couche laminaire. Plus loin de la paroi, une région est appelée la couche tampon. Dans cette zone tampon, les contraintes turbulentes commencent à dominer les contraintes visqueuses, et elle finit par être connectée à une région dans laquelle l’écoulement est complètement turbulent et la vitesse moyenne évolue avec le logarithme de la distance à la paroi. Cette zone est appelée région de loi logarithmique. Encore plus loin de la paroi, l’écoulement évolue vers la région d’écoulement libre. Les couches visqueuse et tampon sont très minces et si la distance à l’extrémité de la zone tampon est \delta, alors la région de loi logarithmique s’étendra jusqu’à une distance d’environ 100\delta de la paroi.
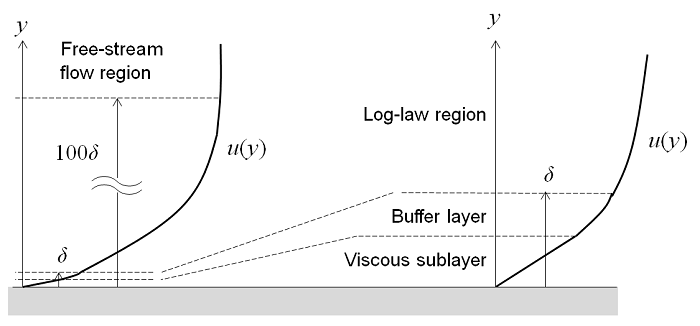
Il est cependant possible d’utiliser un modèle RANS pour calculer l’écoulement dans l’ensemble de ces quatre régions. Néanmoins, étant donné la faible épaisseur de la couche tampon, il peut être avantageux d’utiliser une approximation dans cette région. Les lois de paroi ne résolvent pas l’écoulement dans la couche tampon, et calculent de façon analytique une vitesse non nulle d’écoulement à la paroi. En utilisant une formulation en loi de paroi, vous utilisez une solution analytique pour l’écoulement dans la couche visqueuse et le modèle ainsi obtenu nécessitera moins de ressources de calcul. C’est une approche très utile pour beaucoup d’applications pratiques en ingénierie.
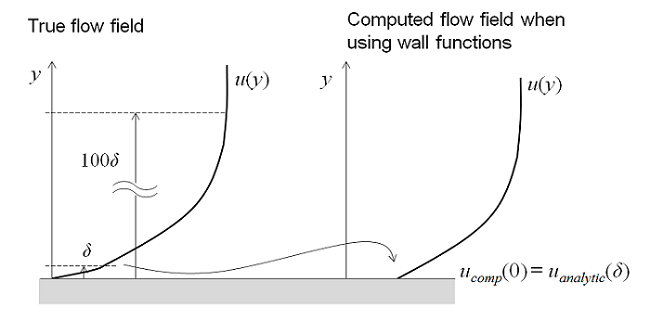
Si vous avez besoin d’un niveau de précision plus élevé que celui fourni par la formulation en loi de paroi, alors il sera préférable d’utiliser un modèle de turbulence qui résout l’ensemble du régime d’écoulement tel que décrit pour les modèles bas Reynolds ci-dessus. Par exemple, vous pourriez vouloir calculer la portance et la traînée d’un objet ou calculer le transfert de chaleur entre le fluide et la paroi.
Traitement automatique de la paroi
La fonctionnalité de traitement automatique de la paroi, une nouveauté de la version 5.3 de COMSOL Multiphysics®, combine les avantages des lois de parois et des modèles bas Reynolds. Le traitement automatique de la paroi adapte la formulation au maillage disponible dans le modèle, de façon à ce que vous obteniez à la fois robustesse et précision. Par exemple, pour un maillage de couche limite grossier, la fonctionnalité utilisera une formulation robuste en loi de paroi. Cependant, pour un maillage de couche limite dense, le traitement automatique de la paroi utilisera une formulation bas Reynolds afin de résoudre le profil de vitesse jusqu’à la paroi.
Le passage de la formulation bas Reynolds à la formulation loi de paroi se fait de façon progressive. Le logiciel mélange les deux formulations dans les éléments de frontière. Il calcule alors la distance à la paroi des points de grille des éléments de paroi (en unités visqueuses données par un décalage). La combinaison des formulations est alors utilisée dans les conditions aux limites.
Tous les modèles de turbulence présents dans COMSOL Multiphysics®, à l’exception du modèle k-ε, supportent le traitement automatique de la paroi. Cela signifie que les modèles bas Reynolds peuvent être utilisés pour des applications industrielles et que leur capacité de modélisation bas Reynolds est employée uniquement lorsque le maillage est suffisamment fin.
A propos des différents modèles de turbulence
Les huit modèles de turbulence RANS diffèrent par leur modélisation de l’écoulement en proche paroi, le nombre de variables additionnelles qu’ils résolvent, et ce que ces variables représentent. Tous ces modèles étendent les équations de Navier-Stokes avec un terme additionnel de viscosité turbulente, la différence portant sur la façon de calculer ce terme.
L-VEL et yPlus
Les modèles de turbulence L-VEL et yPlus algébrique calculent la viscosité turbulente à l’aide d’équations algébriques uniquement basées sur la vitesse locale du fluide et sur la distance à la paroi la plus proche. Ils ne résolvent aucune équation de transport supplémentaire. Ces modèles résolvent l’écoulement partout et sont les plus robustes et les moins coûteux en termes de ressources de calcul des huit modèles de turbulence. Bien qu’ils soient généralement les moins précis, ils fournissent de bonnes approximations pour les écoulements internes, en particulier dans les applications de refroidissement électronique.
Spalart-Allmaras
Le modèle Spalart-Allmaras ajoute une seule variable supplémentaire pour la viscosité cinématique turbulente non amortie. C’est un modèle bas Reynolds et il peut résoudre l’ensemble de l’écoulement jusqu’à la paroi solide. A l’origine, le modèle a été développé pour des applications aérodynamiques et a l’avantage d’être relativement robuste avec un coût de résolution modéré. L’expérience montre que ce modèle présente une précision moindre pour le calcul des champs d’écoulements de cisaillement, d’écoulements séparées ou d’écoulements à turbulence décroissante. Son avantage est qu’il est relativement stable et offre une bonne convergence.
k-ε
Le modèle k-ε résout deux variables: k, l’énergie cinétique turbulente, et ε (epsilon), le taux de dissipation de l’énergie cinétique turbulente. Des lois de paroi sont utilisées dans ce modèle, l’écoulement dans la couche tampon n’est donc pas simulé. Historiquement, le modèle k-ε est populaire pour des applications industrielles du fait de son bon taux de convergence et du fait qu’il requiert relativement peu de mémoire pour sa résolution. Il ne calcule pas très précisément les écoulements manifestant des gradients de pression adverses, une forte courbure, ou un jet. Il a une bonne performance pour des problèmes d’écoulements externes autour de géométries complexes. Le modèle k-ε peut par exemple être utilisé pour résoudre l’écoulement d’air autour d’un corps non profilé.
Les modèles de turbulence listés ci-dessous ont un caractère plus fortement non-linéaire que le modèle k-ε et peuvent souvent être difficiles à faire converger, à moins qu’une bonne estimation initiale soit fournie, cette dernière pouvant être obtenue à l’aide du modèle k-ε. Vous pouvez résoudre le modèle en utilisant le modèle k-ε puis utiliser la nouvelle fonctionnalité Générer une nouvelle interface de modèle de turbulence, disponible dans le module CFD dans la version 5.3 de COMSOL Multiphysics®.
k-ω
Le modèle k-ω est similaire au modèle k-ε, mais il résout ω (omega) — le taux de dissipation spécifique de l’énergie turbulente. C’est un modèle bas Reynolds, mais il peut également être utilisé avec des lois de paroi. Il est davantage non-linéaire, donc plus difficile à faire converger que le modèle k-ε, et est assez sensible à l’estimation initiale de la solution. Le modèle k-ω est utile dans de nombreux cas dans lesquels le modèle k-ε n’est pas précis, comme les écoulements internes, les écoulements avec de fortes courbures, les écoulements séparés et les jets. Un bon exemple d’écoulement interne est l’écoulement dans une conduite coudée.
k-ε bas Reynolds
Le modèle k-ε bas Reynolds est similaire au modèle k-ε mais ne nécessite pas de lois de paroi: il peut résoudre l’écoulement partout. C’est une extension logique du modèle k-ε et il partage nombre de ses avantages, mais requiert généralement un maillage plus dense; pas seulement au niveau des parois, mais partout où les propriétés de la formulation bas Reynolds interviennent et amortissent la turbulence. Il peut parfois être utile d’utiliser le modèle k-ε afin de calculer une bonne valeur initiale pour résoudre le modèle k-ε bas Reynolds. Une méthode alternative consiste à utiliser le traitement automatique de la paroi et commencer avec un maillage de couche limite grossier pour utiliser des lois de paroi, puis raffiner la couche limite au niveau des parois d’intérêt afin d’utiliser les modèles bas Reynolds.
Le modèle k-ε bas Reynolds peut calculer les forces de portance et de traînée ainsi que des flux de chaleur avec plus de précision que le modèle k-ε. Il a également montré une bonne prédiction de la séparation et du rattachement pour un certain nombre de cas.
SST
Le modèle SST combine le modèle k-ε dans la région d’écoulement libre et le modèle k-ω en proche paroi. C’est un modèle bas Reynolds et d’une certaine façon le modèle “à privilégier” pour des applications industrielles. En termes de ressources de calcul, il a les mêmes besoins que le modèle k-ω et le modèle k-ε bas Reynolds, mais sa formulation élimine certains défauts inhérents aux modèles purement k-ω et k-ε. Dans un modèle d’exemple, le modèle SST résout l’écoulement autour d’un Profil d’aile NACA 0012. Les résultats montrent une bonne cohérence avec les données expérimentales.
v2-f
Proche des parois, les variations de la vitesse sont généralement plus grandes dans les directions parallèles à la paroi que dans la direction perpendiculaire à la paroi. Les variations de vitesse sont dites anisotropes. Plus loin de la paroi, les variations ont une amplitude similaire dans toutes les directions. Les variations de vitesse deviennent isotropes.
Le modèle de turbulence v2-f décrit l’anisotropie de l’intensité de la turbulence dans la couche limite turbulente à l’aide de deux nouvelles équations, s’ajoutant aux deux équations de l’énergie cinétique turbulente (k) et du taux de dissipation (ε). La première équation décrit le transport des variations de la vitesse turbulente dans la direction normale aux lignes de courant. La seconde équation prend en compte les effets non locaux tels qu’un amortissement de la redistribution de l’énergie cinétique turbulente entre les directions normale et parallèles, induit par la paroi.
Vous devriez utiliser ce modèle pour des écoulements clos au-dessus de surfaces incurvées, par exemple, pour modéliser des cyclones.
Considérations sur le maillage pour les problèmes de CFD
Résoudre n’importe quel type d’écoulement fluide — laminaire ou turbulent — est coûteux en termes de ressources de calcul. Des maillages relativement fins sont requis et il y a de nombreuses variables à résoudre. Dans l’idéal, même si vous disposiez d’un ordinateur très rapide avec beaucoup de gigas de RAM pour résoudre ce type de problèmes, les simulations pourraient toujours prendre des heures ou des jours pour des modèles 3D plus gros. De fait, l’idée est d’utiliser le maillage le plus simple possible, tout en capturant l’ensemble des détails de l’écoulement.
Si l’on se réfère à l’illustration présentée en haut de ce billet de blog, on observe que pour une plaque plane (et pour la plupart des problèmes d’écoulement) le champ de vitesse varie assez doucement dans la direction tangente à la paroi, mais assez rapidement dans la direction normale, d’autant plus si l’on considère la couche tampon. Cette observation motive l’utilisation d’un maillage en couche limite. Ce type de maillage est proposé par défaut lorqu’on utilise le mailleur basé sur la physique, et insère de fins rectangles en 2D, ou des prismes triangulaires en 3D au niveau des parois. Ces éléments à fort rapport d’aspect permettent de bien résoudre les variations de la vitesse dans la direction normale à la paroi, tout en réduisant le nombre de point de calcul dans la direction tangente à la frontière.
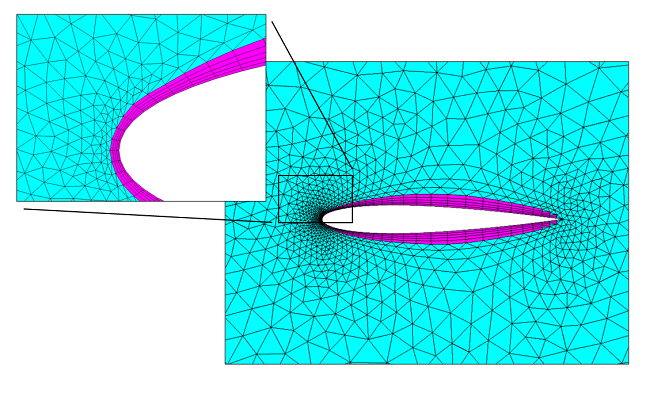
Le maillage en couche limite (magenta) autour d’un profil d’aile et le maillage triangulaire environnant (cyan) pour un maillage 2D.

Le maillage en couche limite (magenta) autour d’un corps non profilé et le maillage tétraédrique environnant (cyan) pour un maillage volumique 3D.
Evaluer les résultats de votre modèle de turbulence
Une fois que vous avez utilisé l’un de ces modèles de turbulence pour résoudre votre simulation d’écoulement, vous souhaiterez probablement vérifier que la solution est précise. Bien sûr, comme vous le feriez pour n’importe quel modèle d’éléments finis, vous pouvez simplement lancer votre simulation avec des maillages de plus en plus fins et observer comment la solution évolue lorsque le maillage est raffiné. Une fois que la solution ne varie pas dans un intervalle que vous trouvez acceptable, votre simulation peut être considérée comme ayant convergé par rapport au maillage. Il y a cependant des résultats additionnels que vous devez vérifier lorsque vous modélisez la turbulence.
Lorsque vous utilisez des formulations avec loi de paroi, il est nécessaire de vérifier la résolution à la paroi en unités visqueuses (ce graphique est généré par défaut). Cette valeur vous indique à quelle distance de la couche limite commence votre domaine de calcul, et ne devrait pas être trop grande. Dans le cas où la résolution à la paroi dépasse quelques centaines, vous devriez songer à raffiner le maillage dans la direction normale aux parois. La seconde variable qu’il est important de vérifier lorsque vous utilisez des lois de paroi est le décalage de paroi (en unité de longueur). Cette variable est associée à l’épaisseur supposée de la couche visqueuse et devrait être petite par rapport aux dimensions environnantes de la géométrie. Si ce n’est pas le cas, vous devriez également raffiner le maillage dans ces régions.
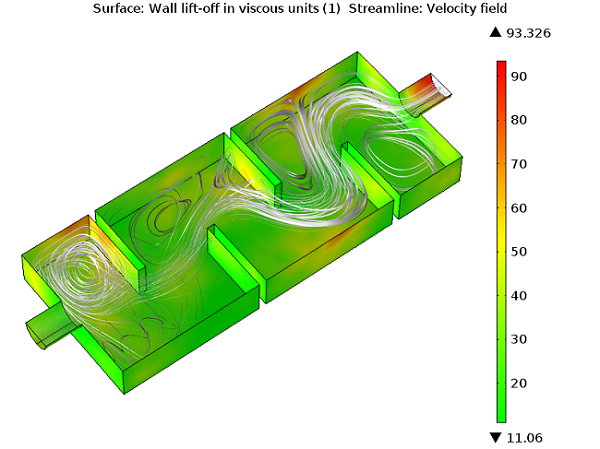
Le décalage de paroi maximal en unités visqueuses est inférieur à 100, il n’y a donc pas besoin de raffiner le maillage de couche limite.
Lorsque vous simulez un écoulement en utilisant un traitement bas Reynolds, vérifiez la distance adimensionnée au centre de la cellule (le graphique est généré par défaut). Cette valeur devrait être de l’ordre de l’unité partout pour les modèles algébriques, et inférieure à 0.5 pour tous les modèles à deux équations ainsi que le modèle v2-f. Si ce n’est pas le cas, raffinez le maillage dans ces zones.
Pour conclure
Dans ce blog, nous avons discuté des différents modèles de turbulence disponibles dans COMSOL Multiphysics®, en mettant l’accent sur quand et pourquoi vous devriez utiliser chacun d’entre eux. Le logiciel COMSOL® montre sa vraie plus-value lorsque vous voulez combiner votre simulation d’écoulement avec d’autres phénomènes, par exemple trouver les contraintes exercées par des vents violents sur un panneau solaire, modéliser la convection forcée dans un échangeur de chaleur, ou le transfert de masse dans un mélangeur, entre autres.
Si vous êtes intéressé pour utiliser le logiciel COMSOL® pour vos simulations CFD et multiphysiques, ou si vous avez une question qui n’est pas adressée ici, vous pouvez nous contacter.



Commentaires (0)