You can use the residual operator, new with COMSOL Multiphysics® version 5.2, to evaluate and plot your model’s algebraic residual in order to troubleshoot convergence issues. This blog post demonstrates the use of the residual operator for visualizing and understanding the convergence properties of a turbulent flow simulation.
What Is the Algebraic Residual?
When solving a finite element model, it is important to know how accurate the results are. Depending on the mesh (the discretization) and the nature of the equations for which you solve, the algebraic residual is only one of several error sources. The following sources contribute to the computation error:
- The truncation error (also called the Galerkin error for the finite element method).
- The quadrature error made by using numerical methods to approximate the finite element integrals.
- The geometrical approximation error made by representing the actual geometry by a polynomial representation, which is a sort of integration error for elements adjacent to or on a curved boundary.
- The algebraic error obtained by terminating the solvers prematurely (or by using a sloppy tolerance). This is the error that you can access using the residual operator.
Normally, the algebraic error is (and should be) much smaller than the truncation error. However, if you run into convergence issues, the algebraic residual is not small and can reveal where the cause of the issue resides in your model.
Contrary to the related information that COMSOL Multiphysics® already provides, such as convergence numbers, which are scaled global numbers, the residual operator provides an unscaled residual value for each variable in a model. It also shows a spatial distribution of the residual for that quantity. The residual is the latest-computed residual vector from the finite element discretization, but interpreted as a continuous spatial field quantity. The spatial distribution helps you pinpoint where in the modeling domain the residual is relatively large and therefore will hamper convergence of the solution. Possible problems in the model could be:
- Insufficient mesh resolution in that part of the modeling domain
- Sharp corners in the geometry
- Inappropriate or incompatible boundary conditions
Let’s see exactly how to plot and evaluate the algebraic residual in your model with the residual operator.
How to Add the Algebraic Residual to a Model
The residual operator is available for stationary and time-dependent simulations. To add the residual operator to the model, you need to activate it using a setting in the Advanced subnode to a stationary or time-dependent solver. By default, the Store latest residual setting is Off. To compute the residual, choose While solving, or to compute it and store it in the output for postprocessing, choose While solving and in output. Storing the residual in the output so that you can use it in plots and for general postprocessing requires additional memory resources, but this is not necessary if you want to plot the residual while solving only.
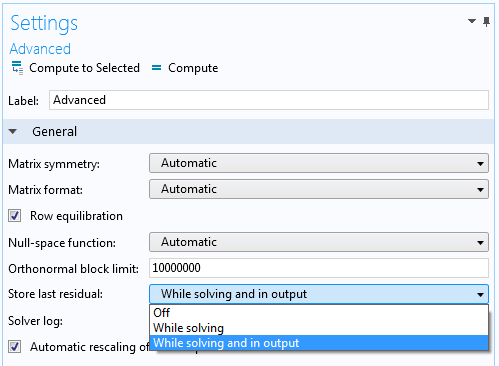
Settings for specifying the storage of the last residual values.
Using the Residual Operator in COMSOL Multiphysics®: A Fluid Dynamics Example
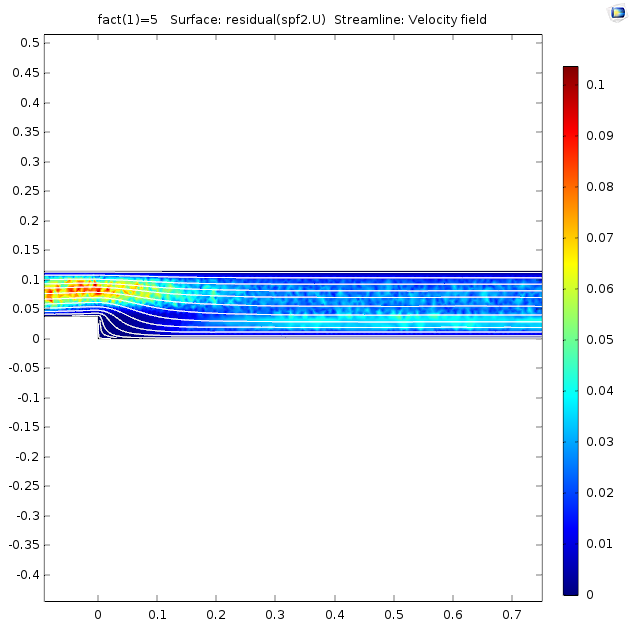
To demonstrate how the residual operator can provide insight into how numerical disturbances can enter and propagate in a finite element model, consider the Turbulent Flow Over a Backward Facing Step example model from the Application Gallery. This example uses the k-ɛ turbulence model. The model features a classic 2D geometry of a backward facing step with a corner that causes a recirculation zone in a turbulent fluid flow simulation.
This version of the model includes plotting the residual in the momentum equations (the velocity field) while solving. To do so, a Velocity plot group contains a Surface plot node with the expression residual(spf2.U), where spf2.U is the velocity magnitude.
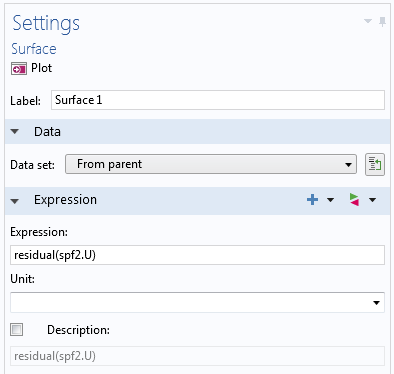
The Segregated solver settings with the plot of the residual, specified under Results While Solving.
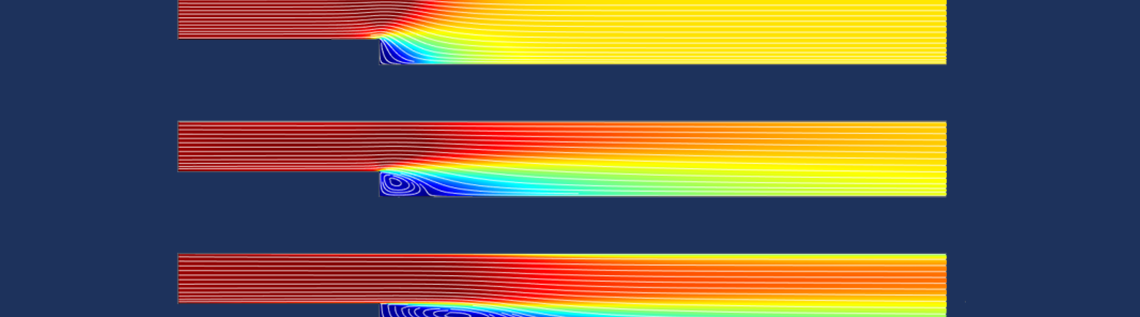
This example is a nice illustration of what happens when you solve transport problems with some sort of stationary approach — in this case, pseudo time stepping. The residual caused by the “backstep disturbance” needs to be transported out of the region. The residual does not drop until the “disturbances” have been transported out of the channel and the simulation can finish. The screenshots below show how the area where the residual is relatively large moves from the inlet area toward the outlet.
The residual for the velocity field at the beginning and toward the end of the solution.
The convergence plot confirms that the initially sluggish convergence changes to a quick convergence in just a few iterations once the large residual has disappeared. This behavior is consistent with the fact that perturbations and errors evolve according to the approximated equation — in this case, an approximation of time-dependent, convection-dominated flow equations. The errors therefore need time, which corresponds to iterations for pseudo time stepping, to be transported out of the domain.
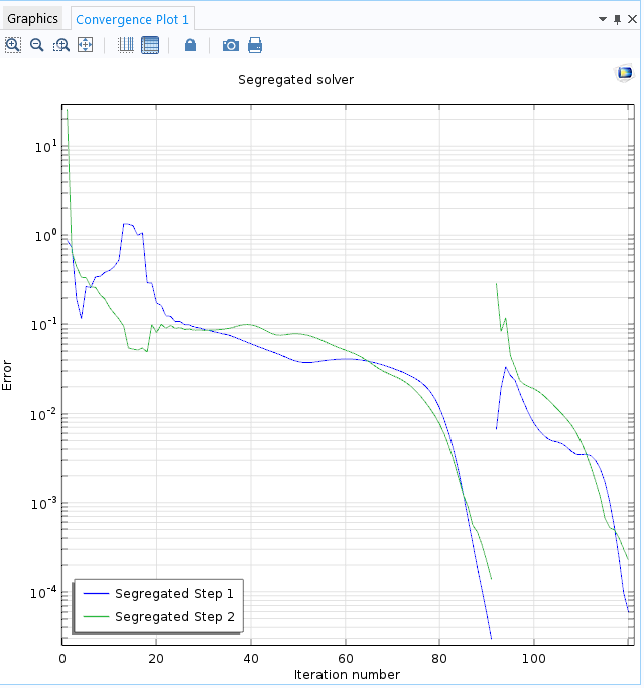
The convergence plot for the Turbulent Flow Over a Backward Facing Step tutorial model. Notice the fast convergence toward the end.
By plotting and evaluating the algebraic residual, you can troubleshoot models that do not converge or converge slowly, so that you can find your simulation results as quickly and efficiently as possible.
Some Aspects to Consider When Using the Residual Operator
There are a couple of cases where you need to consider how to apply the residual operator:
The algebraic residual data only makes sense for actual time steps taken by the solver. For interpolated output, which is the default, the COMSOL Multiphysics® software does not store any values for the residual; you therefore get an empty plot for the interpolated times. There are two ways in which you can study the residual for time-dependent problems (assuming you have set Store last residual to While solving and in output):
- Change the Update at setting for the plot, while solving, to Times steps taken by solver, and select a plot that is using the residual operator.
- Change the Times to store setting for the Time-Dependent Solver node, under the Output section, to Steps taken by solver. This approach also makes the residual available for results evaluation.
Also, a single constrained degree of freedom (DOF) will, by definition, have a residual that is zero. If, however, several DOFs are involved in a constraint, the residual will be returned as zero for all of them. For example, if the constraint, u + v = 0, is added, then, \text{residual(u)} = \text{residual(v)} = 0, on the selection where that constraint is, is active. There are many built-in constraints that have this property (for example, roller conditions in solid mechanics where \textbf{u} \times \textbf{n} = 0).
This aspect applies to pointwise constraints; weak constraints do not have this property (that constrained DOFs are set to zero).
Further Resources
- Read this blog post to learn how to use viscosity ramping, another method to improve convergence for your CFD models
- Browse the COMSOL Blog for additional posts on how to make full use of the solving capabilities of COMSOL Multiphysics®
Editor’s note: This blog post was updated on February 29, 2024, to include mention of some aspects to consider when using the residual operator.






Comments (8)
Michael Rembe
August 19, 2016Hello Magnus,
thank you very much for your explanations. The residual helps to evaluate the solution and to get an idea about convergence problems.
If you miss the residual, COMSOL52a doesn’t save any residuals in the case you cancel simulation by a stop condition (with saving results). In this case you get the residual by results during simulation.
Best regards
Ulrik Thisted
September 20, 2016Hello,
This feature sound very useful and I have missed it in the past.
Best regards
Ulrik
Milan Patel
December 1, 2016Me too! This would be great.
Daniele
September 28, 2020Hello,
thank you for this post, I found it useful. However, I’m still not able to plot my residuals: when I try to follow your instructions, I just get a blank graph of my domain.
Do you know if the “residual” operator has any incompatibility with my Comsol version (5.4)?
Also, I would like to ask another thing: besides the standard convergence plot, which is shown by Comsol during the calculations, is it possible to plot the scaled residuals of each dependent variable, while the solver is running? The only way I know to do such a thing is to define a probe, which I can monitor during the calculations, but I don’t know how to invoke the residuals within the “Expression” text box.
Thank you so much for any help.
Kind regards
Daniele
Magnus Ringh
September 29, 2020 COMSOL EmployeeHello Daniele,
This sounds strange. Please contact our technical support team for assistance.
Best regards,
Magnus Ringh, COMSOL
Mojmir Michalek
February 14, 2024I have the same problem as Daniele. Blank graph of my domain appears when using residual operator. Storing is set to “While solving and in output”. I use modal solver in this particular case, if this helps. This functionality would save me hours or even days!
Magnus Ringh
February 14, 2024 COMSOL EmployeeHi Mojmir,
Again, this sounds strange. Please contact our technical support team for assistance.
Best regards,
Magnus
Magnus Ringh
February 15, 2024 COMSOL EmployeeHi again,
Regarding a zero or empty residual, there might be one of these conditions:
1. The algebraic residual data only makes sense for actual time steps taken by the solver. For interpolated output, which is the default, the COMSOL Multiphysics software does not store any values for the residual; you therefore get an empty plot for the interpolated times. To fix this, use the time steps from the solver.
2. A single constrained DOF will, by definition, have zero residual. If, however, several DOFs are involved in a constraint, the residual will returned as zero for all of them. As an example, if the constraint u+v=0 is added, then residual(u) = residual(v) = 0 on the selection where that constraint is active. There are many built-in constraints that have this property (for example, roller conditions in solid mechanics).