La Bibliothèque d'Applications présente des modèles construits avec COMSOL Multiphysics pour la simulation d'une grande variété d'applications, dans les domaines de l'électromagnétisme, de la mécanique des solides, de la mécanique des fluides et de la chimie. Vous pouvez télécharger ces modèles résolus avec leur documentation détaillée, comprenant les instructions de construction pas-à-pas, et vous en servir comme point de départ de votre travail de simulation. Utilisez l'outil de recherche rapide pour trouver les modèles et applications correspondant à votre domaine d'intérêt. Notez que de nombreux exemples présentés ici sont également accessibles via la Bibliothèques d'Applications intégrée au logiciel COMSOL Multiphysics® et disponible à partir du menu Fichier.
Silicon carbide (SiC) epitaxial furnaces are a specialized equipment for the production and preparation of SiC epitaxial wafers. This example model demonstrates the process of preparing an SiC epitaxial wafer based on the physical vapor transport (PVT) method in a furnace. This involves ... En savoir plus
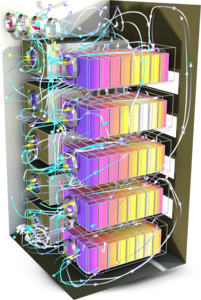
High-power battery energy storage systems (BESS) are often equipped with liquid-cooling systems to remove the heat generated by the batteries during operation. This tutorial demonstrates how to define and solve a high-fidelity model of a liquid-cooled BESS pack which consists of 8 ... En savoir plus
This model describes the three heat transfer modes: conduction, convection, and radiation, combined with nonisothermal flow in a realistic geometry representing a light bulb and the surrounding air. The LED chips dissipate heat. The model computes the equilibrium temperature induced by ... En savoir plus
During the design of a building, environmental issues have gained considerable influence in the entire project. One of the first concerns is to improve thermal performances. In this process, simulation software are key tools to model thermal losses and performances in the building. The ... En savoir plus
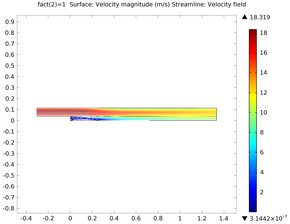
The backward facing step is an interesting case for studying the performance and solution strategy of a turbulence model. In this case, the flow is subjected to a sudden increase of cross-sectional area, resulting in a separation of flow starting at the point of expansion. Spatial ... En savoir plus
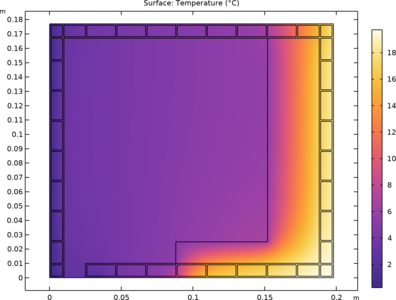
This model how to build and solve a conductive heat transfer problem using the Heat Transfer interface. The model, taken from a NAFEMS benchmark collection, shows an axisymmetric steady-state thermal analysis. As opposed to the NAFEMS benchmark model, we use the temperature unit kelvin ... En savoir plus
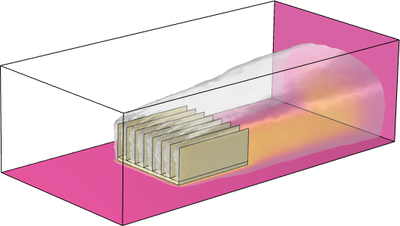
Tutorial model of an air-cooled battery energy storage system (BESS). The model includes conjugate heat transfer with turbulent flow, fan curves, internal screens, and grilles. It features several interesting aspects: Fully parameterized geometry, which can be modified for different ... En savoir plus
Thermoelectric elements are often used to cool or heat electronic components to a desired temperature. In such simulations, you are typically not interested in the behavior of the thermoelectric element itself but want to use its performance characteristics to model the overall response ... En savoir plus
This app demonstrates the following: A model using symmetry while the results are visualized in full 3D Provides info if the results are above or below certain critical values Selecting predefined or user-defined materials Error control of geometry parameters using methods and ... En savoir plus
The drive for miniaturizing electronic devices has resulted in today’s extensive use of surface-mount electronic components. An important aspect in electronics design and the choice of materials is a product’s durability and lifetime. For surface-mount resistors and other components ... En savoir plus