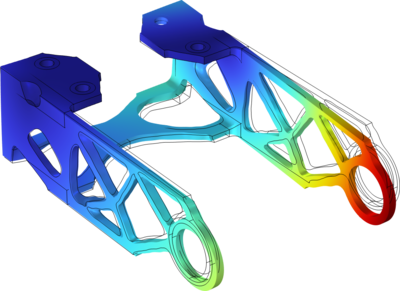La Bibliothèque d'Applications présente des modèles construits avec COMSOL Multiphysics pour la simulation d'une grande variété d'applications, dans les domaines de l'électromagnétisme, de la mécanique des solides, de la mécanique des fluides et de la chimie. Vous pouvez télécharger ces modèles résolus avec leur documentation détaillée, comprenant les instructions de construction pas-à-pas, et vous en servir comme point de départ de votre travail de simulation. Utilisez l'outil de recherche rapide pour trouver les modèles et applications correspondant à votre domaine d'intérêt. Notez que de nombreux exemples présentés ici sont également accessibles via la Bibliothèques d'Applications intégrée au logiciel COMSOL Multiphysics® et disponible à partir du menu Fichier.
This app demonstrates the following: Playing a sound at a specific computed frequency Selecting different materials from a combo box Visualizing material appearance, color, and texture Choice of three different user interface layouts for computer, tablet, or smartphone Custom ... En savoir plus
This example shows how to perform a topology optimization with several load and constraint cases. The density feature for topology optimization is used together with a parametric sweep where each optimized solution is used as input for a further improved optimization. The final ... En savoir plus
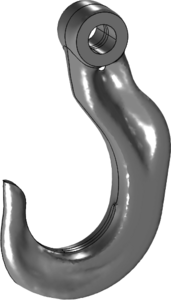
The model studies optimal material distribution in a hook, which is symmetric about the z plane and consists of a linear elastic material, structural steel. It is subjected to two distributed edge load cases: One at the tip of the hook and one along its lower inner curve. The geometry is ... En savoir plus
The topology optimized Tesla microvalve is used as an inspiration for an initial geometry. Second order Bernstein polynomials are used to perturb the shape of the geometry. The resulting design is remeshed in the deformed configuration and the performance is investigated for a range of ... En savoir plus
This model presents two examples of topology optimization of the magnetic circuit of a loudspeaker driver. A first optimization is used to find the design of a nonlinear iron pole piece and top plate that maximize the BL factor at the resting position (small displacements), while ... En savoir plus
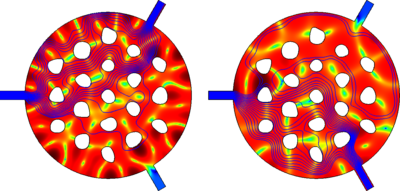
This model shows how shape optimization can be used to design an acoustic demultiplexer. A demultiplexer is a data distributing device, in this case it will distribute acoustic energy. The geometry consists of a circular domain with one input port and two output ports. The domain has the ... En savoir plus
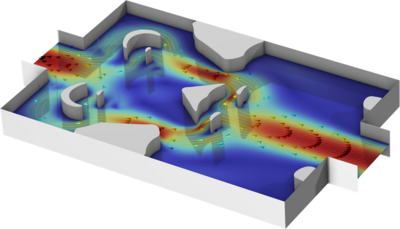
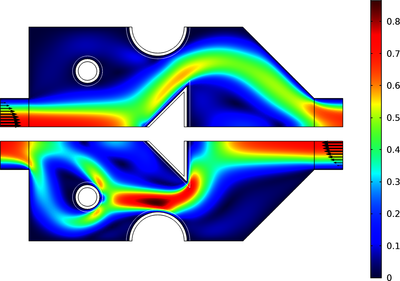
This model performs a topological optimization for a Tesla microvalve. A Tesla microvalve inhibits backwards flow using friction forces rather than moving parts. The design can be optimized by distributing a specific amount of material within the modeling domain. The goal is to maximize ... En savoir plus
The topology optimized Tesla microvalve is used as inspiration for a parametrized geometry. The optimization of this geometry takes erosion and dilation of the geometry into account by optimizing over a parametric sweep. In this example the optimization is driven by the worst of the 3 ... En savoir plus
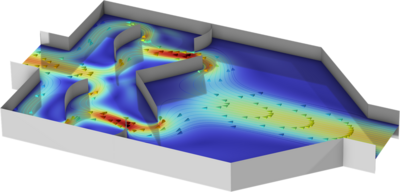
The mass of an aluminum beam is minimized subject to a displacement constraint and a distributed load. The problem is solved using parameter, shape and topology optimization. En savoir plus
A demonstration of topology optimization using the Structural Mechanics Module and the Optimization Module. The classical MBB beam is solved in 2D using a Helmholtz filter and Solid Isotropic Material Penalization (SIMP) technique to recast the original combinatorial optimization problem ... En savoir plus