
Creating new physics interfaces that you can save and share, modifying the underlying equations of a model, and simulating a wider variety of devices and processes: These are just a few ways you can benefit from the equation-based modeling capabilities of the COMSOL Multiphysics® software.
Using Equation-Based Modeling in Your Simulations
With equation-based modeling, part of the core functionality of COMSOL Multiphysics, you can create your own model definitions based on mathematical equations and directly input them into the software’s graphical user interface (GUI).
These abilities give you complete control over your model, so you can tailor it to your exact specifications and add complexity as needed. To provide this flexibility, COMSOL Multiphysics uses a built-in interpreter that interprets equations, expressions, and other mathematical descriptions before producing a model. In addition, you can use tools like the Physics Builder to create your own physics interfaces, or the Application Builder to create entire new user interfaces.
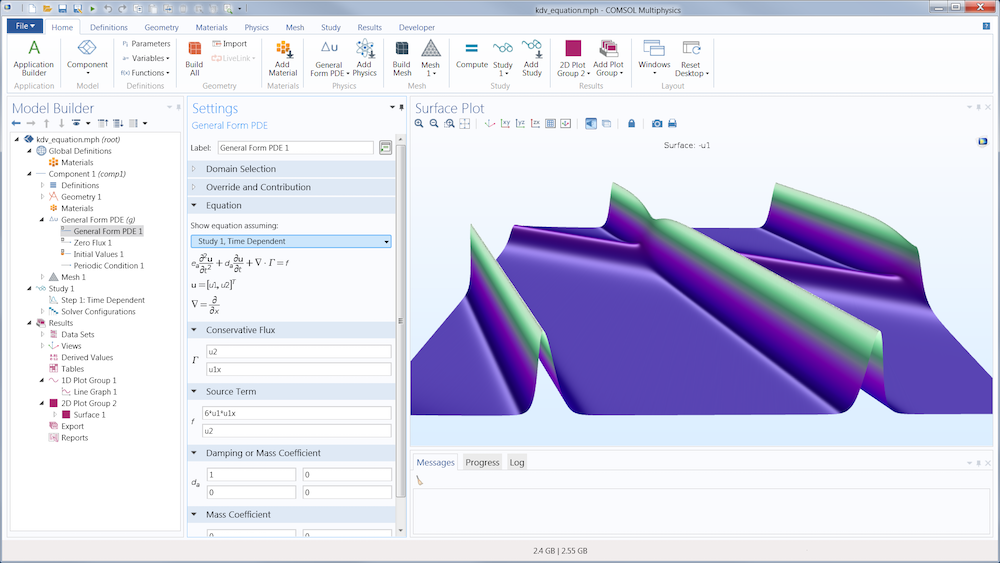
Example of entering a custom partial differential equation into the COMSOL Multiphysics GUI.
Using this functionality, you can work with:
- Partial differential equations (PDEs)
- Ordinary differential equations (ODEs)
- Algebraic equations
- Differential algebraic equations (DAEs)
- Arbitrary Lagrangian-Eulerian (ALE) methods
- Curvilinear coordinate computation
- Sensitivity analysis
There is no limit to how creative you can be when setting up and solving your models with equation-based modeling, which expands what you can achieve with simulation. To show this functionality in action, let’s take a look at three examples…
Example 1: The KdV Equations and Solitons
In 1895, the Korteweg-de Vries (KdV) equation was created as a means to model water waves. Since the equation doesn’t introduce dissipation, the waves travel seemingly forever. These waves are now called solitons, which are seen as single “humps” that can travel over long distances without altering their shape or speed.
Today, engineers use the KdV equation to understand light waves. As a result, one of the main modern applications of solitons is in optical fibers.
Simulating the KdV Equations with Equation-Based Modeling
To solve the KdV equation in COMSOL Multiphysics, users can add PDEs and ODEs into the software interface via mathematical expressions and coefficient matching. It’s also possible to easily define dependent variables and identify coefficients via the General Form PDE interface.
With this setup, users are able to model an initial pulse in an optical fiber and the resulting waves or solitons. According to the KdV equation, the speed of the pulse should determine both its amplitude and width, which can be observed via simulation. In addition, the simulation reveals that, just like with linear waves, solitons can collide and reappear while maintaining their shape. This counterintuitive finding would be challenging to observe without simulation.
If you want to learn more about this example, see the KdV equation model in the Application Gallery.
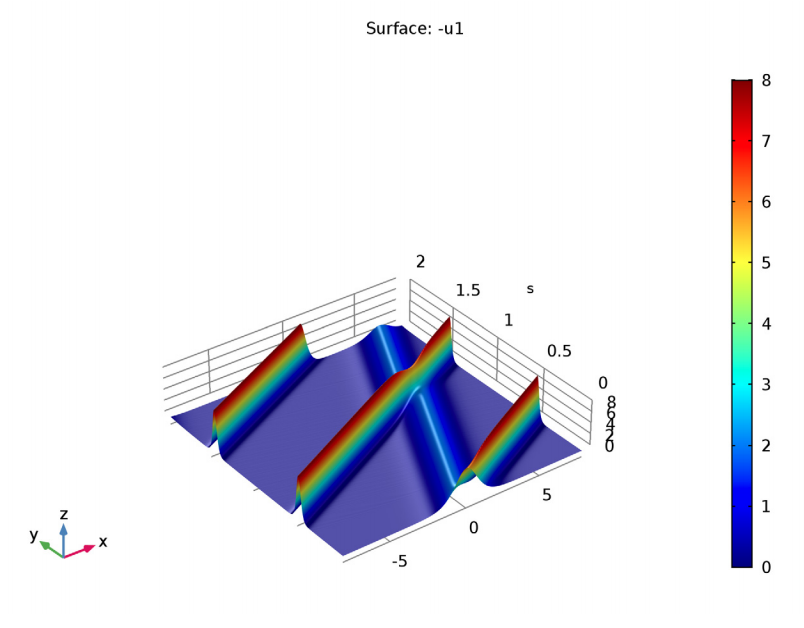
Simulation showing how solitons maintain an intact shape when colliding and reappearing.
Example 2: Electrical Signals in a Heart
Moving on to a medical example, let’s see how simulation can be used to understand the rhythmic patterns of contractions and dilations in a heart. The rhythmic contractions are triggered when the heart passes an ionic current through the muscle. During this process, ions flow through small pores that exist in an excitation (open) or rest (closed) state within the cellular membrane. As such, to gain a better understanding of heart patterns, the electrical activity in cardiac tissue needs to be examined.
Studying the electrical signals in a heart is not a simple process and involves modeling excitable media. To address this challenge, users can implement two sets of equations to describe various aspects of the electrical signal propagation. One such example is the Electrical Signals in a Heart model, provided through the courtesy of Dr. Christian Cherubini and Prof. Simonetta Filippi from the Campus Bio-Medico University of Rome in Italy. The equations used in this model, FitzHugh-Nagumo and complex Ginzburg-Landau, are included in the PDE interfaces available in COMSOL Multiphysics.
Using 2 Different PDEs to Analyze Electrical Signal Propagation in Cardiac Tissue
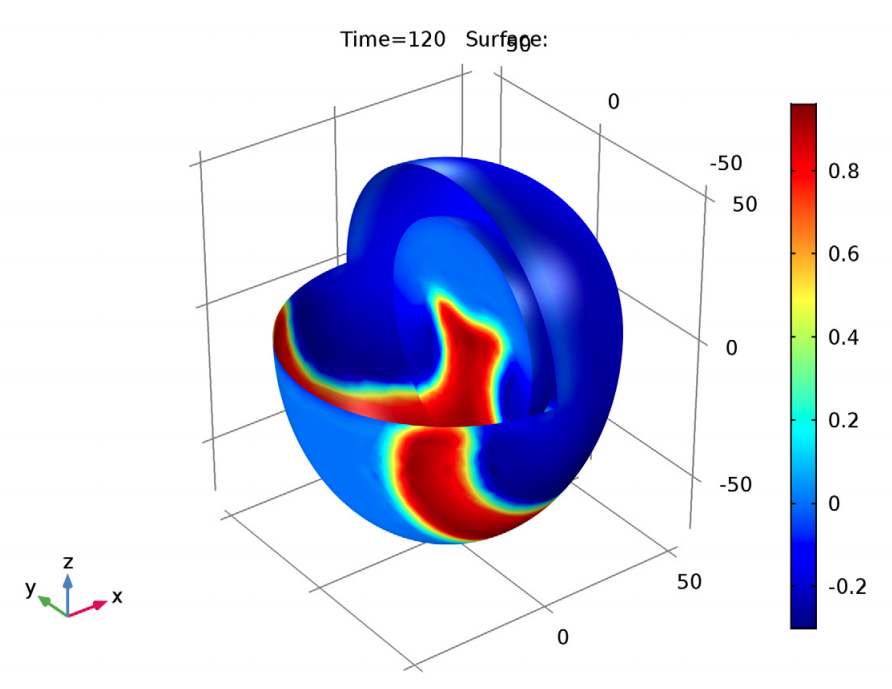
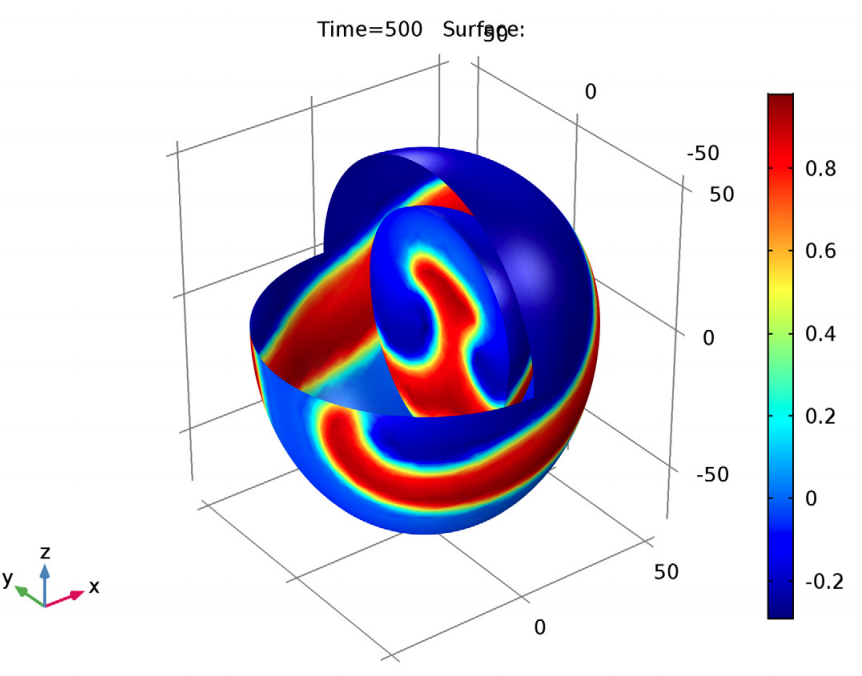
By using the FitzHugh-Nagumo equations to simulate excitable media, it is possible to create a simple physiological heart model with two variables: an activator (corresponding to the electric potential) and inhibitor (the voltage-dependent probability that the membrane’s pores are open and can transmit ionic current). Using these equations and various parameters, users can visualize a reentrant wave that moves around the tissue without damping, which results in a characteristic spiral pattern. In the context of electrical signals, this pattern could generate effects similar to those of arrhythmia, a condition that disturbs the normal pulse of a heart.
Solving the FitzHugh-Nagumo equations at times of 120 (left) and 500 (right) seconds.
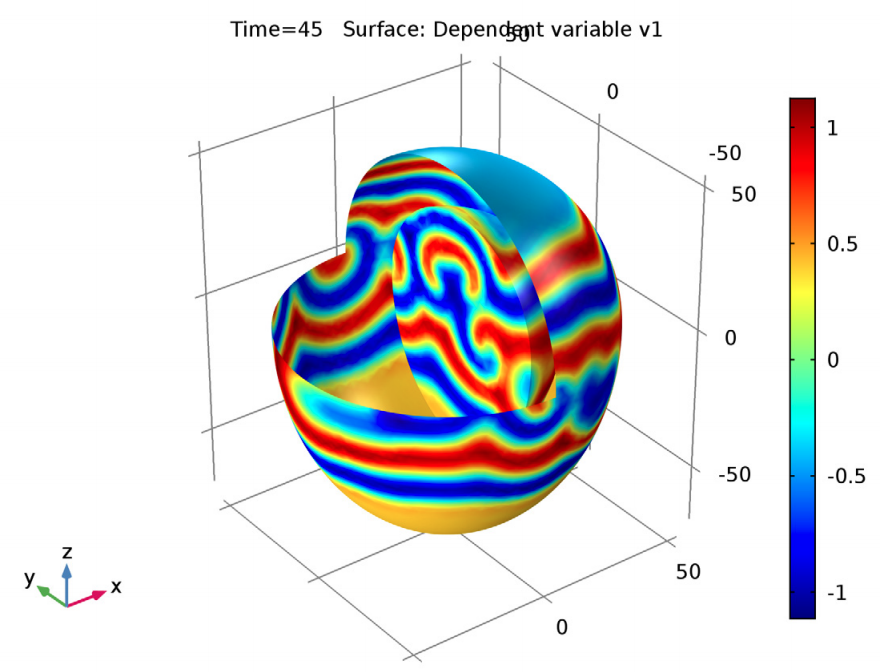
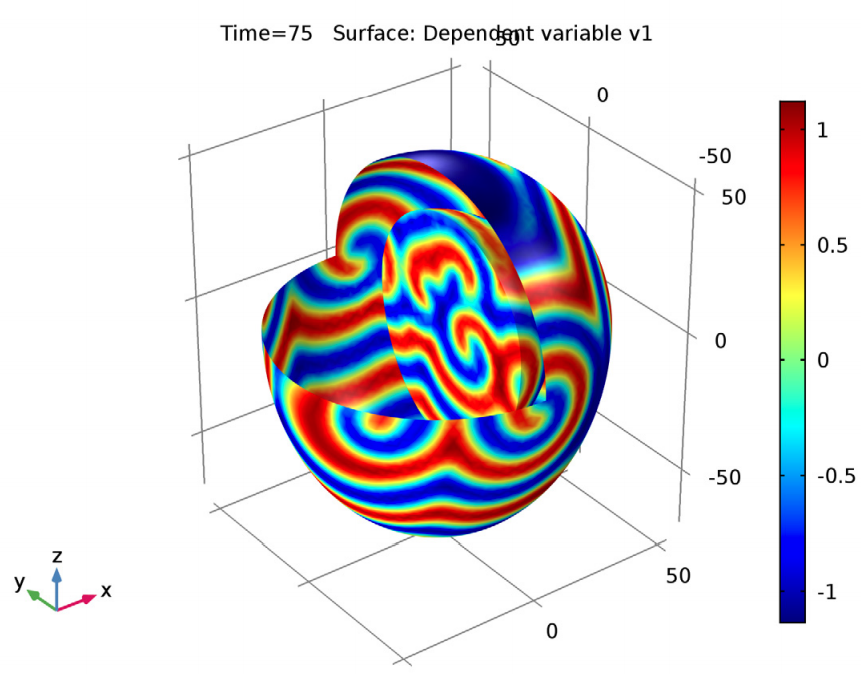
The complex Ginzburg-Landau equations help to model some parts of the transition from periodic oscillatory behavior to a chaotic state. During this transition, the amplitude of oscillations gradually increases and the periodicity decreases. These equations are used to study the dynamics of spiral waves in excitable media. The results show the diffusing species and the characteristic spiral patterns, which increase in complexity over time.
Solving the complex Ginzburg-Landau equations at times of 45 (left) and 75 (right) seconds.
Using both sets of equations enables the visualization of complicated real-world phenomena.
Example 3: A Lorenz Attractor
Lastly, let’s take a look at the Lorenz equations, which were developed to serve as a simple mathematical model for atmospheric convection. When using certain parameter values and initial conditions, a system of ODEs (a Lorenz system) has chaotic solutions. One such solution is a Lorenz attractor, which looks like a figure eight or butterfly when plotted in the phase space.
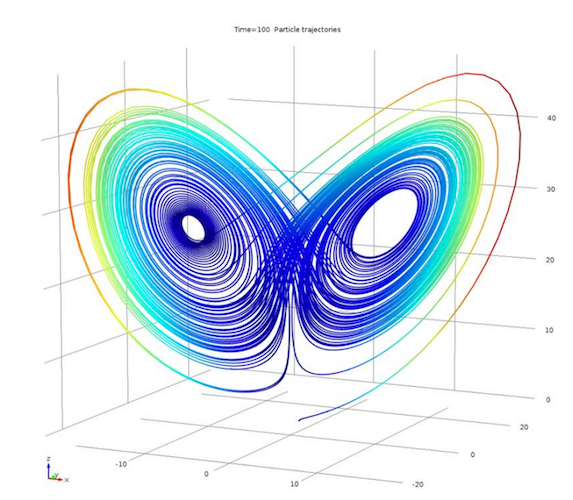
Example of the typical shape of a Lorenz attractor.
Using ODEs to Model a Lorenz Attractor
To solve the Lorenz attractor model, the Lorenz equations — a system of three coupled ODEs that contain three degrees of freedom — need to be added into the software. This is a straightforward process when using the Global ODEs and DAEs interface to define the Lorenz system.
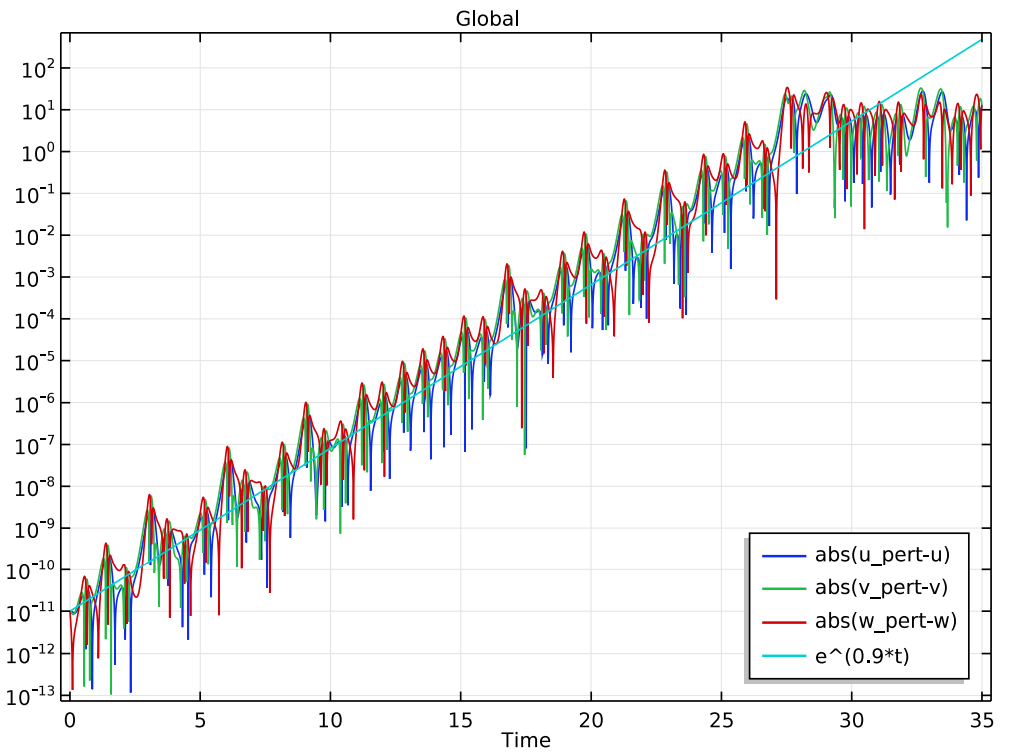
Next, users can view an initial solution close to the attractor and study the growth of a very small perturbation to this initial data. The results (seen in the left image below) visualize how the difference between the original and perturbed problems increases over time. In addition, the simulation demonstrates that with the chosen parameter values, the Lorenz system behaves like a Lorenz attractor, with results showing the butterfly shape that these attractors are known for.
The differences between the unperturbed and perturbed solutions over time (left) and the normal pattern for a Lorenz attractor (right).
Next Step
Watch a quick video introduction to COMSOL Multiphysics to learn more about the software’s key features. When you’re ready, request a software demonstration.







Comments (4)
Kaleem Iqbal
September 28, 2018Hi
I am new COMSOL, but I understand few things. My focus is to solve nonNewtonian problem with addition of temperature effect or energy. So, how I develop my new PDE or physical problem. Thanks in advance
Athena Serra
February 22, 2019How to write the average Nusselt formulation: -8*Al*Al*integral of(-dT/dz(r,0)*r*dr)from(0 to 1/2/Al). Thanks. My Email: athenaserra@gmail.com
Williams Baah
April 30, 2019Hi , any idea on how I can get the properties for Potassium Sodium Niobate for simulation in COMSOL?
Armin Abbasalinejad
February 20, 2020I have made a solid-state battery model based on electrochemical PDEs in COMSOL. Here is the link to my model: https://www.researchgate.net/publication/334724548_model2mph?_sg=7xnb1zSpi-CINUAzRvo9VdZOMFw2LyRFF1ktU5yvmAtDLpKkaCfw0Nl2Yz64ZTgmezryctFLRcN1fwltzszT3gm9vx3WzwbUBae8iH6n.5e0t9FTZ4WEVDBfFVIMOtaFm4Fek_p4nV7DJH-_J0Kx-psc68rt2whxg2VqhVSVfbwUeAvzY0jNABl3Ek13hgQ