
When watching your favorite creature feature, have you ever wondered what would happen if giant monsters actually roamed the Earth? To find out how we could best protect ourselves, a pair of mathematical biologists from Cardiff University and the University of Oxford used mathematical modeling to test common strategies used in films for eradicating these massive threats. By analyzing the simulations, they further determined which strategies work best for different regions.
Applying Real-Life Ecology Problems to Monster Eradication
A group of scientists exploring the deep recesses of the Mariana Trench accidentally free a giant prehistoric shark, a Megaladon, via a break in the thermocline. Subsequently, they blow through much of their available weaponry, technology, and crew (not to mention movie runtime) hunting The Meg. In a similar whale of a tale, a supersized great white shark terrorizes a fictional resort island with its Jaws…until the protagonist sends it back (in pieces) to the watery depths from whence it came.
Jaws was filmed on Martha’s Vineyard, Massachusetts, off the coast of Cape Cod, where in the real world, the shark population has been rapidly propagating in recent years. While shark attacks on humans are much, much rarer than the film would have you believe, the surge in dorsal fins spotted by beachgoers is worrying visitors and residents alike. What, exactly, is bringing a surplus of great whites so close to shore?

A great white shark. Image by Olga Ernst — Own work. Licensed under CC BY-SA 4.0, via Wikimedia Commons.
The short answer is the sharks’ food supply: seals. The long answer is a little more complicated: From the 1880s to the 1960s, New England fishermen saw seals as a threat to the fishing industry because the seals were picking off cod. People hunted the seals in great numbers until the seal population diminished from the area. Then, in the 1970s, the Marine Mammal Protection Act made it illegal to kill marine mammals, so the seal population returned…and so have the sharks.
Some people are ready to cull the seals, others want to cull the sharks, and suggested culling methods for either species could make the problem worse (though none involve the cinematic action deployed in summer blockbusters). So, how can we predict which options will have the desired outcomes and which might have unintended consequences? One way is by applying mathematics to biology…
Theoretical Population Ecology
In an attempt to spark interest in real-life ecology problems (like the great white’s return to the Cape), mathematical biologists Dr. Thomas Woolley and Prof. Philip Maini turned to thrilling creature features. They applied theoretical population ecology mathematics to a fictional scenario focusing on giant monsters known as Kaijus and giant robots known as Jaegers, based heavily on “evidence” found in movies representative of the genre, such as Pacific Rim, Jurassic World, and various Godzilla and King Kong flicks. This canonical evidence guided them through determining parameters for their simulations, as we will see later on.
Although the massive scale and suspension of disbelief needed for this scenario make it fun to explore, the basics revolve around what is already found in nature: species dynamics. For Woolley, using movie analogies to draw attention to population ecology was a question of “How do we show math in its best light?” He points out that one could just as easily compare a zombie apocalypse to the spread of malaria or the flu — the mathematical modeling is the same. For the monster situation, the biologists looked at real-life examples of competition between species, predator-prey interactions, and ad hoc eradication attempts by humans.
Ecology pest problems can be investigated mathematically using common tools like the predator-prey equations, which are built into the COMSOL Multiphysics® software. Officially called the Lotka–Volterra equations, these equations mathematically describe the way two species interact with one as the predator and the other the prey, as well has how their populations change over time. Using the predator-prey interaction problem as a basis for the Kaiju scenario, the researchers began their calculations…
Mathematical Modeling of the Kaiju Population
Before getting into eradication strategies, the biologists defined parameters for the Kaijus to predict the population size based on the following main criteria:
- Interactions
- Movement
- Environmental boundaries
- Initial distribution
Kaiju canon indicates that not only are these creatures able to reproduce but also that they fight each other when their population is too large and they must compete for resources. Therefore, the scientists used a logistic growth differential equation for the interaction part of the model. In real life, this type of equation is used for populations ranging from yeast to wolves.
For movement, the scientists determined that the beasts would be able to go from ocean to land in less than a day, based on such abilities in the popular films about them, and calculated how fast they move based on the 24-hour time period it takes to go from the Pacific Rim to Japan (about a 1000-mile distance). Kaijus, they found, can swim at about 40 mph. As forces of nature, Kaijus tend to move randomly from their origin point to the nearest landmass. This helped the scientists derive a partial differential equation according to this diffusion and spatio-temporal evolution of the monsters’ density. They also factored in the assumption that the monsters can change direction, especially when encountering a boundary.
Environmental boundary conditions were chosen to be reflective (Neumann) based on the reasoning that while Kaijus can travel by both land and sea, it’s rare for them to go back to the sea once they come ashore. In a worst-case scenario (if, say, aliens sent the monsters to destroy us and kept on sending more of them), the boundary condition would be classed as a source, which the scientists also considered in their equations.
As for initial distribution, since the source of the monster is unknown, the scientists assume the worst: The monsters would run amok on land at carrying capacity, which is the maximum density of life that a region can support.

A theatrical poster for a monster movie. This work is in the public domain because it was published in the United States between 1924 and 1963 and although there may or may not have been a copyright notice, the copyright was not renewed. Unless its author has been dead for the required period, it is copyrighted in the countries or areas that do not apply the rule of the shorter term for US works, such as Canada (50 pma), Mainland China (50 pma, not Hong Kong or Macao), Germany (70 pma), Mexico (100 pma), Switzerland (70 pma), and other countries with individual treaties. See Commons:Hirtle chart for further explanation. Image via Wikimedia Commons.
Now that we know the parameters for their population, which common tactic used in the movies is most effective for getting rid of them? Could it be deploying Jaegers or creating a Kaiju of our own? Either way, Woolley and Maini knew that they needed to take a look at the potential regions we’d be dealing with.
Because this is a fictitious system, the mathematicians approached it “a bit backward” to show what math could do with hypothetical situations. “Do you destroy the population, or does it survive?” asks Woolley. The answer, he says, depends on the area of the population. It also depends on where that population is located: Are the monsters taking over an island, or spreading out over a continent? In order to cover their bases, they decided on three different sizes of land to test each strategy in their simulations: the United Kingdom as the small size, Japan as the middle size, and the Americas (North and South) as the largest landmass.
“What’s interesting about a middle-sized country like Japan,” Woolley says, is that it is close to the “bifurcation point” — the point where the Jaegers could be successful, but could just as easily fail. Perhaps this is why so many movies about giant creatures come from Japan, the mathematical biologists suggest. Based on the results for each region, the mathematicians have a preferred strategy for Japan, as we’ll find out.
2 Strategies for Combating Giant Beasts Using COMSOL Multiphysics®
To see how the Jaeger deployment or Kaiju creation would play out for each of the three regions, the team set up the model and equations required, such as nondimensionalization to predict the domain size, stability analysis, and diffusion-driven instability. “We run small proof of concepts in MATLAB® software,” Woolley explains, “and then, because COMSOL® has the coding needed, we run it through the software” via the LiveLink™ for MATLAB functionality.
Woolley says that COMSOL Multiphysics® has all of the equations they need, as well as the ability to run diffusion equations consistently, quickly, and repeatedly. Plus, the software provides quality assurance. They were also able to put maps of the three regions into the software by importing a picture of the country into MATLAB®, which then generated data that can be used by the COMSOL® software to create the geometry.


A Kaiju (left) and a Jaeger (right). Illustrations courtesy Thomas Woolley.
1. Send in the Jaegers
The first strategy the mathematicians proposed is to deploy giant robots to combat the Kaijus wherever they pop up. Monster movie canon has proven that Jaegers are sturdy and powerful enough to terminate many Kaijus before they fall, and oftentimes one Jaeger is deployed at a time to fend off several monsters. Although they are expensive, hard to construct, and dangerously nuclear, Jaegers can be fully controlled, which makes this option more viable than creating a different monster under certain circumstances.
The robots were modeled as point sinks and fixed where they would patrol to the boundaries of the solution space, in order to minimize human fatalities and see how long it would take to wait for monster encounters, as well as to pinpoint robot location.
After running the Jaeger simulation, the results show that due to the limitations of Jaegers (being dispatched as single fighters fending off many monsters), they would only be able to defend a small country, such as the UK. As shown below, once Jaegers are deployed, they can drastically reduce the Kaiju population in about 24 hours.
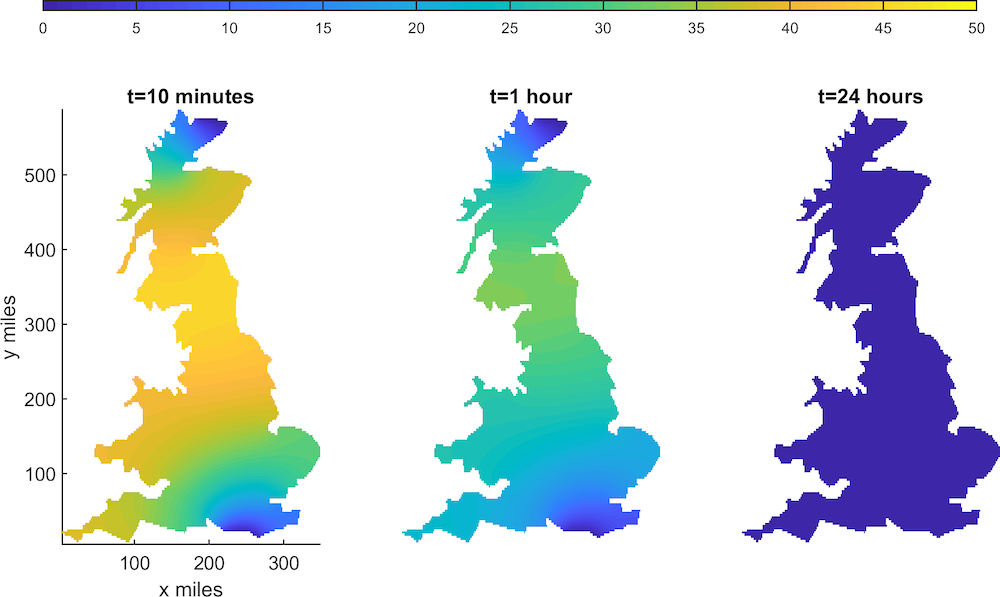
The density of Kaijus over time in the UK with Jaegers posted in the north of Scotland and the south of England. The lighter shaded areas are high population density and the darker areas are the low population density of Kaijus. The scale at the color bar at the top is in thousands of tons. Image courtesy Thomas Woolley.
When it comes to a mid-sized country like Japan, the Jaegers are stretched more thinly. If only given 24 hours, they can still take out a lot of Kaijus, but not completely. If given 70 hours, however, they can reduce the Kaiju population to zero.
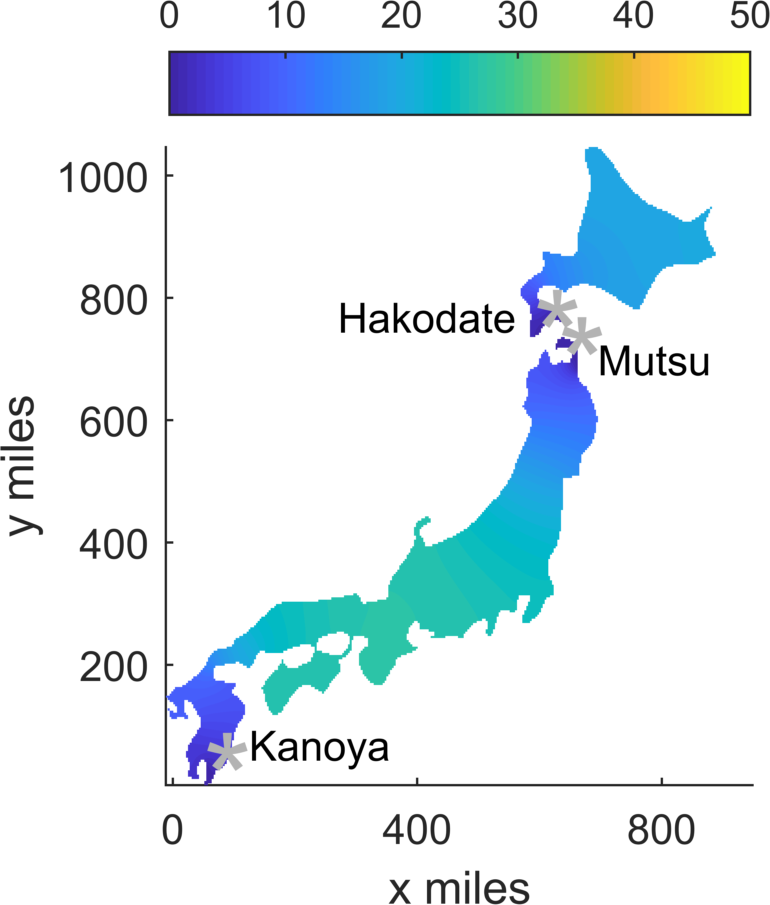
The density of Kaijus over time in Japan with Jaegers posted in the points indicated. In the 24-hour simulation the Kaiju population is stable but not gone.
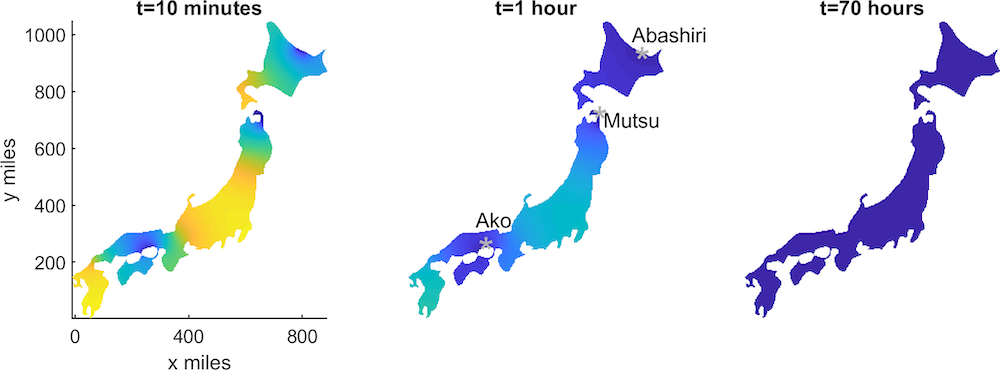
At the end of a 70-hour deployment, however, the Kaiju threat has been eradicated. The scale at the color bar is in thousands of tons. Image courtesy Thomas Woolley.
The results for both the UK and Japan tell us that the Jaegers are good for smaller regions where giant robots could be sent out around the borders and still fight off all the monsters within a reasonable time frame. But due to the small number of robots that would be able to be produced, if the Kaijus are invading an area larger than these islands, another strategy may be required…
2. Create a Bigger Kaiju
The other option is to genetically modify a living creature of our own with radiation (as the movies often depict) to be released among the existing Kaijus. This mutant would have to be stronger than the other monsters and predate on them. However, the mathematicians say to proceed with caution here. Firstly, even the best-trained monsters can still be harder to control than giant robots, and secondly, the new creature as top predator may make the problem worse — in real life, there have been both successful and disastrous cases of this type of ad hoc eradication method of introducing a predator species to a new ecosystem.
With these caveats in mind, the scientists determined that the bigger Kaiju would need to be stronger than the other species of monster, faster, and have a short lifespan — also, it cannot be aggressive to humans. These parameters would allow us to more safely and efficiently send out the mutants over a larger landmass, where they could reproduce and hunt down the existing Kaijus without depending on our control. Furthermore, the mathematical biologists played with kinetics and other parameters to produce spatially heterogeneous spike solutions for our new creatures, meaning that the interactions between predator and prey here would generate a localized and stable ecology so that our monsters will thrive, but only in their localized nests. If these nests are away from human populations, this is a more humane option and we could coexist with them until nature runs its course.
However, after running the simulations, even if our mutants are given the speed and hunting instinct required to hunt down their prey over a large area like a continent, predator-prey equations tell us that the populations would balance out. Increasing the speed of our monsters helps to reduce the number of existing Kaijus, but does not wipe them out completely. The results show that when we increase the speed of our mutants, they are able to employ a kill and corral strategy and move the Kaiju into fewer areas.
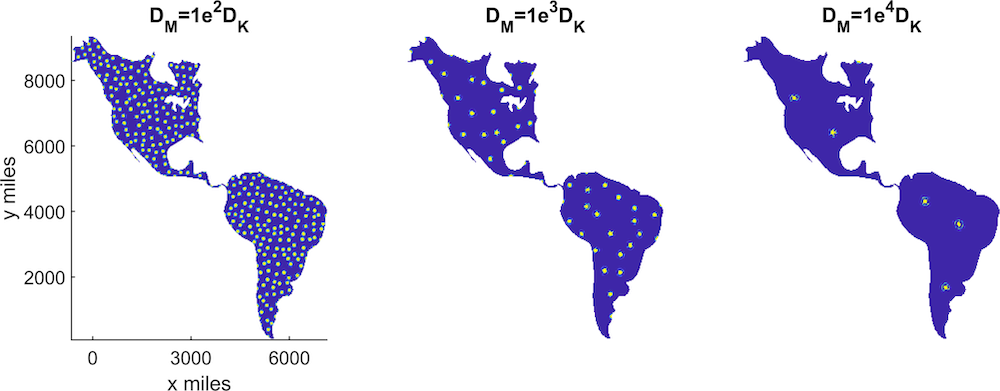
The Kaiju density in North and South America, with dark shading showing low density and light shading showing high density. The speed of our monsters is increased from left to right. Images courtesy Thomas Woolley.
Once the mathematicians saw that this strategy is more effective than Jaegers for a larger landmass, they researched which type of creature would be best to modify, and settled on a moth due to the film history of the giant creature known as Mothra. As it turns out, Mothra has a success record of beating Godzilla. She is both intelligent and aggressive toward the Kaijus, while still being peaceful toward humans. In addition, Mothra’s speed is legendary, and moths live short lives. Thus, Mothra meets the criteria for a modified predator.

Mothra. Illustration courtesy Thomas Woolley.
While each of the strategies the researchers presented depends on the region, they concluded that a combination of strategies would help to clean up the mess once the Kaiju population is at a more manageable state. If our mutants are used to corral the Kaijus into localized areas, we can then deploy the Jaegers to these areas and wipe the Kaijus out to extinction. This will leave our modified monsters without a food source, so they will die out quickly. The scientists do acknowledge that this means our own monsters could prey on humans out of desperation, so it would be in our best interest to implant a kill trigger as a failsafe.
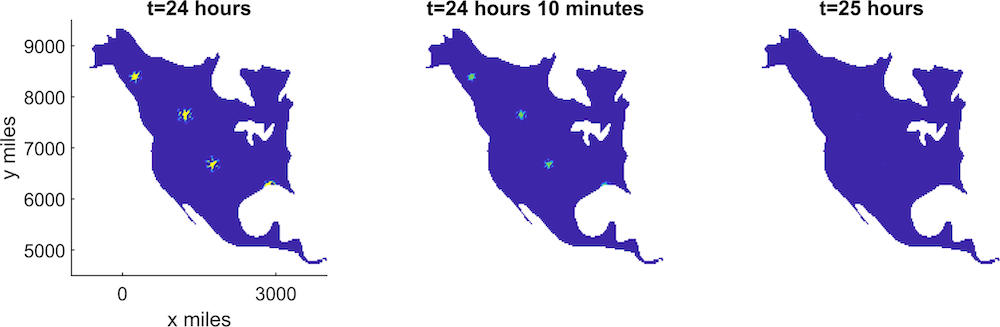
Kaiju hotspots in North America, once our own mutants have rounded up the Kaiju populations. Then, the Jaegers can be sent in to destroy them. From left to right, the Kaiju populations are wiped out over time. Images courtesy Thomas Woolley.
Back to Reality
Using COMSOL Multiphysics, Woolley finds ways to make math more explicable and to mean something to the people he works with. While creating fictional examples is entertaining, Woolley applies his research to the real world as he studies theories of pattern formation and cells. One such project he is working on is calcium signaling and how it sweeps over an egg, looking into how an egg goes from stationary to formation (full-body) using 3D full-wave equations.
In addition, he’s created a graphical user interface (GUI) for spinal tumors, brain imaging, and tumor movement. Like the maps in the fictitious Kaiju scenario, the mathematicians can import the shape of a brain directly into the COMSOL® software for a brain tumor study, a process he calls “fast and easy.”
“COMSOL enables me to go in my own direction without having to construct my own ad hoc code each time,” says Woolley. This frees up time to focus on what matters, whether it’s using mathematical modeling for real-life research or fictitious situations.
Based on the results for the monster invasion, it seems that if we follow the scientists’ tactics, we should be safe — for now. It’s always possible that modifications will have to be made to keep up with future threats. After all, as fictional mathematician Dr. Ian Malcolm says in Jurassic Park, “Life, uh, finds a way.”
Next Steps
Read a related article by Thomas Woolley via The Conversation: “Godzilla, King Kong: films are actually spot on in how to defeat kaijus – mathematician”
MATLAB is a registered trademark of The MathWorks, Inc.





Comments (0)