L’une des questions les plus fréquentes que l’on nous pose est la suivante: Quel est le meilleur moyen d’évaluer des contraintes en présence de singularités? La réponse la plus rigoureuse est d’éviter de le faire. Ce n’est cependant pas d’une grande utilité pratique pour l’ingénierie. Dans cet article de blog, nous examinons les propriétés des champs de contraintes présentant une singularité et nous abordons plusieurs approches possibles.
Ceci fait suite à notre article de blog “Singularities in Finite Element Models: Dealing with Red Spots”, qui décrit quand et pourquoi des singularités de contrainte apparaissent dans les modèles de mécanique des structures. Il propose une introduction générale aux singularités et constitue une première étape recommandée si vous êtes débutant en la matière. Pour des informations détaillées sur la manière de gérer les champs de contraintes avec singularités, poursuivez la lecture ici.
Zoom sur les champs de contraintes présentant des singularités
Commençons par analyser plus précisément un champ de contraintes présentant des singularités et leur relation par rapport aux concentrations de contraintes. Il y a des similitudes, notamment le fait que les concentrations de contraintes apparaissent également au niveau de discontinuités de géométrie. La différence entre une concentration de contraintes et une singularité porte sur le fait que dans la première, la contrainte maximale est bornée. Vous pouvez, par exemple, obtenir une valeur précise en utilisant un maillage suffisamment fin dans un modèle éléments finis (EF).
De façon générale, les concepteurs mécaniques cherchent à réduire les concentrations de contraintes en introduisant des congés présentant le plus grand rayon possible. La contrainte maximale dans une concentration de contraintes est généralement décrite comme étant le produit du facteur de concentration de contraintes K_{\mathrm t} et d’une contrainte nominale convenablement choisie. Pour un congé, l’expression suivante peut parfois être utilisée pour K_{\mathrm t}:
Ici, \rho est le rayon du congé et L_\mathrm{char} est une longueur caractéristique de l’encoche qui se termine dans le congé.
L’équation est basée sur la solution analytique de la concentration de contraintes au niveau d’un trou de forme elliptique dans une grande plaque, avec L_\mathrm{char} la longueur du demi-axe le plus grand de l’ellipse.
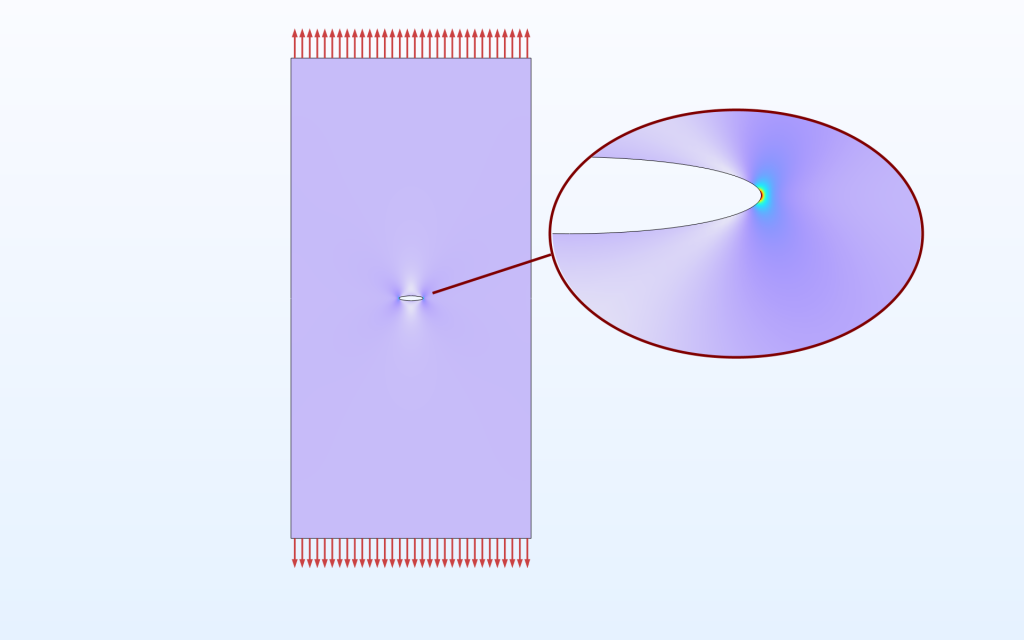
Une grande plaque avec un trou elliptique.
Pour la plupart des encoches, cette expression ne peut être utilisée que pour fournir une estimation grossière de K_{\mathrm t}, étant donné qu’il est difficile d’en déterminer la longueur caractéristique. L’élément à retenir est que la contrainte maximale au niveau d’une petite encoche varie essentiellement avec l’inverse de la racine carrée du rayon du congé. Tout ingénieur ayant tenté de réduire une concentration de contrainte localisée s’est probablement heurté à cela, étant donné qu’une augmentation modérée du rayon du congé induit une réduction de la contrainte maximale encore plus modérée.
Le cas de concentration de contrainte le plus extrême apparaît au fond d’une fissure, où le rayon de l’encoche est infiniment petit. Dans un solide élastique, les solutions des champs de contraintes et de déformations proches du front de fissure sont connues. Ils varient avec l’inverse de la racine carrée de la distance au front de fissure, r. Le champ de contraintes est communément exprimé comme
Ici, K_I, K_{II}, et K_{III} sont les facteurs d’intensité de contraintes pour les mode I (ouverture), mode II (glissement) et mode III (déchirement), respectivement. Les fonctions f, g, et h sont constituées de fonctions trigonométriques de l’angle polaire autour du front de fissure, \theta. (Des instructions détaillées se trouvent ici.)
Une conclusion étonnante est que le champ de contrainte autour du front de fissure est le même, quels que soient la forme réelle de la fissure et le composant dans lequel elle se trouve, tant que l’on est suffisamment proche du front de fissure.
Sous les hypothèses de la mécanique de la rupture en élasticité linéaire, le critère de rupture en mode I est K_I = K_{Ic}, avec K_{Ic} une propriété matériau (appelée ténacité). De cette manière, on peut étudier des géométries avec ce type spécifique de singularité sans utiliser explicitement des contraintes infinies. Ce concept est généralisé dans la suite de cet article.
Considérons désormais un cas où la géométrie présente un élément qui constitue presque une singularité. Par exemple, un coin ou une fissure avec un petit rayon de congé. C’est un scénario sur lequel nous allons nous focaliser dans cet article de blog. A une certaine distance, on ne peut plus vraiment faire la différence entre une encoche et une singularité. L’exemple suivant permet de clarifier le sens de cette affirmation.
On utilise un modèle 2D d’une longue plaque entaillée. En ajoutant des conditions de symétrie le long de l’arête verticale gauche, le même modèle peut être utilisé pour examiner le cas d’une fente interne.
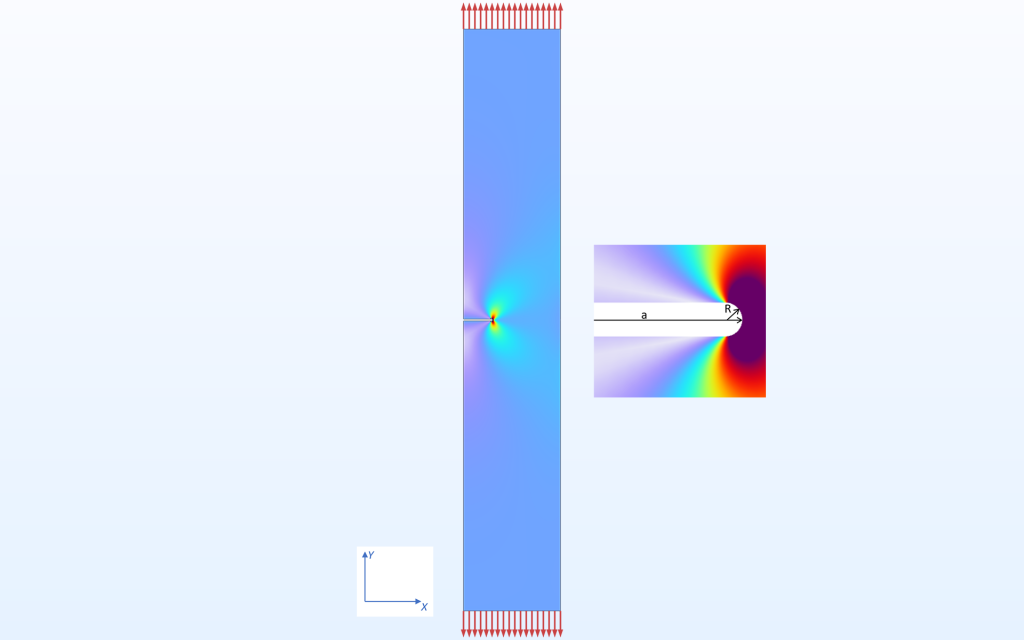
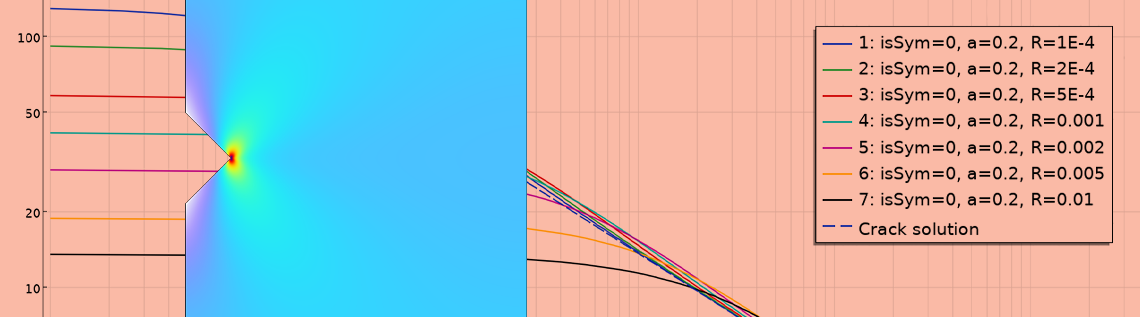
Distribution des contraintes dans une plaque entaillée. Ce modèle est paramétré en fonction de la profondeur d’entaille (a) et du rayon d’entaille (R).
Nous pouvons tout d’abord noter que pour une fissure nette, le facteur d’intensité de contrainte pour cette géométrie s’écrit
Ici, a est la longueur de la fissure; \sigma est la contrainte appliquée (dans ce cas, 1 Pa); et W est la largeur de la plaque. Il existe plusieurs représentations de la fonction f. Nous utiliserons ici l’expression
Cette expression donne ce que l’on appelle la solution du cas avec fissure dans cet article de blog.
La distribution des contraintes le long du ligament (qui s’étend dans la direction x à partir de la pointe de l’encoche) est affichée pour une encoche courte et plusieurs rayons d’encoche. En raison de la symétrie, une seule composante de contrainte, c, est non nulle.
Contrainte verticale le long du ligament en fonction de la distance à la pointe d’encoche pour différents rayons d’encoche. La ligne pointillée montre la valeur théorique pour une fissure ayant la même profondeur.
Il est intéressant d’observer que dans un certain régime, le champ de contraintes ressemble fortement à celui obtenu pour la solution du cas avec fissure. C’est à dire la ligne droite dans le diagramme log(contrainte)-log(distance). En s’approchant de l’encoche, la contrainte est bornée puisqu’il s’agit d’une encoche et non d’une fissure. Comme attendu, la contrainte maximale est proportionnelle à 1/\sqrt{R}.
Loin de la pointe, la solution du champ de contraintes locales du cas fissure n’est plus valide quel que soit le cas, que l’on soit dans le cas d’une fissure ou d’une encoche. Mais dans la zone intermédiaire entre très proche et très loin, que ce soit d’un point de vue visuel ou physique et mathématique, il n’est pas vraiment possible de déduire la forme réelle de la pointe de l’encoche.
Pourquoi est-ce important? Si l’on connait la forme de l’encoche, on peut en fait déterminer la contrainte à cet endroit, simplement en observant la contrainte à une certaine distance. Nous examinerons cette idée plus en détail ultérieurement.
Affichons ensuite les contraintes pour un large éventail de rayons d’encoche et de longueurs d’encoche dans le même diagramme. L’axe horizontal est désormais normalisé par le rayon d’encoche, R.
Contrainte verticale le long du ligament en fonction de la distance à la pointe de fissure pour différentes profondeurs et rayons d’encoche.
Comme on peut le constater ici, le régime avec pente constante est atteint pour une distance à la pointe d’encoche plus petite que le rayon d’encoche, disons 0.7 R. C’est assez proche, du point de vue des problématiques que nous ciblons. A quel point cette région s’étend-elle? Cela n’est pas contrôlé par les détails de l’encoche, mais plutôt par la taille de la géométrie. En utilisant une autre normalisation pour le graphique, la longueur du ligament (W-a), on peut obtenir cette information.
Le même graphique que celui ci-dessus, cette fois avec la distance normalisée par la longueur du ligament.
On peut en conclure que le régime avec pente constante pour ce cas s’étend sur environ 10% du ligament. Plus loin, le champ de contraintes n’est plus contrôlé par la solution du cas avec fissure, mais par des caractéristiques plus globales. La largeur sur laquelle s’étend ce régime pour une géométrie donnée dépend d’une échelle de longueur spécifique à cette géométrie.
Regardons si le champ de contraintes de la solution avec fissure peut être utilisé pour prédire la contrainte maximale au niveau de la pointe de l’encoche. Retournons tout d’abord au cas du trou elliptique dans une grande plaque. Le rapport entre la contrainte maximale au niveau d’un trou elliptique (de largeur a et de rayon d’encoche R) et le facteur d’intensité de contraintes pour une fissure (de longueur a) est
En considérant R << a, la contrainte maximale peut être exprimée à l’aide du facteur d’intensité de contraintes sous la forme
L’idée est donc que lorsqu’un facteur d’intensité de contraintes peut être calculé, il est possible de déterminer les contraintes au niveau d’une pointe d’encoche arrondie en utilisant une expression du type
dans laquelle le coefficient \beta est un nombre dépendant de la configuration, de l’ordre de 1. Nous pouvons tester cette hypothèse sur l’exemple ci-dessus.
Sur les graphiques ci-dessous, l’expression
est tracée en fonction de la profondeur d’encoche, en utilisant le rayon d’encoche comme paramètre. Deux géométries différentes sont utilisées: l’encoche débouchante et la fente centrale. Le dernier cas est obtenu en ajoutant une condition de symétrie au modèle.
Le facteur \beta pour le cas d’une encoche débouchante.

Le facteur \beta pour le cas avec fente centrale.
Comme on peut le remarquer, la valeur du multiplicateur supposé \beta est proche de 1.2 pour les deux cas, tant que le rayon d’encoche est petit. Pour un rayon d’encoche plus grand et de petites longueurs d’encoche, la ressemblance à une fissure n’est pas aussi bonne. La simplification basée sur R << a n’est pas valide.
Pour produire ces graphiques, nous avons utilisé la valeur analytique de K_I. Pour un cas réel où celle-ci n’est pas connue, les solutions à une certaine distance de l’encoche peuvent être utilisées pour déterminer K_I numériquement.
En réalité, pour tout angle vif, il existe une région dans laquelle le champ de contraintes décroît en r^{-p}, avec r la distance à l’angle. Jusqu’ici, nous avons vu que pour une fissure idéale, p = 0.5. La valeur de p pour n’importe quel angle d’ouverture est affichée sur le diagramme ci-dessous.

Puissance de la décroissance de la contrainte avec singularité pour différents angles d’ouverture. Les valeurs pour 45°, 90°, et 135° sont mises en évidence.
La courbe a été tracée en résolvant l’équation transcendante \sin \left ((1-p)(2\pi-\alpha) \right) +(1-p) \sin(2\pi-\alpha) = 0, dans laquelle \alpha est l’angle d’ouverture.
Par souci d’exhaustivité, nous pouvons vérifier la solution de l’équation transcendante dans un modèle EF de la plaque en traction comportant un angle rentrant. Le modèle est paramétré en utilisant l’angle d’ouverture de l’angle rentrant.

Les contraintes de von Mises dans le modèle avec angle rentrant, dans le cas où l’angle d’ouverture est de 90°.

Contrainte verticale le long du ligament. La distance à la pointe de l’angle rentrant est normalisée par la longueur du ligament. Les lignes pointillées montrent les solutions théoriques, utilisant les valeurs de p trouvées ci-dessus.
Comme nous pouvons le remarquer, il y a des régimes avec des lignes presque droites dans le diagramme contraintes-distance, qui au voisinage de l’angle rentrant sont en bon accord avec les pentes théoriques.
Un autre type de singularité est engendré par une discontinuité de matériau. En pratique, cela se produit souvent de façon conjointe à une singularité géométrique. Limitons-nous ici à l’étude d’une discontinuité de matériau seule dans une barre soumise en traction.
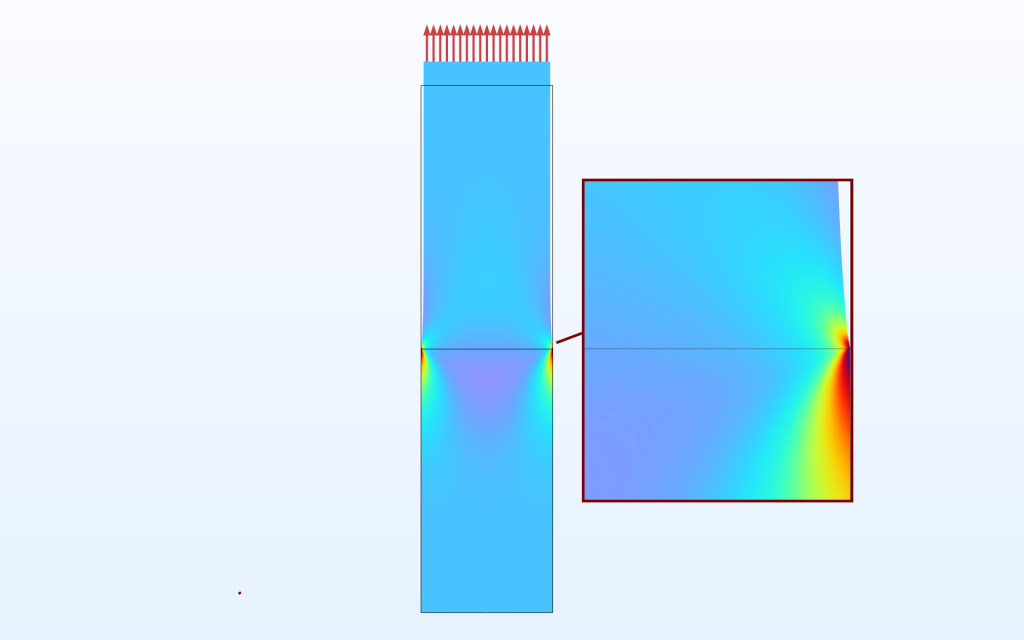
Une barre dont la partie inférieure est plus rigide que la partie supérieure. La contrainte dans la direction du chargement est affichée.
Ce premier graphique permet d’ores et déjà de dégager des propriétés générales:
- Une singularité apparaît au niveau de la surface libre.
- La contrainte est plus élevée dans le matériau rigide qu’au niveau de la localisation correspondante dans du matériau souple.
Pour examiner cela plus en détail, nous pouvons créer des graphiques montrant la décroissance de la contrainte en fonction de la distance à l’interface entre les matériaux.

Contrainte dans la direction de chargement affichée le long des frontières libres, en fonction de la distance à l’interface. Les lignes continues représentent les résultats dans le matériau souple, tandis que les lignes pointillées représentent les résultats dans le matériau rigide. Le paramètre r est le rapport des deux modules d’Young.
Nous pouvons là aussi identifier des lignes droites dans le diagramme log–log, indiquant que la contrainte varie avec la distance en r^{-p}. La puissance ‘p’ est la même dans les deux matériaux (les lignes continue et pointillée de la même couleur sont parallèles). L’intensité de la singularité est contrôlée à la fois par le rapport entre les deux modules d’élasticité et par les valeurs des coefficients de Poisson.
En regardant la déformation (exagérée) de la forme du graphique de surface ci-dessus, on peut l’interpréter physiquement de la façon suivante: Le matériau plus souple va, pour le même chargement, s’étendre plus que le matériau plus rigide. Cela signifie que les déformations dans la direction du chargement seront plus grandes dans le matériau plus souple. Cela signifie également qu’il y aura une contraction correspondante plus importante dans la direction transverse, les deux matériaux ayant le même coefficient de Poisson. Cette contraction sera toutefois entravée au niveau de l’interface entre les deux matériaux, engendrant une singularité locale pour les contraintes.
En choisissant
cette singularité disparaît complètement.
Pour conclure, une transition matériau va, dans la plupart des cas, engendrer une singularité. Dans ce cas, il y a également une zone au voisinage de la discontinuité dans laquelle la contrainte décroît selon une loi puissance.
Nous avons étudié les cas les plus courants de singularités qui peuvent apparaître dans des modèles EF, et nous avons vu qu’ils ont une propriété en commun: Les contraintes au voisinage de la singularité ont une dépendance à la distance suivant une loi puissance.
Evaluation des soudures
La conception de soudures sûres en matière de fatigue est un domaine important de l’ingénierie. Beaucoup d’efforts ont été déployés pour fournir des méthodes systématiques de prédiction de défaillances, même si une évaluation précise des contraintes est généralement impossible. Dans ce cas, c’est surtout le fait que la géométrie exacte de la soudure soit inconnue qui pose problème. Selon la géométrie locale exacte, la soudure peut induire ou non une singularité au niveau des contraintes. Pour ajouter à la complexité de la question, il y a souvent des défauts cachés dans les soudures. A l’exception des situations où une très haute qualité est nécessaire, auquel cas la soudure peut être rectifiée et vérifiée à l’aide de méthodes de contrôle non-destructif. Dans la plupart des cas cependant, il n’est pas pertinent de réaliser une analyse détaillée des contraintes locales dans la soudure.

Une soudure d’angle, mais trois géométries locales distinctes.
Une introduction à l’évaluation des contraintes dans les soudures est donnée dans notre article de blog “How to Predict the Fatigue Life of Welds”.
Plutôt que d’entrer dans les détails de l’analyse des soudures, c’est la philosophie de conception qui est intéressante ici:
- Calculer les contraintes à un endroit bien spécifique, pas au niveau de la soudure elle même.
- Etablir les valeurs autorisées pour ces contraintes. Cela se fait généralement de manière expérimentale.
- La valeur de contrainte autorisée dépend de l’endroit choisi et de la façon dont les contraintes sont évaluées, ce n’est donc pas une propriété matériau en tant que telle.
A l’époque où l’on réalisait les calculs avec une feuille et un crayon, tous les effets locaux étaient ignorés. Les valeurs de contraintes autorisées prenaient cela en compte et étaient de fait assez basses. Les approches modernes basées sur la méthode des éléments finis prennent une partie des concentrations de contraintes en compte (la partie engendrée par la géométrie globale, mais pas celle liée à la géométrie locale de la soudure). Les contraintes autorisées peuvent donc être supérieures, mais sont toujours significativement plus basses que celles qui pourraient être données par un essai mécanique sur matériau pur.
En termes d’éléments finis, un modèle de coque renverrait généralement les contraintes recherchées, tandis qu’un modèle de mécanique du solide capturerait des détails concernant les contraintes qui ne sont pas souhaitables pour conduire une analyse de la soudure en fatigue.
Approches suggérées
Il y a plusieurs raisons fondamentales différentes pour lesquelles votre modèle EF peut contenir des singularités. Par exemple:
- Les conditions aux limites génèrent des singularités, comme cela est traité dans l’article de blog mentionné plus tôt. Si des singularités telles que celles-ci posent problème dans l’analyse, cela peut être réglé en raffinant les conditions aux limites.
- Un angle vif est introduit car l’échelle de la géométrie locale ne permet pas de modéliser raisonnablement un congé à l’échelle globale. Dans ce cas, il n’y a pas vraiment une singularité, mais plutôt une concentration de contraintes bien définie. L’approche la plus rigoureuse consiste à utiliser une technique de submodeling pour déterminer l’état de contraintes locales en s’appuyant sur la solution globale. Dans le modèle global, vous pouvez utiliser l’amplitude de la décroissance en loi puissance du champ de contraintes au voisinage de la concentration de contraintes pour savoir où concentrer vos efforts. Une autre possibilité est de combiner votre connaissance du champ de contraintes proche à la façon dont il est corrélé à une concentration de contraintes locales pour parvenir à estimer la concentration de contraintes locales.
Vous pouvez suivre la tendance de l’évaluation de soudures et l’adapter à vos conditions locales. Pour cela, vous aurez besoin d’une vaste base d’expériences sur laquelle vous reposer. Parmi les designs antérieurs, lesquels ont présenté des défaillances, lesquels n’en ont pas présentées ? Vous devrez ensuite analyser les designs antérieurs et tenter de trouver une méthode d’évaluation corrélée à l’expérience.
Commencez par mettre en place un modèle EF de ces designs et tentez d’identifier une zone dans laquelle le champ de contraintes ou de déformations est dans l’intervalle qui n’est ni contrôlé par les détails locaux de l’encoche, ni par la géométrie plus globale. Il sera peut-être nécessaire d’utiliser une méthode de submodeling, tout du moins pour développer le critère.
Le choix du critère n’est généralement pas évident. Etant donné que vous réaliserez seulement des comparaisons relatives, et que vous ne relierez pas les données calculées à une quelconque valeur physique de résistance, il y a de nombreux choix possibles. En voici quelques exemples:
- La quantité doit être simple à évaluer.
- La quantité ne doit pas être trop sensible aux incertitudes de l’analyse.
- Si possible, la quantité doit être physiquement pertinente. Par exemple, si le matériau est fragile, il sera préférable de regarder la plus grande contrainte principale ou déformation principale plutôt qu’utiliser un critère de contraintes équivalentes tel que celui de von Mises.
- Si la fatigue est une problématique, la quantité doit être sensible aux inversions de chargement.
- Si possible, sélectionnez un critère de déformations plutôt qu’un critère de contraintes. Cela est lié au fait que les déformations sont calculées en utilisant les déplacements directement, tandis que les contraintes sont calculées en s’appuyant sur une combinaison des déplacements. Cela signifie qu’une seule composante erronée dans le tenseur de déformations se propage dans l’ensemble des éléments du tenseur de contraintes.
- Dans le logiciel COMSOL Multiphysics® vous pouvez utiliser la fonctionnalité Safety pour évaluer un large éventail de critères différents, y compris des critères personnalisés.
En règle générale, la puissance caractérisant la singularité n’est pas connue. En revanche, nous savons que dans une zone donnée, la quantité d’intérêt varie selon la forme
On peut obtenir les valeurs de K et p par la méthode des moindres carrés ou en utilisant simplement les valeurs de deux points sur la ligne droite dans un diagramme log–log. Etant donné que p doit être constant pour un type de singularité donné, on peut se servir de sa valeur calculée pour contrôler la validité de l’approche.
Une fois p connu, c’est la valeur de K pour une configuration donnée qui doit être comparée à une valeur autorisée. C’est par analogie la façon dont les fissures sont traitées en mécanique de la rupture.
La méthode des percentiles
Une autre approche pour obtenir les niveaux de contraintes autorisés consiste à définir une contrainte de référence comme étant la valeur qui est dépassée dans une certaine fraction (par exemple, 5%) d’un volume de référence. Si cette contrainte de référence est plus basse que la valeur autorisée, le design est accepté. En utilisant cette approche, on évite la problématique de l’évaluation à proximité de singularités. Il suffit d’être en mesure de calculer le volume dans lequel la contrainte de référence est surpassée, et que les frontières de ce volume soient à une certaine distance de la singularité, où la solution a bien convergé.
Cette méthode semble simple, mais nécessite une certaine standardisation pour être appliquée. L’un des problèmes ici est de déterminer le volume de référence. Si le volume total de la structure est utilisé, il sera possible de faire baisser la contrainte de référence en ajoutant plus de matériau dans la région à faibles contraintes, ce qui n’a bien sûr pas de sens. Le volume de référence doit être lié, par exemple, à la taille de la zone spécifique autour de la singularité. Un autre inconvénient porte sur le fait que les méthodes d’optimisation pourraient choisir de déplacer les contraintes de manière à diminuer la contrainte de référence tandis que la contrainte maximale augmente.
Encore une fois, on ne peut que comparer des structures similaires entre elles.
Regardons à présent comment évaluer les contraintes en utilisant la méthode des percentiles. Dans COMSOL Multiphysics®, il n’est pas possible d’évaluer directement la valeur de contrainte à 5%. Trois méthodes alternatives sont décrites ci-dessous.
Méthode 1
Si l’on a besoin que d’une évaluation, la technique la plus rapide consiste généralement à réaliser quelques itérations manuelles. On crée simplement un opérateur d’intégration (disons intop1), et on évalue une expression du type intop1(solid.mises>sRef)/intop1(1). En modifiant la contrainte de référence, sRef, à quelques reprises, on trouve rapidement la valeur correspondant au percentile donné.
Méthode 2
Utiliser une méthode de modèle pour automatiser la Méthode 1.
Méthode 3
On peut implémenter une équation supplémentaire et résoudre la valeur de contrainte, comme expliqué ci-dessous.
L’équation à résoudre est la suivante:
Où \sigma_\mathrm{c} est la contrainte calculée. Cela peut être une contrainte équivalente comme von Mises, une première contrainte principale, ou autre chose. On pourrait bien sûr utiliser la même procédure pour un critère en déformation ou un critère énergétique. Le volume de référence est noté V_\mathrm{ref}, et \beta est le percentile. L’expression booléenne dans l’intégrale est supposée égale à 1 lorsqu’elle est vraie et 0 lorsqu’elle est fausse.
Pour avoir une mise à l’échelle plus simple à gérer pour les calculs, il est préférable de réécrire l’équation sous la forme suivante
L’intégrale peut être calculée à l’aide d’un opérateur d’intégration, comme cela est fait dans la première méthode. Un moyen direct d’implémenter cette équation en utilisant un noeud Equation globale est montré ci-dessous:
Malheureusement, cela ne fonctionnera pas. Une inégalité n’est pas différentiable, on ne peut donc pas assembler de Jacobienne. La matrice de raideur contiendra uniquement des zéros pour cette équation. On peut cependant contourner le problème en introduisant une dérivée manuelle par différences finies. L’expression est assez longue, et requiert une certaine compréhension de la modélisation via les fonctionnalités mathématiques de COMSOL®, une explication détaillée est donc donnée dans la section Informations complémentaires ci-dessous.
Ci-dessous se trouve l’équation globale modifiée qui permet de résoudre la problématique consistant à trouver la contrainte qui donne le percentile désiré.
Ici, le paramètre défini par l’utilisateur dS est un incrément sur la contrainte, noté \Delta \sigma dans la section Informations complémentaires.
Pour illustrer cette approche, on utilise la même plaque avec encoche que dans l’exemple précédent. Etant donné que le volume de référence doit être indépendant de la taille de la plaque, on peut, par exemple, choisir un cercle autour de l’encoche. Dans ce cas, le rayon du cercle peut être basé sur les longueurs caractéristiques suivantes de la structure:
- Largeur: 1 m
- Longueur de fissure minimum: 0.1 m
- Largeur de ligament minimum: 0.3 m
- Rayon d’encoche maximum: 0.01 m
Un volume de référence basé sur un cercle de rayon 0.05 m autour de la pointe de l’encoche sera éloigné des frontières de la structure, mais également éloigné des détails de l’encoche elle-même.

Le niveau de contrainte qui est dépassé dans 5% du volume de référence pour différentes valeurs de profondeur d’encoche et de rayon d’encoche.
Pour toutes les valeurs de profondeur d’encoche, le 5e percentile de contraintes est généralement indépendant du rayon d’encoche. Il est uniquement sensible à la profondeur d’encoche. Cela est cohérent avec l’idée de fond: Eviter la sensibilité aux détails d’un champ de contraintes local, présentant d’éventuelles singularités. Les mêmes résultats sont obtenus avec une extrémité effilée ou arrondie. De façon générale, cette approche donne la même information qu’un facteur d’intensité de contraintes: une mesure de l’intensité de la singularité. Si des structures possédant le même type de congés sont comparées, cette méthode peut fournir un critère adéquat.
Informations complémentaires
Cette expression contient deux termes: Le premier crée le résidu, et le second crée la Jacobienne. C’est une solution qui peut généralement être utilisée en modélisation avancée. Si, par exemple, une Jacobienne exacte est coûteuse à créer, vous pouvez utiliser des expressions similaires pour former un résidu correct combiné à une Jacobienne approximative.
L’opérateur nojac(expr), qui est utilisé à plusieurs reprises, assure que l’expression donnée ne génère pas de contribution à la Jacobienne.
Le terme de la Jacobienne est multiplié par le facteur (sRef-nojac(sRef)). Etant donné que cette expression est toujours nulle, aucun résidu ne sera généré par cette partie de l’expression. La dérivée de sRef par rapport à elle-même est simplement 1, et le reste de l’expression est une expression de la dérivée par différences finies centrée.
Ici, \Delta \sigma est une variation finie de la contrainte. Elle doit être choisie de façon à être aussi petite que possible tout en permettant que le volume calculé par \displaystyle \int_V (\sigma_\mathrm{ref}+\Delta \sigma<\sigma_\mathrm{c}) \; dV soit significativement différent de \displaystyle \int_V (\sigma_\mathrm{ref}<\sigma_\mathrm{c}) \; dV . Un bonne valeur est lorsque la variation de contrainte sur un élément est de \Delta \sigma au voisinage de l’isosurface de la contrainte de référence résultante \sigma_\mathrm{ref}.
Pour conclure
Même s’il est impossible, d’un point de vue théorique, d’évaluer des gradients et des flux (déformations et contraintes) au niveau d’une singularité, il existe des méthodes systématiques grâce auxquelles on peut approcher le problème. Ce type de méthode requiert toutefois d’avoir suffisamment de données expérimentales permettant d’interpréter une quantité critique choisie de façon judicieuse.
Pour télécharger les modèles utilisés dans cet article de blog, cliquez sur le bouton ci-dessous.



Commentaires (0)