
The Beckham and Maradona curl obtained with the inside of the soccer cleat (football boot), and the curl by Eder, Nelinho, and Roberto Carlos with the outside of the cleat, is due to the Magnus effect. The effect is named after the scientist who first observed it in a laboratory in the 1850s. The Magnus effect explains the side-force on a sphere that is both rotating and moving forward. We’ll use it to analyze the FIFA World Cup™ match ball.
Where Sports Meet Engineering
Like many kids around the world, my dream was to become a professional soccer player, or football as it’s called outside the U.S., Canada, and Australia. However, as a nerdy kid, I also had two other main interests: cars and science.
I remember being obsessed with the aerodynamics of cars in the early 1980s. In particular, the drag coefficient in competition and revolutionary aerodynamic designs between Audi and Ford. I was also keen to understand and achieve the specific curl of the ball when violently hitting it with the outside of my cleat. Engineering science was the glue that unified these interests later in life. Now, in preparation for the FIFA World Cup™, I will share some of my CFD analyses of the match ball with you.
Spin and Lack of Spin
The spinning of the ball has a stabilizing effect on the flow around it and thereby on its trajectory. But, let’s begin with a case where there is little or no spin.
If there is no spin, a Karman vortex street is formed behind the ball. The ball will then be subjected to force fluctuations with the detachment of vortices behind it. The wakes formed behind the ball not only increase the drag, they also contribute to the swerves that can be observed by anybody who has kicked a beach ball or been in the flight path of a knuckleball thrown by a baseball player. This semichaotic pattern can be partially explained in a transient simulation using the CFD Module.
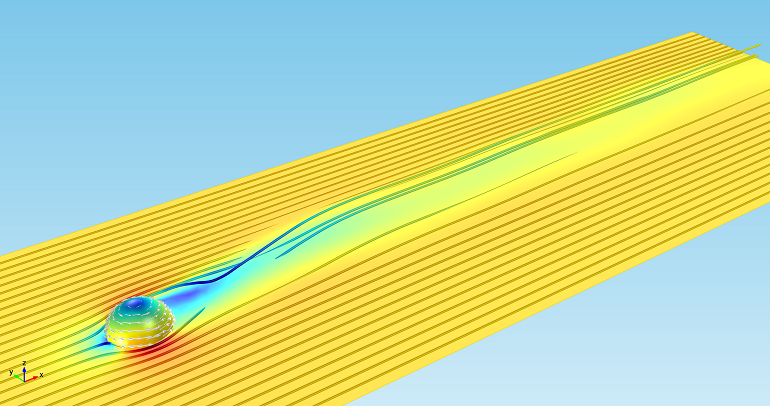
The figure and animation below show the Karman vortices behind a ball rotating counterclockwise with the same velocity at the equator as its forward movement, i.e., at the relatively low spin value. The animation is recorded on a corresponding 2D problem of a cylinder, which qualitatively shows the same effect.
Spin and the Magnus Effect
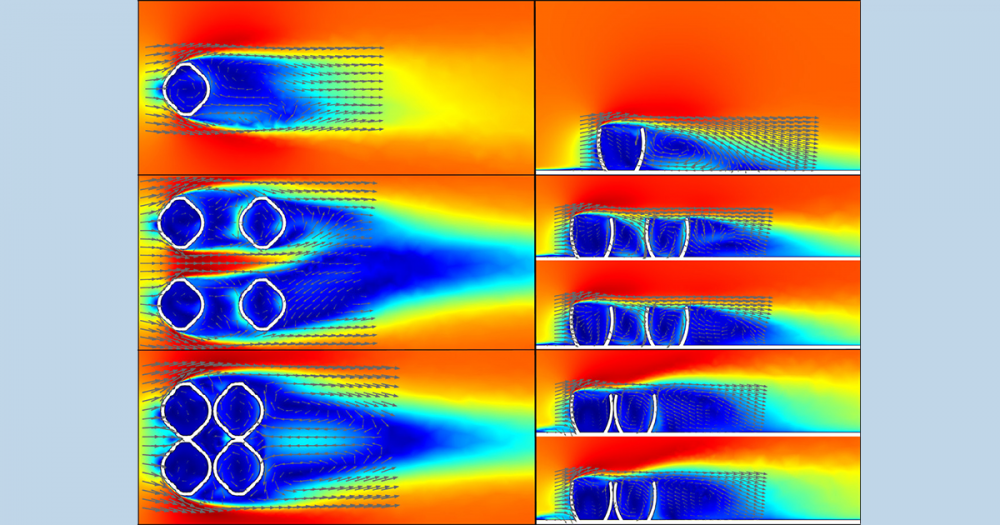
As the rotation velocity increases, the stagnation points on the ball move together and eventually outside its surface. At this point, the velocity due to the rotation of the ball is perfectly balanced by the ball’s forward movement [1]. If it were not for the fact that the ball loses some of its momentum due to friction, there would be a steady solution for this problem, which is in contrast to the case of the lower spin value discussed above. At this stage, the flight of the ball is stabilized and is much more predictable — at least for the player shooting the ball or the goalie.
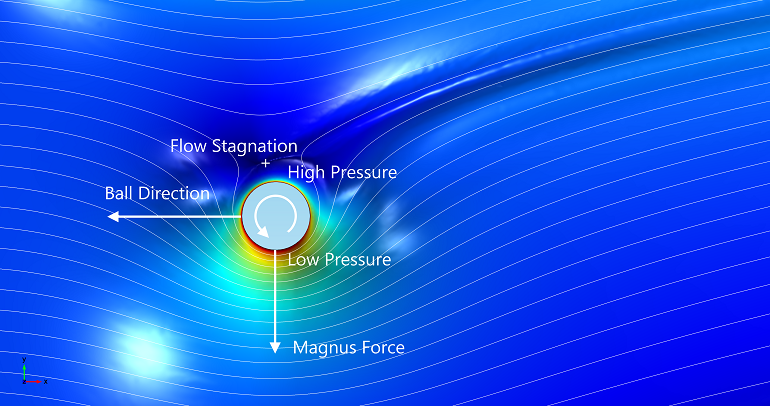
The figures below show the velocity and pressure fields around the rotating forward-moving ball and a rotating cylinder. The velocity at the equator is much higher on the side of the ball that rotates and slides the air past its surface. On the other side of the ball, the ball’s rotation and the air that has to pass the ball work against each other.
Due to the difference in speed and shear between the two sides of the ball, a pressure difference is also built up between the two sides. This causes a force that sucks the ball towards the side where the air velocity is higher, which is the Magnus force acting on the ball. This is also reflected in an increased lift coefficient with the spin.

Turbulence and FIFA World Cup™ Match Ball Design
Although the simulations I shared above help explain the Magnus effect, there is more to the flight of a soccer ball than the simulations under ideal laminar conditions. Being the center of attention in the most popular sport in the world, the ball and its design have been the subjects of plenty of research. Since the release of the Adidas® Jabulani for the FIFA World Cup 2010™ in South Africa, this research has become even more intense due to the ball’s revolutionary design.
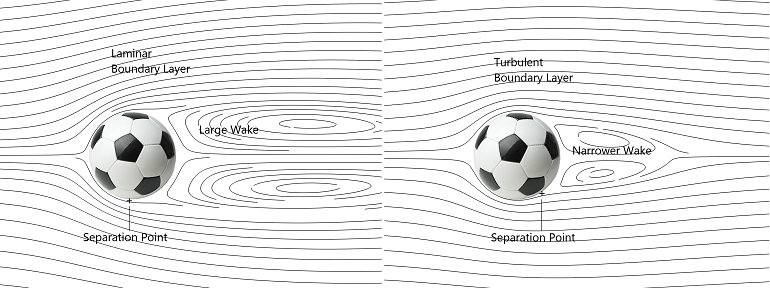
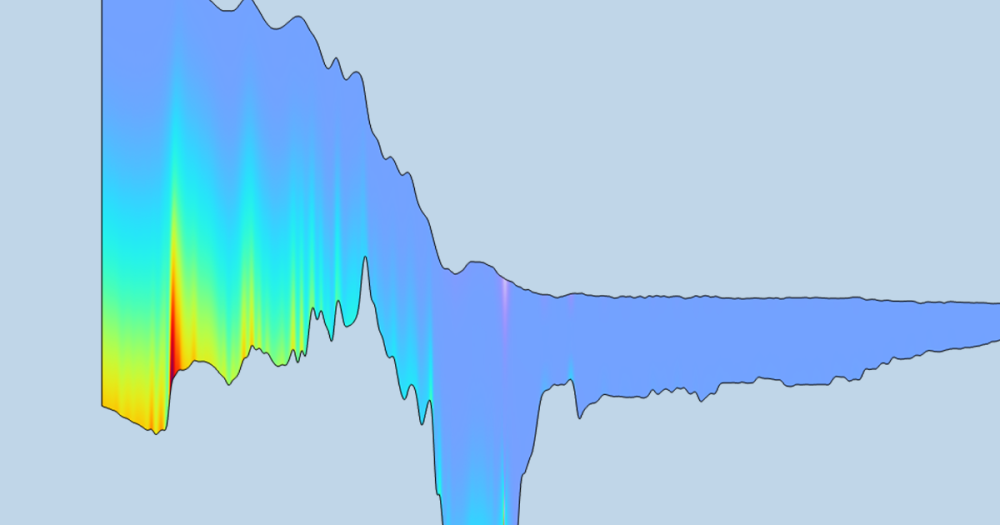
The high drag coefficients for laminar flow are caused by boundary layer separation forming a low-pressure wake that slows down the ball in this flow regime. For higher flight velocities, the boundary layer becomes turbulent ahead of the separation point and remains attached further downstream on the rear side of the ball before the flow reverses. This leads to a narrower wake and a correspondingly lower drag coefficient. The phenomenon is generally referred to as the drag crisis, which is illustrated below.
The traditional soccer ball (shown above) has 32 panels: 20 regular hexagonal and 12 regular pentagonal panels. The Jabulani, on the other hand, had eight panels, as you can see in this finite element impression of the match ball:

The reduced number of the seams, shown in black, was compensated with grooves that roughened the surface. However, the aerodynamic properties of the Jabulani were quite different from the traditional ball.
The fact that the panels and seams were fewer and shallower on the Jabulani, compared to those on a traditional ball, increased the laminar flow region with high drag coefficients, while it decreased its drag coefficients at higher speeds. The relatively large width of the laminar regime compared to that of a traditional ball gave it the behavior of a beach ball for a wider velocity range, which was the subject of complaints from many goalies. Also, the pattern that the ball presents to the wind has an impact on the sudden changes in direction for these “knuckleball” kind of shots [2].
The Adidas Brazuca®, the official ball for the FIFA World Cup 2014™ in Brazil, has only six panels. However, the total length of the seams is comparable to that of a traditional ball. Additionally, the depth of the seams is larger than for the Jabulani.
The drag coefficient as a function of the Reynolds number for the Brazuca® is, therefore, more similar to that of a traditional ball, as you can see in the graph below. Thus, the ball is expected to have a stable flight over a wider range of velocity due to the turbulence caused by the seams.

Enjoying the Effects of the Lack of Spin, Spin, Turbulence, and the Magnus Effect
In association football, players like Ronaldo can hit a ball hard and consistently without spin, giving it a straight path far from the goal. That is due to turbulence and the swerving chaotic trajectory closer to the goal, when the flow starts to become laminar.
In contrast, the stable curl of the spinning ball, due to the Magnus effect, allowed players like Beckham and Maradona to repeatedly place a 30-meter cross within a radius of half a meter from the target.
The very hard hit together with the spin that Eder, Nelinho, and Roberto Carlos use, in combination with the transition between laminar and turbulent flow, can give the ball an ordered but peculiar trajectory, almost like a guided missile.
Right after impact with the outside of the cleat, when the ball has been accelerated to its top speed, turbulence around the ball and its small drag coefficient gives it a relatively straight trajectory. When the ball slows down, the relative spin becomes stronger and the Magnus effect becomes more pronounced. In other words, the ball first goes straight and then curves suddenly closer to the goal.
This combination of turbulence and the Magnus effect is observed in Roberto Carlos’ famous free kick in the game between Brazil and France in 1997. France’s goalkeeper, Barthez, did not even move until it was too late and a ball boy standing several meters from the goal ducked his head. Both keeper and ball boy thought the ball was going far outside the post!
Tip: You can confirm that this goal was not a coincidence in this YouTube video clip.
More incredible goals featuring the Magnus effect can be found in this clip, where players such as Messi, Ronaldo, Ibrahimovic, Ronaldinho, Beckham, Eder, Cruyff, and many others make use of this effect to cheat the goalkeepers.
Cars, Science, and the FIFA World Cup™ Match Ball
In the early 1980s, car ads always featured the car’s drag coefficient. I have always wondered why this relevant measure disappeared from the published specifications for cars. Now, I can instead think of the curves for the drag and lift coefficients for the ball and picture their combination with the Magnus effect. Imagine that while you watch the incredible shots and goals in this year’s FIFA World Cup™.
Next Steps
Learn more about the CFD Module, an add-on to the COMSOL Multiphysics® software, which provides tools for modeling fluid flow analysis.
Additional Resources
- G. K. Batchelor, “An Introduction to Fluid Dynamics”, Cambridge University Press, ISBN 0 521 09817 3, see plate 12 at page 364 and forward and pages 424–427.
- J. E. Goff, “A Review of Recent Research into Aerodynamic of Sport Projectiles”, Sports Eng (2013), 16:p137–154.
- Download the model: The Magnus Effect
- Check out several other posts about the physics of sports on the COMSOL Blog
Adidas and Brazuca are registered trademarks of adidas AG. COMSOL AB and its subsidiaries and products are not affiliated with, endorsed by, sponsored by, or supported by adidas AG.
FIFA World Cup, 2014 FIFA World Cup, and 2010 FIFA World Cup are trademarks of FIFA. COMSOL AB and its subsidiaries and products are not affiliated with, endorsed by, sponsored by, or supported by FIFA.



Comments (6)
Lingling Tang
June 15, 2014It seems that a newly released “magnus_effect_3d” mph file is added to The Magnus Effect model, and the 3d model is more vivid and fantastic.
Jonathan Nyquist
June 30, 2014An example that truly deserves to be called awesome!
Masaaki KOJIMA
August 22, 2014Hello!!
My name is Kojima@KESCO.
This article has been quoted in the Japanese article of Gigazine site as below URL.
URL: (in Japanese text only)
http://gigazine.net/news/20140619-magnus-effect-world-cup-ball/
Fanny Littmarck
August 25, 2014Thanks for sharing, Kojima.
Charles CRUMMER
July 7, 2016The Magnus effect is caused by the rotating ball carrying the boundary layer into the flow on the side of the ball rotating into the flow. This results in an increase of pressure there. That’s why the design of the ball’s surface is so important. For example, fuzzy tennis balls exhibit the effect better than bald ones. I have written a paper discussing subsonic aerodynamics at the particle level here — arXiv:nlin/0507032. I’d like to get some feedback about my conclusions and reasoning. Thanks.
Debopam Das
April 12, 2021The observed effect should be called Robins effect or at least Robins-Magnus effect. Long before discovery of Magnus in 1852, Benjamin Robins explained the phenomena in Principles of Gunnery (1742). Scientific community should correct the history. We must rename Magnus effect as Robins-Magnus effect at least. Interestingly, Robins considered Cannon ball and this article consider football. Magnus considered cylinder.