Simulation micromagnétique avec COMSOL Multiphysics^®

La dynamique de la magnétisation dans les aimants est décrite par la théorie micromagnétique, régie par l’équation de Landau-Lifshitz-Gilbert. Nous avons créé un « module Micromagnetics » sur-mesure à l’aide du Constructeur de physiques du logiciel COMSOL Multiphysics^® qui peut être utilisé pour effectuer des simulations micromagnétiques au sein du logiciel COMSOL^®. Ce module Micromagnetics peut être facilement couplé à d’autres modules complémentaires pour réaliser des simulations micromagnétiques multiphysiques incluant notamment les couplages magnéto-dipolaire, magnéto-élastique et magnéto-thermique. Le module, accompagné d’un guide d’utilisation, est disponible en libre téléchargement.

Introduction à la magnonique et à la micromagnétique

La magnonique est un sous-domaine de la spintronique ou du magnétisme (Réf. 1). Elle est semblable à ses homologues que sont la phononique et la photonique mais se concentre sur le transport d’énergie et d’informations par les ondes de spin (ou magnons dans la limite quantique), qui sont des excitations élémentaires des systèmes magnétiques. Les ondes de spin peuvent transporter de l’énergie, du moment linéaire et angulaire ainsi que des informations. En raison de leur très faible atténuation et de l’absence de chauffage par effet Joule (Réf. 2), les isolants magnétiques tels que le YIG (Y₃Fe₅O₁₂) constituent des matériaux idéaux pour la manipulation des ondes de spin. De plus, les ondes de spin peuvent interagir avec des textures magnétiques (Réf. 3) telles que les parois de domaines magnétiques, les vortex et les skyrmions, offrant ainsi une nouvelle voie pour le fonctionnement des mémoires magnétiques. Cela fait de la magnonique un candidat prometteur pour la prochaine génération de technologies de l’information.

Dans cet article de blog, nous allons expliquer comment utiliser le module Micromagnetics pour réaliser des simulations micromagnétiques numériques de la dynamique des ondes de spin dans COMSOL Multiphysics^®.

Théorie de la modélisation micromagnétique

La dynamique des moments magnétiques dans les matériaux magnétiques est régie par l’équation de Landau-Lifshitz-Gilbert (LLG). Le principe de la modélisation micromagnétique consiste à traiter tous les moments magnétiques d’une ou plusieurs cellules unitaires comme un macrospin semi-classique, représenté par un vecteur unitaire \textbf{m} défini comme suit :

où \textbf{M}(\textbf{r}, t) est la fonction de distribution spatio-temporelle de la magnétisation totale et M_s est la magnétisation de saturation du matériau.

L’évolution temporelle de ce vecteur de moment unitaire suit l’équation LLG (Réf. 4) :

où le point indique la dérivée temporelle, \gamma est le rapport gyromagnétique, \alpha est le coefficient d’amortissement de Gilbert et H_{\rm{eff}} est le champ effectif exercé sur le moment local, qui est défini comme suit :

avec \mu_0 la perméabilité du vide et E l’énergie libre du système magnétique, incluant toutes les interactions possibles.

Supposons le cas le plus simple : un macrospin dans un champ magnétique statique appliqué selon la direction z. Le champ effectif est alors simplement H_{\rm{eff}}=H \hat{e}_z. A partir de l’état initial où le macrospin est légèrement incliné par rapport à la direction d’équilibre z, le vecteur macrospin effectue alors une précession autour du champ effectif dans le sens des aiguilles d’une montre, conformément à l’équation LLG. En présence de l’amortissement de Gilbert (le terme avec \alpha), l’énergie cinétique du système est finalement dissipée et le macrospin retrouve son énergie minimale, c’est-à-dire qu’il s’aligne sur le champ effectif. Cette dynamique de précession est liée à la résonance ferromagnétique (FMR), où la fréquence angulaire dépend linéairement de l’intensité du champ appliqué.

Les ondes de spin apparaissent lorsqu’on introduit des interactions non locales, par exemple des interactions d’échange à courte portée qui prennent la forme H_{\rm{eff}}=A \triangledown^2\textbf{m} dans la limite continue avec A le coefficient de rigidité d’échange. En présence d’une interaction d’échange, le mode de précession d’un seul macrospin peut se propager aux macrospins voisins, entraînant un courant de moment cinétique qui se propage, e.g. les ondes de spin.

Les ondes électromagnétiques et élastiques peuvent être confinées ou dirigées grâce à une nanostructure, tout comme les ondes de spin. De plus, les ondes de spin peuvent être manipulées par des textures magnétiques, c’est-à-dire la distribution non homogène de l’ordre de magnétisation. Un exemple est la paroi de domaine magnétique, la zone de transition entre deux domaines magnétiques avec une magnétisation opposée. Il a été démontré, tant sur le plan théorique qu’expérimental, que la paroi de domaine peut servir de canal conducteur pour les ondes de spin, ce qui peut être utilisé pour concevoir des circuits à ondes de spin reconfigurables.

Les simulations micromagnétiques peuvent contribuer à expliquer des découvertes expérimentales. Il existe également de nombreux exemples de succès dans lesquels la simulation micromagnétique a permis de prédire de nouveaux phénomènes qui ont ensuite été vérifiés par des expériences.

Le module Micromagnetics développé avec le Constructeur de physique

Il existe deux logiciels open source populaires de simulation micromagnétique : Object Oriented MicroMagnetic Framework (OOMMF) etMumax, accéléré par GPU³.

Nous préférons effectuer la simulation micromagnétique à l’aide de COMSOL Multiphysics^® pour deux raisons :

1. COMSOL Multiphysics^® est basé sur la méthode des éléments finis plutôt que sur la méthode des différences finies utilisée par OOMMF et Mumax³. La méthode des éléments finis s’avère plus performante pour la modélisation de géométries et de structures complexes.
2. Le module Micromagnetics peut être utilisé directement avec de nombreux modules physiques de COMSOL Multiphysics^®. En combinant par exemple le module AC/DC (courants électriques et champs électromagnétiques) et le module RF (micro-ondes), il est possible de modéliser l’interaction dipolaire dans un aimant. En combinant le module construit sur mesure avec le module Structural Mechanics, il est possible de modéliser les effets magnéto-élastiques, tandis que le module Heat Transfer peut être utilisé pour modéliser les effets thermiques dans un aimant. Les couplages multiphysiques entre la physique personnalisée et les produits complémentaires deviennent très simples à réaliser dans ce cadre.

Les utilisateurs intéressés par l’utilisation du module Micromagnetics avec COMSOL Multiphysics^® peuvent installer le fichier compilé du module, Micromagnetics Module.jar, dans les archives COMSOL locales. Une nouvelle interface physique, Micromagnétique (mm), apparaît lors de la sélection de la physique.

Le Module Micromagnétique (V1.33) présente l’interface utilisateur illustrée ci-dessous.

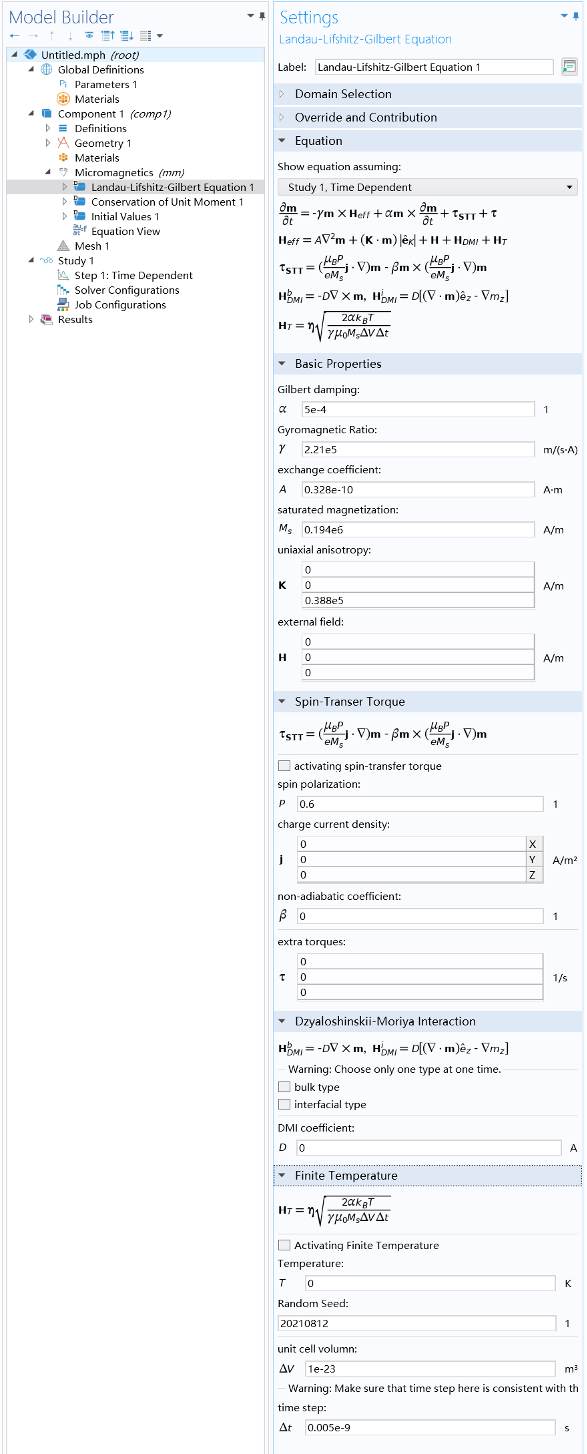
Le module Micromagnetics (V1.33) dispose de presque toutes les fonctionnalités proposées par d’autres logiciels open source, notamment mais pas seulement :

• Formalisme basique de Landau-Lifshitz-Gilbert, incluant les interactions d’échange et l’anisotropie uniaxiale
• Interaction Dzyaloshinskii-Moriya (de types bulk et interfacial) avec conditions aux limites appropriées
• Couple de transfert de spin avec termes d’amortissement et de champ
• Entrée arbitraire de champ et de couple (fonction du temps et de l’espace)
• Effet de température finie (avec graine aléatoire arbitraire)
• Conditions aux limites fixes et conditions aux limites périodiques
• Capacité à résoudre plusieurs équations LLG indépendantes dans une région (telles que les antiferromagnétiques synthétiques ayant plusieurs sous-réseaux)
• Capacité de couplage multiphysique comprenant les couplages magnéto-dipolaire, magnéto-élastique, magnéto-électrique et magnéto-thermique

Grâce au module Micromagnetics, nous avons démontré de nombreux phénomènes physiques intéressants liés aux ondes de spin et proposé divers dispositifs à ondes de spin, tels que la diode à ondes de spin (Réf. 5), la fibre à ondes de spin (Réf. 6), le polariseur et le retardateur à ondes de spin (Réfs. 7-8), ainsi que les grilles logiques magnétiques (Réf. 9).

Couplages multiphysiques avec le module Micromagnetics

Comme mentionné ci-dessus, l’un des avantages de COMSOL Multiphysics^® est sa capacité à réaliser des couplages multiphysiques entre les fonctionnalités de ses modules complémentaires. Les ondes de spin peuvent être manipulées par des champs magnétiques, des déformations de réseau, des gradients de température, etc. Les systèmes couplant des ondes de spin et d’autres excitations (telles que des ondes électromagnétiques et élastiques) peuvent combiner les avantages des deux mondes et produire une physique riche, facilitant la génération et la transmission d’informations. Nous allons maintenant montrer les couplages multiphysiques qui peuvent être réalisés à l’aide du module Micromagnetics.

La magnonique des cavités (Réf. 10) est une science interdisciplinaire qui combine la magnonique et l’électrodynamique quantique en cavité (CQED). L’une des applications de la CQED consiste à réaliser le traitement de l’information quantique en manipulant l’interaction entre les photons et la matière. Une configuration typique en magnonique des cavités consiste en une cavité micro-ondes dans laquelle sont placés des aimants. Les aimants sont couplés aux ondes électromagnétiques stationnaires ou se propageant dans la cavité. De tels systèmes offrent une nouvelle option pour étudier la manipulation du courant de spin et la dynamique non linéaire des moments magnétiques (Réfs. 11-12). Le système de cavité magnonique peut être simulé en couplant le module Micromagnetics et le module RF. Pour la simulation magnétostatique, le couplage entre le module Micromagnetics et le module AC/DC (champs magnétiques) est suffisant.

La mécanique des spins inclut l’interaction entre la magnétisation et la déformation du réseau cristallin. Dans les matériaux présentant un couplage magnéto-élastique (ou une magnétostriction), les variations spatiales et temporelles de la magnétisation (ondes de spin) exercent des forces sur le réseau cristallin, et le réseau déformé (ondes élastiques) produit des champs qui agissent en retour sur la magnétisation. Ainsi, comme le montre l’animation ci-dessous, un disque magnétisé est excité par des champs magnétiques, et la magnétisation précessive rayonne des ondes élastiques vers le substrat. Le problème de mécanique des spins peut être simulé en couplant le module Micromagnetics et le module Structural Mechanics.

Textures auto-adaptatives avec courant électrique

Dans les aimants métalliques, les courants électriques polarisés en spin exercent un couple de transfert de spin sur les moments magnétiques locaux, provoquant un mouvement de texture dû au courant. Étant donné que la conductivité au sein du film magnétique dépend de l’orientation relative de la magnétisation locale et de la direction du courant en raison de la magnétorésistance anisotrope (AMR), l’interaction entre le courant, le couple et la texture peut être modélisée à l’aide du module Micromagnetics et du module AC/DC (courants électriques).

Comme le montre l’animation ci-dessous, les tensions appliquées sur deux électrodes modifient les textures magnétiques (en haut) via un couple de transfert de spin. La conductivité locale et la distribution de la densité de courant (en bas) changent en conséquence. Les textures magnétiques s’adaptent finalement à une configuration stable, ce qui entraîne une augmentation de la conductance entre les deux électrodes. Il est suggéré qu’un tel comportement de rétroaction positive puisse être utilisé pour le calcul neuromorphique (Réf. 13).

Comment accéder au module Micromagnetics

Les fichiers du module Micromagnetics sont distribués gratuitement via la pageÉchange de modèles COMSOL. Le package téléchargé comprend le fichier d’installation du module et un guide d’utilisation contenant des instructions d’installation et des exemples. Nous apprécions toutes les suggestions, rapports et communications des utilisateurs. D’autres fonctionnalités seront activement mises à jour dans les versions futures.

Pour vous aider à apprendre à utiliser le module, vous pouvez également accéder à des modèles exemples mis à jour par l’auteur et son équipe via l’entrée suivante de la page Échange de modèles : Tutorial Examples for Micromagnetic Module.

Remerciements

L’auteur remercie le professeur Jiang Xiao de l’université Fudan pour sa supervision et l’Institut des dispositifs nanoélectroniques et de l’informatique quantique de l’université Fudan pour son soutien.

À propos de l’auteur

Le Dr Weichao Yu est titulaire d’une licence en physique appliquée de la Faculté des sciences physiques et de l’ingénierie de l’Université Tongji (Chine) et d’un doctorat en physique théorique de l’Université Fudan (Chine). Il a travaillé comme chercheur postdoctoral à l’Université Fudan et comme professeur assistant à l’Institut de recherche sur les matériaux de l’Université Tohoku (Japon). Il est actuellement chercheur à l’Institut des dispositifs nanoélectroniques et de l’informatique quantique de l’Université Fudan. Les recherches du Dr Yu portent sur les phénomènes fondamentaux en spintronique et en magnétisme, notamment la dynamique des textures magnétiques et des ondes de spin ainsi que le couplage entre les systèmes magnétiques et d’autres systèmes multiphysiques, tels que la cavitronique de spin ou la spintronique de cavité (couplage entre magnons et photons) et la mécanique de spin (couplage entre ondes de spin et ondes élastiques). Il propose et conçoit de nouveaux types de dispositifs spintroniques et de nouveaux concepts pour l’informatique non conventionnelle, tels que l’informatique logique en mémoire basée sur des systèmes magnétiques et l’informatique neuromorphique avec des fonctionnalités d’auto-apprentissage. Il a également développé un module de simulation micromagnétique basé sur la méthode des éléments finis, capable de s’interfacer de manière bidirectionnelle avec d’autres systèmes multiphysiques, facilitant ainsi l’étude du magnétisme fondamental et la conception de nouveaux dispositifs spintroniques.

Références

1. A. Barman et al., The 2021 Magnonics Roadmap, J. Phys.: Condens. Matter, vol. 33, no. 413001, 2021.
2. A. V. Chumak et al., Magnon Spintronics, Nature Physics, vol. 11, no. 453, 2015.
3. H. Yu, J. Xiao, and H. Schultheiss, Magnetic Texture Based Magnonics, Physics Reports, vol. 905, no. 1, 2021.
4. V. G. Bar’yakhtar and B. A. Ivanov, The Landau-Lifshitz Equation: 80 Years of History, Advances, and Prospects, Low Temperature Physics, vol. 41, no. 663, 2015.
5. J. Lan, W. Yu, R. Wu, and J. Xiao, Spin-Wave Diode, Phys. Rev. X, vol. 5, no. 041049, 2015.
6. W. Yu, J. Lan, R. Wu, and J. Xiao, Magnetic Snell’s Law and Spin-Wave Fiber with Dzyaloshinskii-Moriya Interaction, Phys. Rev. B, vol. 94, no. 140410, 2016.
7. J. Lan, W. Yu, and J. Xiao, Antiferromagnetic Domain Wall as Spin Wave Polarizer and Retarder, Nature Communications, vol. 8, no. 178, 2017.
8. W. Yu, J. Lan, and J. Xiao, Polarization-Selective Spin Wave Driven Domain-Wall Motion in Antiferromagnets, Phys. Rev. B, vol. 98, no. 144422, 2018.
9. W. Yu, J. Lan, and J. Xiao, Magnetic Logic Gate Based on Polarized Spin Waves, Phys. Rev. Applied, vol. 13, no. 024055, 2020.
10. B. Z. Rameshti, S. V. Kusminskiy, J. A. Haigh, K. Usami, D. Lachance-Quirion, Y. Nakamura, C.-M. Hu, H. X. Tang, G. E. W. Bauer, and Y. M. Blanter, Cavity Magnonics, ArXiv:2106.09312 [Cond-Mat], 2021.
11. W. Yu, J. Wang, H. Y. Yuan, and J. Xiao, Prediction of Attractive Level Crossing via a Dissipative Mode, Phys. Rev. Lett., vol. 123, no. 227201, 2019.
12. W. Yu, T. Yu, and G. E. W. Bauer, Circulating Cavity Magnon Polaritons, Phys. Rev. B, vol. 102, no. 064416, 2020.
13. W. Yu, J. Xiao, and G. E. W. Bauer, A Hopfield Neural Network in Magnetic Films with Natural Learning, ArXiv:2101.03016 [Cond-Mat], 2021.