Frontières d’absorption du son : Réaction locale ou étendue

Aujourd’hui, l’étude par la simulation numérique de l’acoustique des salles ou de l’acoustique architecturale est un élément essentiel de la conception d’un son de qualité, qu’il s’agisse de créer une scène virtuelle immersive, de concevoir un environnement acoustique confortable dans une salle ou d’optimiser une expérience audio. Le module Acoustics, un add-on du logiciel COMSOL Multiphysics^®, comprend plusieurs interfaces qui conviennent particulièrement pour la simulation de l’acoustique des salles. Cet article de blog se concentre sur l’importance des conditions limites d’absorption du son pour la modélisation de l’acoustique des salles.

Performance d’absorption du son

Pour comprendre la condition limite d’absorption acoustique, nous allons d’abord nous intéresser au coefficient d’absorption acoustique. Pour exprimer les caractéristiques d’absorption des absorbeurs, les trois grandeurs suivantes sont utilisées (Réf. 1) :

• Coefficient d’absorption sonore, \alpha: le rapport entre l’énergie sonore non réfléchie et l’énergie sonore incidente
• Impédance acoustique spécifique, Z_{\rm n}: le rapport entre la pression acoustique et la vitesse normale des particules à la surface de l’absorbeur acoustique
• Coefficient à valeur complexe de réflexion de la pression, R: le rapport entre la pression acoustique réfléchie et la pression acoustique incidente

Analysons maintenant ces paramètres dans la situation idéale décrite ci-dessous, où l’onde plane pénètre dans l’absorbeur poreux.

Onde plane incidente arrivant sur le matériau poreux.

Ici, les nombres d’ondes de l’air et du matériau poreux sont notés respectivement k et k_{\rm e}. Les pressions acoustiques incidente, réfléchie et transmise sont notées p_{\rm i}, p_{\rm r}, et p_{\rm t}. Les angles d’incidence, de réflexion et de transmission sont notés \theta, \psi, et \phi. Les amplitudes des ondes sonores incidentes et réfléchies sont représentées par A_{\rm i} et A_{\rm r}B_{\rm t} et B_{\rm b}. L’absorbeur poreux d’une épaisseur de d m a été considéré comme le fluide équivalent (voir notre Page Cyclopedia) pour plus d’informations. La terminaison avec une frontière rigide a été fixée à x=d.

D’après l’équation linéaire des ondes acoustiques, la vitesse des particules dans la direction x du son incident, du son réfléchi et du son transmis sont respectivement v_{\rm i}, v_{\rm r}, et v_{\rm t} et peuvent être exprimées comme suit :

Ici, Z_{\rm 0} et Z_{\rm C} représentent l’impédance caractéristique de l’air et du matériau poreux. Par définition, le coefficient de réflexion s’écrit :

À l’interface entre l’air et la couche poreuse (x=0), les deux conditions de continuité suivantes sont posées :

Avec ces conditions de continuité et le principe de Fermat, \theta=\phi, l’impédance acoustique spécifique peut être exprimée comme suit :

Ainsi,

Le coefficient d’absorption peut être déterminé à l’aide de l’équation suivante:

Ainsi, vous pouvez modéliser l’absorption du son sur les frontières en attribuant l’une des trois quantités aux frontières. L’équation ci-dessus montre également que \alpha dépend intrinsèquement de l’angle d’incidence. On note que R et Z_{\rm n} sont des paramètres à valeurs complexes qui contiennent des informations sur la phase, tandis que \alpha est un paramètre lié à l’énergie. L’information sur la phase étant importante afin de simuler avec précision les modes de la pièce, les paramètres complexes sont généralement de meilleures données d’entrée pour les simulations d’acoustique des salles avec une approche ondulatoire. D’autre part, le coefficient d’absorption acoustique permet d’interpréter intuitivement les performances de l’absorbeur et constitue le principal résultat pour un essai d’absorption acoustique. Le coefficient aléatoire d’absorption incidente, qui est la valeur moyenne pour les angles solides, caractérise en pratique la performance des absorbeurs.

Dans les équations suivantes, nous étudions plus en détail l’impédance acoustique du matériau poreux.

La pression de transmission et la vitesse à x=0 sont les suivantes :

D’autre part, celles à x=d sont les suivantes :

Avec ces équations, nous pouvons exprimer les paramètres à l’entrée avec des valeurs terminales en utilisant la forme matricielle suivante:

Ici, {\bm T}_{\rm F} correspond à la matrice de transfert de la couche fluide, qui a été largement utilisée pour modéliser l’absorption et l’isolation acoustique à l’aide de la méthode des matrices de transfert (TMM) (Réf. 2). En utilisant la Loi de Snell indiquant que ksin\theta = k_{\rm e}\sin\phi, nous pouvons réécrire {\bm T}_{\rm F} de la façon suivante:

avec k_{\rm n}=(k_{\rm e}^2-k^2\sin^2{\theta})^{\frac{1}{2}}. Sous la condition aux limites de rigidité au niveau du terminal (v_{\rm t}(d) = 0), nous pouvons calculer l’impédance acoustique spécifique de l’absorbeur poreux comme suit:

L’équation ci-dessus indique que l’impédance acoustique spécifique dépend elle-même de l’angle. Ainsi, pour modéliser complètement l’absorption acoustique au niveau d’une frontière, il est nécessaire de prendre en compte la dépendance angulaire de l’absorbeur.

Modèles de réaction locale et étendue

Lors de la modélisation de l’absorption acoustique aux frontières, deux types de modèles peuvent être adoptés — les modèles de réaction locale et étendue. Le modèle de réaction locale, un standard dans la simulation de l’acoustique des salles, utilise une impédance indépendante de l’angle pour décrire la propriété d’absorption du son au niveau de la frontière (généralement la valeur d’impédance de la condition d’incidence normale). Avec cette approche, on suppose que la vitesse des particules en un point donné de la surface de l’absorbeur est indépendante du comportement en d’autres points de la surface. À l’inverse, le modèle de réaction étendue adapte l’impédance et la rend dépendante de l’angle. Il est évident que le modèle de réaction locale est approximatif, mais il est efficace et fonctionne bien pour modéliser les absorbeurs acoustiques dont l’impédance acoustique dépend peu de l’angle, tels que les matériaux poreux à structure rigide avec une résistivité à l’écoulement élevée et les absorbeurs à âme en nid d’abeille. D’un autre côté, le modèle de réaction étendue est précis, mais il nécessite généralement une modélisation supplémentaire de l’intérieur de l’absorbeur. Pour obtenir une modélisation acoustique précise et efficace de la salle considérée, il est nécessaire de choisir un modèle de limite d’absorption approprié pour l’absorbeur utilisé. Dans la section suivante, l’effet du type de frontière d’absorption sur le coefficient aléatoire d’absorption incidente est illustré théoriquement et numériquement.

Comment les différents modèles de surface affectent les performances d’absorption

Dans cette partie, il s’agit d’évaluer les performances d’absorption d’un absorbeur poreux à structure rigide et d’un rideau acoustique avec une couche d’air arrière. Le matériau poreux est considéré comme un fluide équivalent avec une épaisseur de 100 mm. La propriété du fluide est modélisée à l’aide du modèle empirique de Miki pour une résistivité à l’écoulement de 13 900 Pa*s/m². Le rideau acoustique utilisé étant très fin par rapport à la longueur d’onde aux fréquences étudiées, le modèle de membrane perméable est utilisé puis couplé à la couche d’air. Avec le modèle de membrane perméable, l’impédance de transfert du rideau est calculée avec l’équation suivante:

Ici, R_{\rm C} et M_{\rm C} représentent la résistance à l’écoulement et la densité de surface, et sont respectivement fixées à 416 Pa*s/m et 0.5 kg/m² . Pour l’étude théorique, le TMM est utilisé et le coefficient d’absorption statistique est évalué comme la valeur d’incidence aléatoire. La définition du coefficient d’absorption statistique \alpha_{\rm s} est présentée ci-dessous:

La matrice de transfert {\bm T}_{\rm T} d’un matériau mince est exprimée comme suit:

L’équation ci-dessus décrivant la matrice de transfert permet d’écrire l’impédance acoustique spécifique du rideau acoustique avec couche d’air de la façon suivante:

Pour le TMM, le modèle de réaction locale peut être évalué en utilisant \theta=0.

Dans l’étude numérique, nous calculons le coefficient d’absorption de la salle de réverbération, qui est le coefficient d’absorption mesuré dans la salle de réverbération. La valeur du coefficient dépend de la taille de la salle mesurée et de la taille de l’échantillon. Le coefficient d’absorption a été normalisé en tant que procédure de mesure dès la norme ISO:354, et est largement utilisé dans la conception acoustique des salles.

L’unique sol dur avec absorbeur acoustique intégré a été modélisé en deux dimensions, afin de simuler efficacement la mesure du coefficient d’absorption de la salle de réverbération avec COMSOL Multiphysics^®. Cela est illustré dans l’image ci-dessous:

Modèle d’absorbeur acoustique intégré pour l’évaluation du coefficient d’absorption de la salle de réverbération.

L’étude de vérification de la Réf. 3 a montré que ce modèle simplifié permettait d’approcher étroitement la mesure du coefficient de réverbération.

L’interface Pression acoustique, éléments de frontière a été utilisée pour modéliser le champ de pression incident et le plancher rigide, et l’interface Pression acoustique, domaine fréquentiel a été utilisée pour modéliser la pression à l’intérieur de l’absorbeur. La fonctionnalité Poroacoustique a été appliquée au matériau poreux. Avec le noeud multiphysique Frontière entre modèles acoustiques BEM–FEM, l’impédance de transfert du rideau acoustique peut être définie simultanément. Pour la modélisation de la réaction locale, le domaine de l’absorbeur est désactivé et l’impédance acoustique incidente normale correspondante est attribuée à la surface de l’absorbeur. L’évaluation du coefficient d’absorption de la salle de réverbération s’effectue selon les étapes suivantes:

1. Evaluer l’énergie incidente W_{{\rm i},\theta_n} et l’énergie absorbée W_{{\rm a},\theta_n} sur la surface de l’absorbeur pour une onde plane ayant un angle d’incidence de \theta_n.
2. Calcul du rapport entre l’énergie totale absorbée et l’énergie totale incidente à l’aide de l’équation suivante.

Le coefficient d’absorption de la salle de réverbération \alpha_{\rm r} est exprimé ci-dessous.

Ici, N représente le nombre d’angles d’incidence. Dans le test numérique, le champ incident de l’onde plane a été modélisé avec la fonctionnalité Champ de pression ambiante, et W_{{\rm i},\theta_n} et W_{{\rm a},\theta_n} ont été définis comme suit:

où p_0 est une amplitude de la pression incidente, et \bm n et {\bm I}_{\theta_n} sont respectivement le vecteur normal et le vecteur d’intensité sonore de l’angle d’incidence {\theta_n} sur la surface de l’absorbeur.

Le graphique ci-dessous compare les coefficients aléatoires d’absorption incidente de l’absorbeur poreux. La différence entre le modèle de réaction locale et le modèle de réaction étendue est faible, mais elle est visible, en particulier à hautes fréquences. Ainsi, comme illustré ci-dessus, le modèle de réaction locale semble être une bonne approximation pour le matériau poreux avec une résistivité à l’écoulement élevée et une extrémité rigide.

Coefficients aléatoires d’absorption incidente de l’absorbeur poreux.

D’autre part, la comparaison des coefficients aléatoires d’absorption incidente du rideau acoustique, illustrée ci-dessous, présente un écart important entre le modèle de réaction locale et le modèle de réaction étendue. Cela est dû à la forte dépendance de la couche d’air par rapport à l’angle d’incidence. Ces résultats permettent de mettre en lumière la règle conventionnelle selon laquelle la modélisation de la réaction étendue est primordiale pour modéliser précisément les absorbeurs avec couche d’air.

Coefficients aléatoires d’absorption incidente du rideau acoustique.

Coefficients d’absorption des salles réverbérantes vs. valeurs statistiques ?

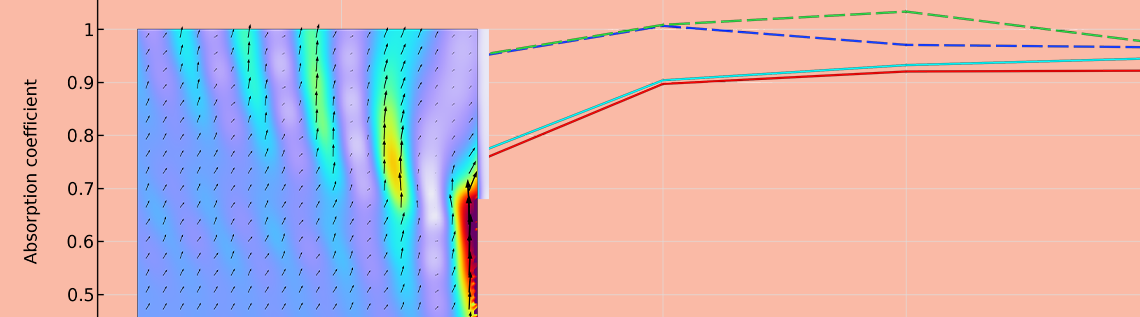
Comme le montrent les graphiques des coefficients d’absorption ci-dessus, quels que soient le type d’absorbeurs et les modèles d’absorption aux frontières, les coefficients d’absorption de la salle de réverbération sont supérieurs aux valeurs statistiques et dépassent même la valeur de 1 (une absorption parfaite). Ce phénomène, appelé « effet de bord », est typique des mesures expérimentales et est causé par le flux d’énergie qui se dirige du sol rigide vers la surface de l’absorbeur. Une telle situation est illustrée par le modèle de réaction étendue du rideau acoustique ci-dessous pour un angle d’incidence de 60^° à 500 Hz. Le flux d’énergie est causé par le gradient de pression acoustique autour du bord de l’échantillon: la pression acoustique près du sol prend une valeur plus importante en raison de la contribution du son réfléchi, tandis que la pression acoustique devant l’absorbeur devient plus faible en raison de l’effet d’absorption du son. Le flux d’énergie se produit autour du bord de l’échantillon, et son effet sur le coefficient d’absorption acoustique peut être réduit en augmentant la surface de l’échantillon. Par conséquent, la taille de l’échantillon pour mesurer le coefficient d’absorption de la salle de réverbération est réglementée par la norme ISO:354.

Visualisation de l’amplitude acoustique et des flèches d’intensité acoustique à 500 Hz pour un angle d’incidence de 60^°.

Conclusion

Cet article de blog présente d’un point de vue théorique l’absorption acoustique aux frontières et étudie comment le type de modèle choisi affecte les performances en terme d’absorption acoustique. Pour la modélisation de l’acoustique des salles ou de l’acoustique architecturale, les interfaces Lancer de rayons acoustique, Pression acoustique, domaine fréquentiel et Pression acoustique, explicite en temps sont des interfaces physiques bien adaptées avec COMSOL^®. En parallèle, l’interface Lancer de rayons acoustique est basée sur l’acoustique géométrique et ne peut pas capturer avec précision le comportement des ondes acoustiques. Cependant, cette implémentation peut caractériser le comportement de l’absorption acoustique sur les surfaces en fonction de l’angle d’incidence, ce qui permet d’améliorer la précision de la modélisation de l’acoustique des salles.

Les approches basées sur les ondes permettent de modéliser avec exactitude les caractéristiques d’absorption du son aux frontières. Les fonctionnalités Poroacoustique et Impédance intérieure sont en particulier utilisées pour modéliser la réactivité étendue des frontières absorbantes. L’interface Pression acoustique, domaine fréquentiel peut facilement traiter ces conditions car la méthode est intrinsèquement dépendante de la fréquence. D’autre part, la modélisation dans le domaine temporel des conditions aux limites de réaction étendue est ardue, en raison de la difficulté à modéliser la dépendance en fréquence de la propriété d’absorption dans le domaine temporel. Cependant, nous pouvons utiliser la fonctionnalité Poroacoustique dans le domaine temporel pour modéliser des absorbeurs poreux avec une réactivité étendue. La version temporelle de cette fonctionnalité utilise une méthode d’équation différentielle auxiliaire efficace pour tenir compte de la dépendance en fréquence des matériaux poreux. Ainsi, vous pouvez choisir avec souplesse les modèles de limites d’absorption du son en fonction de la configuration des absorbeurs.

Dans un futur article de blog, nous utiliserons la fonctionnalité Poroacoustique dans le domaine temporel pour explorer et discuter de la manière dont le choix des types des cloisons insonorisantes affecte l’acoustique d’une salle de réunion.

Références

1. Z. Maekawa, J. H. Rindel and P. Lord. Environmental and Architectural Acoustics. CRC Press, 2010.
2. J.F. Allard and N. Atalla. Propagation of Sound in Porous Media: Modelling Sound Absorbing Materials. Wiley, 2009.
3. T. Sakuma, S, Sakamoto and T. Otsuru. Computational Simulation in Architectural and Environmental Acoustics: Methods and Applications of Wave-Based Computation. Springer, 2014.