
Explorer la fonctionnalité d’ajustement par fractions partielles dans COMSOL Multiphysics®
Aujourd’hui, notre invité en tant que bloggueur René Christensen d’Acculution ApS parle de la fonctionnalité Ajustement par fractions partielles, introduite dans la version 6.2 du logiciel COMSOL Multiphysics®.
La version 6.2 du logiciel COMSOL Multiphysics®, comporte une nouvelle fonction Ajustement par fractions partielles. Cette fonctionnalité analyse une fonction de fréquence à valeurs complexes donnée par ses parties réelle et imaginaire. Il en résulte une somme de plusieurs fractions qui correspondent à la fonction et qui décrivent le système de manière très compacte dans la gamme de fréquence en question. Les fractions sont connues sous le nom de fractions partielles qui, ensemble, constituent une fonction de transfert numérique, ce qui permet de mieux comprendre le fonctionnement interne du système sous-jacent et facilite la transformation dans le domaine temporel. Les parties réelles et imaginaires des valeurs d’entrée proviennent généralement de simulations préliminaires, mais il peut également s’agir de valeurs importées d’autres logiciels ou même d’autres mesures.
Table des matières
- Transformation temporel vers fréquentiel
- Fonctions de transfert
- Décomposition en fractions partielles
- Ajustement par fractions partielles
- Pôles réels
- Pôles complexes
- Pôles répétitifs
- Pôles instables
- Fonction de transfert irrationnelle: retard temporel
- Fonction de transfert irrationnelle : Microacoustique
- Symétrie conjuguée, fréquences négatives
- Conclusion
Transformation temporel vers fréquentiel
Puisque la fonctionnalité implique une analyse en domaine fréquentiel, il est intéressant d’examiner brièvement certains aspects du fonctionnement en domaine fréquentiel et la démarche à suivre pour les signaux et les systèmes.
Bien que les signaux varient généralement dans le temps, il est souvent plus facile de les analyser dans le domaine fréquentiel. De même, les systèmes sont le plus souvent analysés en convertissant certains aspects de leurs caractéristiques temporelles en caractéristiques fréquentielles. La conversion entre le domaine temporel et le domaine fréquentiel s’effectue généralement par le biais de la transformée de Fourier ou de Laplace et de leurs transformées inverses respectives. Bien qu’il y ait un recoupement important entre les deux, nous nous concentrerons ici sur la transformée de Laplace, qui est traditionnellement utilisée pour l’analyse des systèmes. La transformée de Laplace est donnée par l’intégrale unilatérale:
où s est une fréquence complexe définie par la fréquence angulaire, \omega, et l’amortissement, \sigma, telle que
Cette unilatéralité rend cette intégrale adaptée aux systèmes, car ils peuvent alors disposer d’un temps spécifique auquel ils sont « allumés », et le comportement transitoire peut donc être étudié. En outre, la transformée de Laplace servira de transformée principale pour établir les fonctions de transfert dont il sera question plus loin. Quelques paires temps–fréquence importantes sont énumérées dans le tableau ci-dessous:
| f(t) | F(s) |
|---|---|
| kf^{(n)}(t) | s k F(s) + k f(0) |
| k \int^{t}_0 f(\tau) d\tau | k\frac{F(s)}{s} |
| t^n e^{-\sigma_0 t} | \frac{n!}{(s+\sigma_0)^{n+1}} |
| ke^{-\sigma_0t}\cos(\omega_0t) | k \frac{s + \sigma_0}{(s + \sigma_0)^2 + \omega^2_0} |
| ke^{-\sigma_0t}\sin(\omega_0t) | k \frac{\omega_0}{(s+\sigma_0)^2 + \omega^2_0} |
Fonctions de transfert
De nombreux systèmes peuvent être décrits par des équations différentielles linéaires à coefficients constants et réels, formant ce que l’on appelle des systèmes réels linéaires invariants dans le temps (LTI). Un exemple pourrait être un système masse–ressort–amortisseur avec une vitesse (sortie), v, pour une force externe (entrée), f_\textrm{ext}, tel que:
où m est la masse, r est la résistance, et k est la rigidité. Ici, nous écrivons en termes de vitesse plutôt que de déplacement ou d’accélération car la force et la vitesse sont des variables conjuguées dont le produit est une puissance, tout comme le sont la tension et l’intensité du courant dans les systèmes électriques.
La transformée de Laplace est ensuite effectuée en supposant qu’en régime permanent, les phaseurs d’entrée et de sortie, possiblement amortis, sont de la forme exponentielle complexe F(s) = (F_0e^{\phi_F(s)})e^{st} et V(s) = (V_0e^{\phi_V(s)})e^{st}, respectivement, où F_0 et V_0 sont des nombres réels. Ces hypothèses conduisent à la description du système dans le domaine fréquentiel:
Les conditions initiales sont ici ignorées, mais elles peuvent également être incluses dans l’équation ci-dessus. Étant donné que nous sommes souvent intéressés par la sortie résultante, Y(s), pour une entrée, X(s), nous pouvons utiliser une fonction de transfert générale:
Pour le système actuel, on obtient la fonction de transfert:
En dynamique, il est très courant que la fonction de transfert associée à un système LTI soit une fonction rationnelle, correspondant à une fraction de deux polynômes univariés qui impliquent uniquement la variable s telle que:
On peut aussi l’écrire sous une forme factorisée par rapport aux zéros et aux pôles, comme suit :
où
Un aspect notable des fonctions de transfert rationnelles est leur ordre, qui est le degré le plus élevé de s dans le dénominateur ci-dessus, donné directement par l’exposant n. Un autre aspect notable est leur propriété. Il y a trois catégories à considérer. L’une est dite propre, pour laquelle l’ordre du dénominateur est supérieur ou égal à l’ordre du numérateur; c’est-à-dire, n \geq m. Une autre catégorie, étant un sous-ensemble, est appellée strictement propre, pour laquelle le nombre de pôles est (strictement) supérieur au nombre de zéros; c’est-à-dire, n > m. Enfin, la troisième catégorie est celle des impropres, pour laquelle n < m. Dans le dernier cas, vous devez tenir compte des problèmes potentiels de stabilité et de causalité, mais la propriété est également affectée par le fait que l’analyse soit effectuée pour une fonction de transfert particulière ou pour son inverse.
Pour un système masse–ressort–amortisseur, la fonction de transfert entre dans la catégorie des filtres passe-bande, ce qui est logique, puisqu’à une fréquence particulière il y aura une résonance de la vitesse pour la force appliquée. La forme standard d’une fonction passe-bande étant
nous pouvons trouver la fréquence angulaire caractéristique:
et
L’ordre du système masse–ressort–amortisseur est de deux. Cela signifie également qu’il y a deux racines associées au polynôme du dénominateur: les pôles. Pour les systèmes réels considérés ici, il existe trois possibilités pour les deux pôles: 1) deux pôles réels distincts, 2) deux pôles réels qui se chevauchent (se répètent), ou 3) deux pôles complexes conjugués. Les racines du numérateur sont appelées zéros, et les zéros et les pôles décriront entièrement les systèmes linéaires qui nous intéressent avec des coefficients réels invariants dans le temps, à condition que la région de convergence (ROC) soit connue. Ici, nous supposons des systèmes causaux, et la ROC sera donc connue grâce à cette information. Cela conduira à des systèmes stables n’ayant pas de pôles dans le demi-plan droit du plan complexe s. Cela garantira également l’existence d’une transformée de Fourier, nécessaire pour justifier la recherche d’une réponse en fréquence à partir de la fonction de transfert. Les systèmes étant réels, il existe une symétrie conjuguée et, comme nous l’avons déjà mentionné, les pôles complexes se présenteront toujours par paires conjuguées.
Décomposition en fractions partielles
Quand on étudie les fonctions de transfert et les transformées de Fourier/Laplace (inverses), il arrive que l’on aborde le sujet de la décomposition en fractions partielles (DFP). Ici, l’objectif est généralement de faciliter la recherche des transformées de Laplace inverses à l’aide de tables. Les fonctions de transfert d’ordre supérieur peuvent être décomposées en fractions plus simples, et leurs transformées inverses s’additionneront pour former l’inverse total puisque la linéarité s’applique aux systèmes en question. Cela peut également s’avérer utile lors de la résolution d’intégrales de fonctions rationnelles. Enfin, en théorie du contrôle il peut être intéressant de décomposer une fonction de transfert d’ordre supérieur en plusieurs fractions d’ordre inférieur.
Nous allons maintenant illustrer la procédure de décomposition d’une fonction de transfert en ses fractions partielles, lorsque les pôles peuvent être écrits sous une forme factorisée. La fonction de transfert est d’ordre 5, avec un pôle double répétitif de -5 et un pôle triple répétitif de 0. Nous aurons donc besoin de 5 fractions partielles:
En multipliant par le dénominateur, on obtient:
En comparant les différents ordres des membres du côté gauche et du côté droit, les inconnues peuvent être trouvées comme suit A=0.52, B = -1.6, C=4, D=-0.52, et E=-1.
En utilisant les tables de la transformée de Laplace inverse, on peut trouver la réponse impulsionnelle du système associé comme suit:
L’exécution de cette transformation inverse directement à partir de la fonction de transfert originale nécessiterait l’utilisation d’un logiciel de calcul mathématique, mais avec la décomposition en fractions partielles, il est possible de l’effectuer analytiquement à la main, du moins lorsque les zéros et les pôles sont connus numériquement. Notez que pour les fonctions de transfert impropres, il peut être nécessaire d’effectuer une division longue polynomiale pour diviser la fonction de transfert initiale en une valeur asymptotique et en fractions résultantes.
La relation temps-fréquence est mise à profit avec la nouvelle possibilité d’avoir une impédance dépendante de la fréquence dans l’acoustique en domaine temporel, en utilisant la fonction Ajustement par fractions partielles (PFF).
Ajustement par fractions partielles
Bien qu’il ne soit généralement pas possible de trouver une fonction de transfert analytique pour un problème multiphysique simulé, il est toujours possible de trouver un rapport entre une sortie et une entrée sous la forme de valeurs complexes tabulées. Ces valeurs peuvent être le résultat d’une simulation ou, alternativement, des valeurs importées de mesures expérimentales. S’il existait un moyen d’établir une fonction de transfert à partir des valeurs tabulées, on pourrait obtenir des informations sur le système qui seraient difficiles à discerner directement à partir des valeurs seulement. Il serait alors également possible d’effectuer une transformée de Fourier inverse analytique pour former la réponse impulsionnelle, au lieu de devoir effectuer, par exemple, une étude de transformée de Fourier rapide inverse. Enfin, la description du système en termes de zéros et de pôles au lieu d’un grand tableau de données réduit la taille du système, tout en conservant toutes ses caractéristiques, au moins dans la gamme de fréquences choisie pour les valeurs tabulées. C’est essentiellement ce qui est maintenant possible avec la fonctionnalité Ajustement par fractions partielles dans COMSOL Multiphysics® — établir une fonction de transfert numérique via des valeurs complexes en tant que fonction de la fréquence.
Dans le noeud de la fonction PFF, les valeurs sont saisies dans des tables, contenant des nombres réels et imaginaires ainsi que la fréquence. La PFF ajuste ensuite ces valeurs, ce qui donne une version en fractions partielles de la fonction de transfert décrivant le système sous-jacent. La PFF est basée sur un “un algorithme adaptatif d’Antoulas–Anderson (AAA) modifié, AAA2” (disponible dans le COMSOL Multiphysics Reference Manual) avec la forme mathématique:
La première partie est simplement la valeur asymptotique liée à la propriété du système ajusté, nous verrons à l’aide d’exemples comment cela s’articule. La première sommation porte sur tous les pôles à valeur réelle trouvés par la fonction d’ajustement, les résidus étant également réels. La deuxième sommation porte sur les pôles à valeur complexe trouvés par la procédure d’ajustement, les résidus étant également complexes. On constate que les pôles et les résidus complexes sont censés se présenter par paires complexes conjuguées, un pôle complexe étant le jumeau inversé de l’autre. Nous verrons plus loin comment cette hypothèse de symétrie conjuguée sur le résultat de la PFF ne s’étend pas au système d’entrée sous-jacent d’où proviennent les valeurs, il n’y a donc aucune restriction sur le fait que ces systèmes soient réels ou physiquement réalisables.
Il convient également de noter que dans l’expression ci-dessus, x est la fréquence, par opposition à la fréquence angulaire \omega utilisée dans l’explication précédente sur les notions de bases des fonctions de transfert. En outre, les fractions sont toutes du premier ordre avec des constantes dans le numérateur, et donc pour les pôles répétitifs, il peut être nécessaire de reformuler sous la forme montrée précédemment pour illustrer la technique de décomposition en fractions partielles, où le numérateur peut en général avoir des ordres plus élevés. En dehors de cela, la PFF renvoie essentiellement une fonction de transfert numérique sous la forme d’une fraction partielle. Des connaissances fondamentales en traitement du signal seront donc utiles, y compris maintenant, à mesure que nous explorons la fonctionnalité à travers différents exemples.
Pôles réels
Pour voir comment cette fonctionnalité peut être utilisée pour trouver des pôles réels, nous appliquons la PFF à des fonctions de transfert analytiques simples connues afin de nous faire une idée de son fonctionnement et de ce qu’elle renvoie. Tout d’abord, nous testons la sortie de la PFF pour une fonction de filtre passe-bas du premier ordre:
Ici, il existe un pôle réel p = -1, le résidu réel étant 5, lorsque le facteur/coefficient K_\textrm{DC} est absorbé dans le numérateur. Nous allons maintenant voir si la fonction PFF peut le trouver. Connaissant la fonction de transfert, nous pouvons calculer les valeurs réelles et imaginaires de sa réponse en fréquence. Ensuite, nous introduisons ces valeurs dans la fonction PFF. Nous pouvons tracer les valeurs tabulées (marqueurs carrés) avec les valeurs ajustées (ligne continue) et voir si l’ajustement a été fait correctement. Pour ce cas, la correspondance semble parfaite, en revanche il est intéressant de ne pas se contenter d’examiner les courbes, mais d’étudier également les sorties réelles.
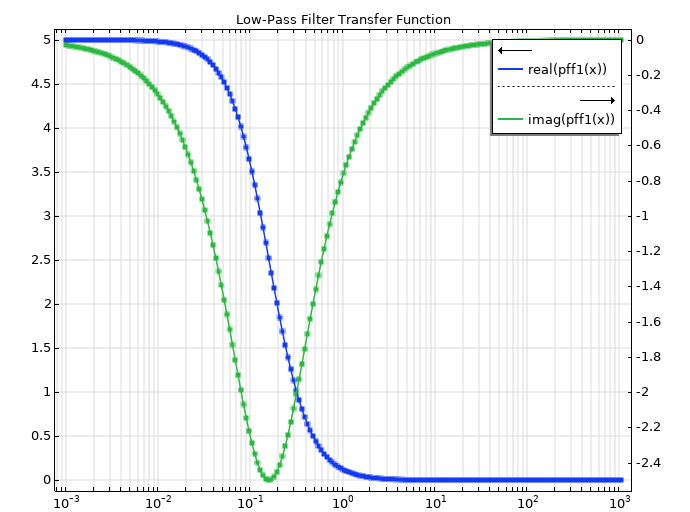
Les résultats PFF présentés sont pour les résidus ajustés et les valeurs des pôles:
| Paramètre | Valeur | Valeur mise à l’échelle par 2\pi |
|---|---|---|
| Y_\infty | 6.547\cdot 10^{-15}+3.78\cdot 10^{-16}i | N/A |
| R_1 | 0.796 | 5 |
| \xi_1 | -0.159 | -1 |
La valeur asymptotique est essentiellement nulle, ce qui est attendu pour ce type de fonction rationnelle. Le pôle est aussi correctement trouvé, puisque x dans la PFF est une fréquence en Hz, et non une fréquence angulaire en radians par seconde, de sorte que le pôle de la fonction de transfert est 2\pi plus élevé que le pôle trouvé via la PFF. Etant donné que cette mise à l’échelle concerne l’ensemble de l’équation, le résidu de 0.796 est inférieur d’environ 2\pi que la valeur attendue 5 \cdot 1, ainsi tout s’accorde avec la mise à l’échelle adéquate.
Un autre cas de pôles réels est étudié avec la fonction de transfert suivante:
Les pôles sont directement visibles dans la fonction de transfert, et nous pouvons calculer les fractions partielles manuellement et obtenir:
Nous nous attendons donc à ce que, après une mise à l’échelle de fréquence, nous obtenions un résidu de 1 pour un pôle \text{p}=-1, et un autre résidu de -1 pour un pôle \text{p}=-2. Et c’est essentiellement ce que nous obtenons:
| Paramètre | Valeur | Valeur mise à l’échelle par 2\pi |
|---|---|---|
| Y_\infty | 7.151 \cdot 10^{-12} – 1.513 \cdot 10^{-11} i | N/A |
| R_1 | -0.159 | -1 |
| \xi_1 | -0.318 | -1.998 |
| R_2 | 0.159 | 1 |
| \xi_2 | -0.159 | -1 |
Le terme asymptotique est essentiellement nul, et si nous multiplions les pôles et les résidus par 2\pi et inversons leur ordre, nous obtenons les valeurs attendues. Les pôles réels multiples sont de ce fait résolus correctement.
Pôles complexes
Un autre exemple s’orientant vers des systèmes plus physiques est celui de la pression émise par le haut-parleur d’un baffle. Le simple circuit réduit est illustré ci-dessous:
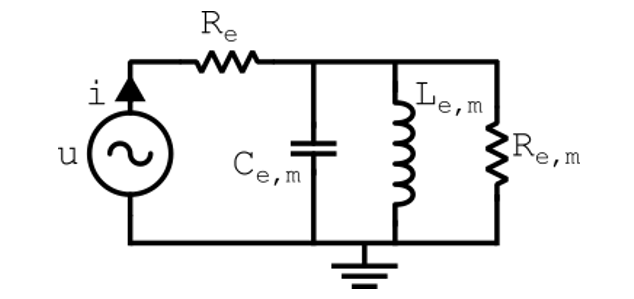
La pression de sortie sera proportionnelle à une fonction de transfert du second ordre donnée comme suit:
avec
et
Le niveau de pression acoustique est indiqué ci-dessous, à la fois pour le transducteur simulé sous-jacent qui sert d’inspiration à notre modèle réduit, et pour les paramètres réduits qui se trouvent dans le tableau ci-dessous.
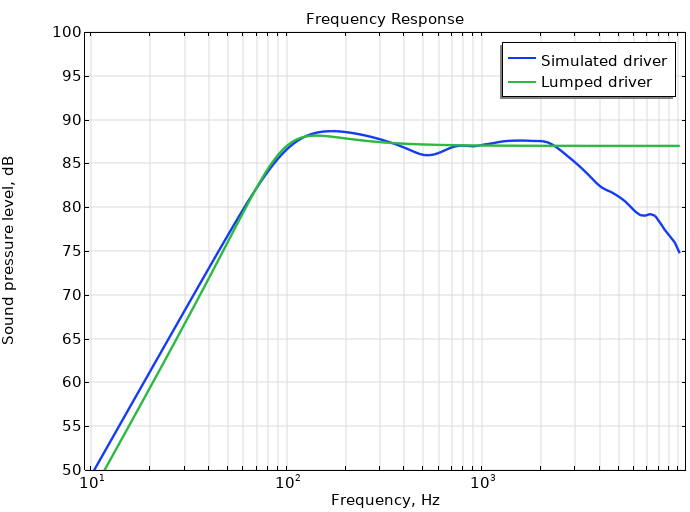
| Paramètre du modèle réduit | Valeur | Unité |
|---|---|---|
| Bl | 5 | T \cdot m |
| R_e | 6 | \Omega |
| M_m | 13 | g |
| K_m | 5 | N/mm |
| R_m | 4 | N\cdot s/m |
| L_{e,m}= Bl^2/K_m | 5 | mH |
| C_{e,m}= M_m/Bl^2 | 520 | \mu F |
| R_{e,m}= Bl^2 /R_m | 6.25 | \Omega |
| \omega_0 | 620 | 1/s |
| Q_t | 0.98722 | 1 |
Avec la valeur Q en question, nous avons garanti des pôles complexes à environ s_{1,2} = -314 \pm 534 i en fréquence angulaire, ou x_{1,2} = -50 \pm 85 i en fréquence régulière. Nous fixons K dans la fonction de transfert à 1, car il s’agit simplement d’une mise à l’échelle de la fonction, puis nous effectuons l’analyse du modèle réduit. La PFF alimentée par les valeurs de la fonction de transfert renvoie les valeurs suivantes:
| Paramètre | Valeur |
|---|---|
| Y_\infty | 1+2.85\cdot 10^{-15} i |
| R_1 | -5.697\cdot 10^{-13} |
| \xi_1 | 99.992 |
| Q_1, Q^\ast_1 | -99.982 \pm 55.744 i |
| \zeta_1, \zeta^\ast_1 | -49.991 \pm 85.108 i |
Le terme asymptotique est fondamentalement égal à un, correspondant à la valeur attendue pour cette fonction de transfert propre, mais pas strictement propre. Il existe un pôle réel et deux pôles complexes. Le pôle réel est considéré comme instable, mais son résidu est si faible qu’il peut simplement être supprimé. Les pôles complexes restants ont des valeurs numériques qui correspondent à la fonction de transfert et, à partir de là, vous pouvez, par exemple, trouver la réponse transitoire à l’aide des résultats de la PFF. La PFF peut également être exécutée sur les données de simulation du transducteur sous-jacent au lieu du modèle réduit. Dans ce cas, davantage de pôles seraient trouvés, mais l’approche serait la même que pour le modèle réduit.
Pôles répétitifs
Les fonctions de transfert peuvent avoir des pôles répétitifs, de sorte que plusieurs pôles résident au même endroit dans le plan-s. Comme indiqué dans la section Décomposition en fractions partielles de cet article de blog, lors de la décomposition en fractions partielles analytiques de ce type de cas, il est courant de diviser la somme en fractions dont certains dénominateurs ont un ordre supérieur à un, alors que la PFF ne renvoie que des fractions de premier ordre. Les valeurs renvoyées par la PFF seront toujours correctes. Cependant leur forte sensibilité constatée impose d’éviter de tronquer les pôles ou les résidus calculés s’ils doivent, par exemple, être exportés et utilisés dans un autre logiciel.
Pôles instables
Lors de l’ajustement par fractions partielles, des pôles instables peuvent être trouvés. Dans ce cas, vous devez d’abord examiner les résidus de ces pôles et les comparer aux résidus des pôles stables. Les pôles instables dont les résidus sont négligeables peuvent être supprimés sans affecter l’ajustement global. Si les pôles instables ont un impact significatif sur la précision de l’ajustement, il convient de s’interroger sur le type de système sous-jacent étudié. Si un système est passif, il est intrinsèquement stable, dans ce cas une bonne compréhension des bases du traitement du signal peut aider à identifier des problèmes liés aux simulations ou aux mesures présentant un comportement instable dans la gamme de fréquences d’intérêt. La fonctionnalité PFF met à disposition l’option Retourner les pôles, qui reflète les pôles instables sur leur position stable dans le plan-s. Cela peut affecter la précision de l’ajustement, mais son effet peut être immédiatement évalué en traçant le nouvel ajustement. Les pôles instables sont souvent situés près des basses fréquences, et leur inversion peut donc n’affecter que légèrement les basses fréquences tout en conservant le comportement des hautes fréquences.
En général, l’inversion des pôles instables affecte la réponse en phase tout en conservant la réponse en amplitude, mais n’oubliez pas que l’hypothèse de causalité doit être prise en compte pour interpréter correctement la stabilité. En outre, le fait que tous les pôles ou la plupart d’entre eux soient instables peut indiquer que les données ajustées correspondent à l’inverse d’une fonction stable, et qu’il peut être judicieux d’évaluer plutôt la fonction inverse.
Il convient de noter que les observations relatives aux pôles instables et/ou aux pôles répétitifs doivent être effectuées pour un plus grand nombre de fonctions de transfert afin de mieux comprendre la fonctionnalité. Les analyses ci-dessus ne doivent donc pas être considérées comme exhaustives, mais plutôt comme introductives. En outre, il peut être utile d’étudier les caractéristiques fondamentales de la passivité des systèmes (Réf. 1 et 2), sans vouloir approfondir les conditions associées dans le présent article, nous indiquerons seulement que cette vérification de la passivité peut généralement être effectuée en vérifiant si toutes les valeurs réelles dans les données ajustées sont positives.
Fonction de transfert irrationnelle: retard temporel
Tous les phénomènes physiques ne sont pas facilement décrits par des fonctions de transfert rationnelles, c’est pourquoi nous allons maintenant examiner dans quelle mesure la PFF s’adapte aux fonctions de transfert non rationnelles. Le premier exemple est un retard de T secondes, qui constitue une fonction de transfert importante sans être sous une forme rationnelle classique:
La fonction de transfert est calculée sur une gamme de fréquence particulière avec un retard d’une seconde, et pour cette gamme de fréquence et pour une tolérance particulière, la PFF renvoie un terme asymptotique d’environ moins un et un seul pôle réel.
| Paramètre | Valeur |
|---|---|
| Y_\infty | -1+3.405 \cdot 10^{-16} i |
| R_1 | 0.6155 |
| \xi_1 | -0.3078 |
Les courbes sont manifestement bien ajustées:
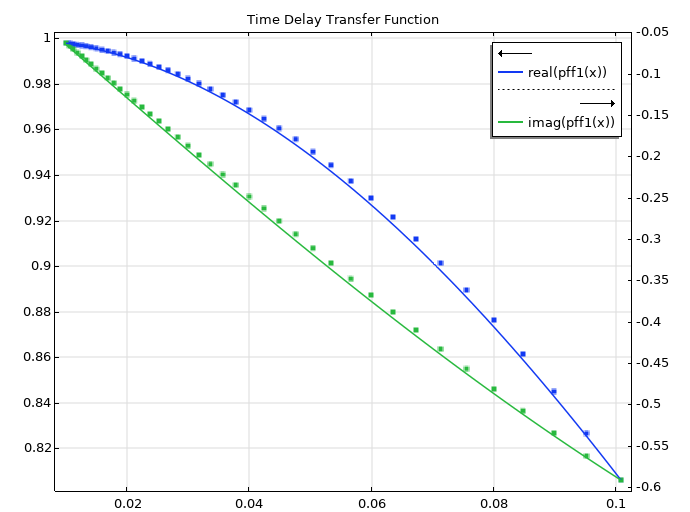
Toutefois, nous pouvons aller plus loin. Sur la base de la valeur asymptotique, nous savons que la fonction de transfert est de type propre. Nous pouvons rassembler les termes et déterminer la fonction de transfert exacte:
En regardant les valeurs numériques, nous pouvons voir que la valeur du résidu est égale à deux fois la valeur du pôle, avec un signe opposé. Ainsi, l’expression ci-dessus peut être réécrite comme suit
Nous constatons maintenant que nous avons obtenu un filtre passe-tout d’ordre 1, ce qui est logique puisque la réponse en amplitude d’un retard temporel doit être plate. Mais nous pouvons aller encore plus loin. Pour un ordre de un dans le numérateur et le dénominateur, nous pouvons simplement trouver l’approximant de Padé P_{1,1}(s) — qui est équivalent à la transformation bilinéaire — pour H(s) = e^{-sT}, avec le résultat:
Ce résultat ressemble beaucoup à celui de la PFF. En effet, en convertissant l’expression ci-dessus au format ix, pour T=1 on obtient:
En considérant 1/\pi = 0.3183, nous pouvons constater que le résultat n’a qu’un faible pourcentage de différence avec ce que la PFF nous a donné. Pour une gamme de fréquences plus large, il faudrait davantage de pôles, et l’on constaterait probablement que les pôles trouvés représentent des racines de polynômes de Bessel (réf. 4).
Fonction de transfert irrationnelle: Microacoustique
La fonction test de transfert irrationnelle suivante est trouvée pour un cas de microacoustique. Considérons une fente rectangulaire dont la section transversale est illustrée ci-dessous (Réf. 5):
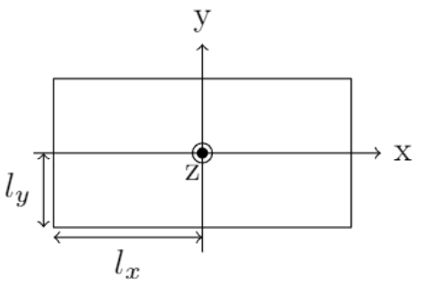
Un tube de cette section aura une impédance acoustique série par unité de longueur, Z^\prime, ainsi qu’une admittance de shunt acoustique par unité de longueur, Y^\prime. Celles-ci ne sont pas directement écrites sous la forme d’une fonction rationnelle, mais elles peuvent être approximées par des composants actifs et réactifs à des fréquences plus basses, il sera intéressant de voir ce qu’il est possible de faire avec la PFF.
Nous supposons que la fente est très mince: l_y \ll l_x. Une telle fente aura une impédance série par unité de longueur comme suit (Réf. 5):
Ici, S = 4l_x l_y est la surface de la fente mince; \rho_0 est la densité de l’air; et x_v = i \omega l^2_y/v, où v = \mu_0 / \rho_0 et \mu_0 est la viscosité de l’air. Une approche pour simplifier cette expression consiste à appliquer un développement de Taylor pour arriver à un modèle réduit comme suit (Réf. 5):
L’impédance série à basse fréquence peut être divisée en une résistance active et constante et une masse réactive et constante. Cela peut être considéré comme une fonction de transfert impropre, mais seulement valable pour les basses fréquences. Voyons plutôt ce que la PFF peut trouver. Une simulation en 2D a été mise en place pour calculer et renvoyer l’impédance en tenant compte des effets acoustiques et microacoustiques sur une gamme de fréquences donnée, révélant ainsi les caractéristiques sous-jacentes du système. Nous devons également choisir des valeurs numériques pour les paramètres géométriques. Ici, l_x est fixé à 1 cm, et l_y est fixé à 0.5 mm. On voit clairement que la couche limite visqueuse varie en fonction de la fréquence et qu’elle couvre l’espace des grandes et petites épaisseurs dans la plage audio pour les dimensions géométriques choisies.

Nous introduisons maintenant l’impédance série calculée par la fonctionnalité PFF. Comme il n’y a pas de zéros ou de pôles explicites à remarquer dans l’expression analytique, nous n’avons pas d’estimation immédiate du résultat de la fonction PFF. La procédure d’ajustement trouve les paramètres appropriés pour les résidus et les pôles afin d’obtenir des courbes adaptées pour l’impédance série, et on peut voir comment la partie réelle se retrouve constante vers les basses fréquences (écoulement de Poiseuille), comme on l’a déjà vu dans le modèle réduit.
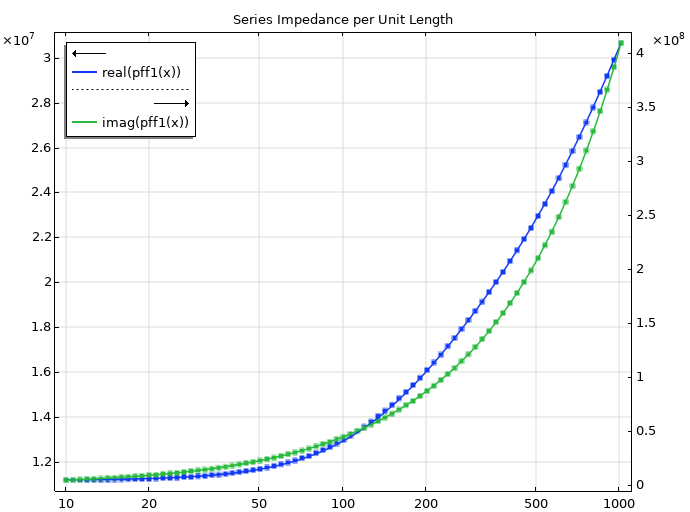
La PFF renvoie une valeur asymptotique finie et trois pôles réels:
| Paramètre | Valeur |
|---|---|
| Y_\infty | 9.336 \cdot 10^{10} + 0.135i |
| R_1 | -1.631\cdot 10^{10} |
| R_3 | -1.901 \cdot 10^9 |
| \xi_1 | -237665.182 |
| \xi_2 | -935.471 |
| \xi_3 | -217.677 |
Connaissant le nombre de pôles que la PFF trouve lors de l’ajustement dans la gamme de fréquences choisie, nous pouvons maintenant essayer de donner un sens à ce résultat. Bien que l’impédance série ne soit pas décrite par une fonction rationnelle mais par une fonction trigonométrique, nous pouvons toujours l’approximer à l’aide d’approximants de Padé. Comme nous avons un terme asymptotique non nul et trois pôles dans la PFF, l’approximant P_{3,3} est celui qu’il faut retrouver:
Ici, a = \rho_0/S et b = l^2_y/v. Si l’on fait le calcul, on obtient essentiellement ce que la PFF a renvoyé.
Bien que l’impédance série par unité de longueur soit connue au préalable de manière analytique en raison de la simplicité de la géométrie, il est très instructif de pouvoir voir la correspondance avec une approche analytique pour établir la fonction de transfert. Mais le cas concret d’utilisation ici est, bien entendu, d’ajuster les résultats numériques pour une simulation donnée sans aucune expression mathématique sous-jacente.
Les fréquences choisies ici sont plutôt basses, il est donc intéressant d’examiner dans quelle mesure l’ajustement peut se faire à des fréquences plus élevées. L’examen du comportement de l’impédance exacte à des fréquences plus élevées montre que la fonction de transfert sous-jacente n’est pas correcte. Étant donné que la fonctionnalité PFF renvoie, de par sa nature, une fonction de transfert ajustée du type propre, nous devrions nous attendre à un écart entre l’impédance exacte et les valeurs ajustées à des fréquences plus élevées en dehors des fréquences d’entrée, c’est ce qui est illustré dans la figure ci-dessous. Tout ajustement ne prendra en considération que la gamme de fréquences fournie pour la PFF, sans aucune garantie quant à l’ajustement en dehors de cette gamme. Ceci est également lié au comportement asymptotique des approximants de Padé, mais nous n’entrerons pas dans ces détails ici. Enfin, il convient de noter que vous pouvez étudier l’inverse de tout système pertinent, ce qui modifiera la propriété d’une fonction de transfert rationnelle, mais même dans ce cas, il faut s’attendre à des écarts en dehors de la gamme de fréquences utilisée dans la procédure d’ajustement.
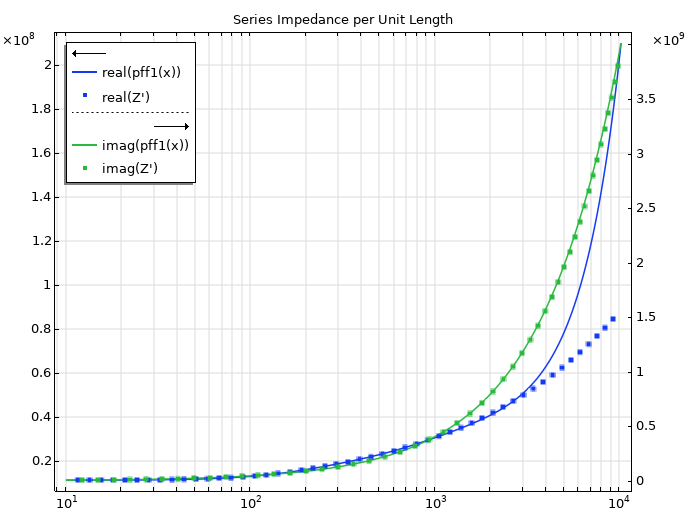
Enfin, un circuit peut être synthétisé à partir des résultats de l’ajustement par fractions partielles, comme indiqué ci-dessous. Ce circuit donnera une approximation de l’impédance série pour une petite longueur de fente, dL, avec la même précision que les pôles et résidus de la PFF dans la même gamme de fréquences. Les détails de cette synthèse dépassent le cadre de cet article de blog, mais il convient de mentionner qu’une admittance de shunt doit également être établie de manière similaire pour une description complète de la fente.
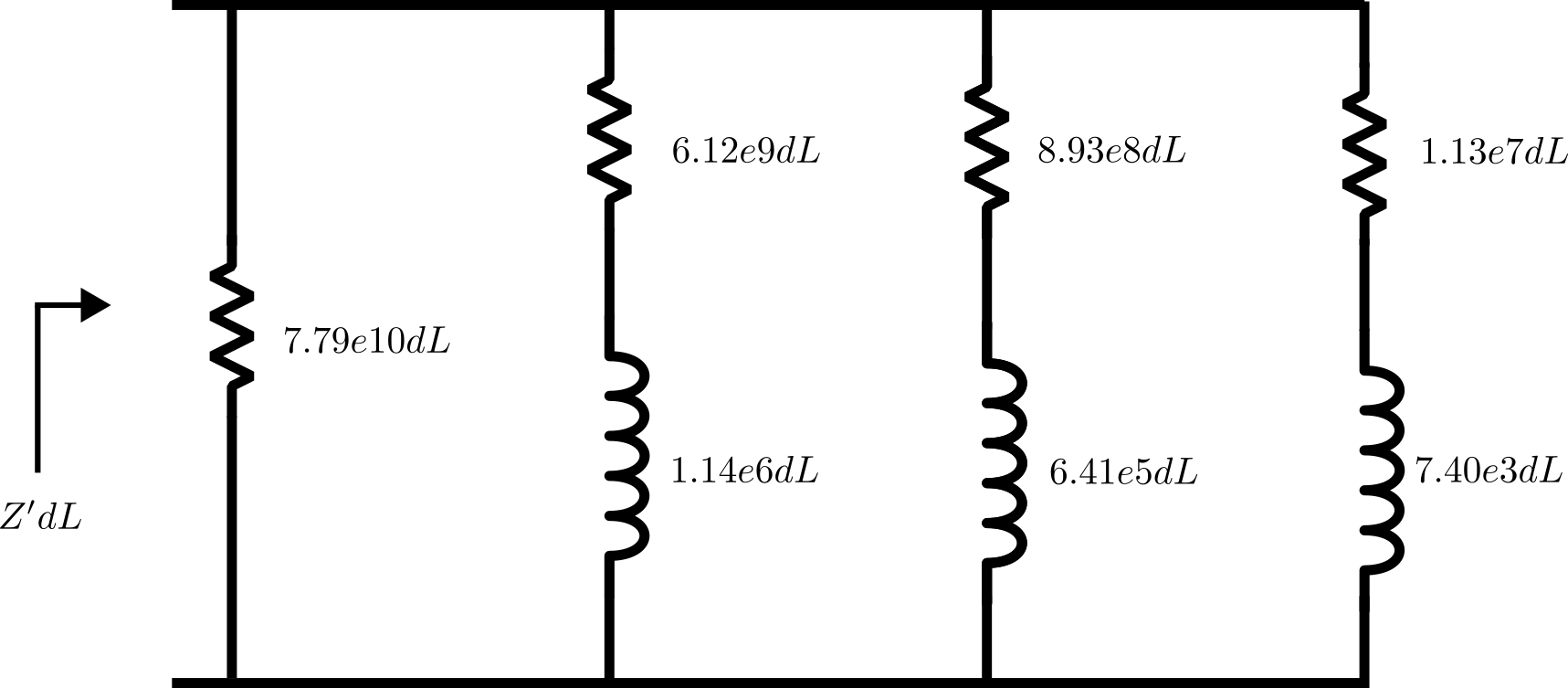
Symétrie conjuguée, fréquences négatives
Comme indiqué précédemment, les pôles complexes de la PFF se présenteront sous la forme de paires complexes conjuguées. Toutefois, il n’y a aucune contrainte explicite sur le fait que le système d’origine soit réel, de sorte qu’il puisse être associé ou non de manière inhérente à une symétrie conjuguée. Comme la PFF elle-même suppose une symétrie conjuguée, il faut limiter la gamme de fréquences pour les valeurs d’entrée à des fréquences positives, incluant éventuellement 0 Hz, ou à des fréquences négatives, incluant éventuellement 0 Hz. La première option est probablement beaucoup plus courante que la seconde, mais les deux sont possibles. Comme les données initiales peuvent ne pas présenter de symétrie conjuguée, les deux options peuvent ne pas conduire au même approximant ajusté.
Conclusion
Nous avons présenté ici le comportement de la nouvelle fonctionnalité Ajustement par fractions partielles dans COMSOL Multiphysics® pour différents scénarios, tels que les fonctions de transfert rationnelles strictement propres, propres et impropres, ainsi que pour des caractéristiques irrationnelles du système telles que les retards temporels, les effets microacoustiques ou les résultats de simulations de couplage multiphysique. La fonctionnalité offre d’excellentes performances et permet un ajustement manuel grâce aux options de modification de la gamme de fréquences et de la tolérance, ainsi que de modification directe des valeurs pour les résidus et les pôles.
Il convient de noter que pour certaines des fonctions de transfert testées avec des pôles réels (sur une gamme de fréquences infinie), la PFF renvoie parfois des pôles complexes dans sa gamme de fréquences finie. Les parties imaginaires étaient alors très petites par rapport à la partie réelle, et il était tout de même aisé de constater que cela avait toujours un sens sur le plan numérique. J’attire votre attention sur ces cas, car ils peuvent être simplifiés davantage en n’incluant que la partie réelle. Il arrive également que les résidus soient très faibles et que le pôle associé n’ait pas beaucoup d’importance ce qui permet de le supprimer de la PFF. Vous pouvez également ajouter ou supprimer des pôles et des résidus et observer l’effet sur les courbes ajustées, ce qui peut être très utile.
Je suis très satisfait de cette fonctionnalité dans la nouvelle version, et je peux imaginer de nombreux cas d’utilisation pertinents.
Découvrez la fonctionnalité d’ajustement par fractions partielles
Vous souhaitez tester vous-même la fonctionnalité Ajustement par fractions partielles? Jetez un coup d’œil au modèle Input Impedance of a Tube and Coupler Measurement Setup: Time Domain MOR using Partial Fraction Fit de la bibliothèque d’applications.
Références
- B. D. O. Anderson and S. Vongpanitlerd, Network Analysis and Synthesis, New Jersey: Prentice-Hall, Inc., 1973.
- Y. Miki, “Acoustical properties of porous material – Modifications of Delany-Bazley models -”, The Journal of the Acoustical Society Japan, vol. 11, no. 1, pp. 19–24, 1990.
- A. V. Oppenheim and R. W. Schafer, Discrete-Time Signal Processing, New Jersey: Prentice Hall, Inc., 1989.
- J. R. Martinez, “Transfer Functions of Generalized Bessel Polynomials”, IEEE Transactions On Circuits And Systems, vol. CAS-24, no. 6, 1977.
- M. R. Stinson, “The propagation of plane sound waves in narrow and wide circular tubes, and generalization to uniform tubes of arbitrary cross-sectional shape”, J. Acoust. Soc. Am. 89 (2), 1991.



Commentaires (0)