La Bibliothèque d'Applications présente des modèles construits avec COMSOL Multiphysics pour la simulation d'une grande variété d'applications, dans les domaines de l'électromagnétisme, de la mécanique des solides, de la mécanique des fluides et de la chimie. Vous pouvez télécharger ces modèles résolus avec leur documentation détaillée, comprenant les instructions de construction pas-à-pas, et vous en servir comme point de départ de votre travail de simulation. Utilisez l'outil de recherche rapide pour trouver les modèles et applications correspondant à votre domaine d'intérêt. Notez que de nombreux exemples présentés ici sont également accessibles via la Bibliothèques d'Applications intégrée au logiciel COMSOL Multiphysics® et disponible à partir du menu Fichier.
This is a tutorial model that demonstrates how to use mesh parameters such as Minimum element size Resolution of curvature Resolution of narrow regions Maximum element growth rate The instructions also detail how to access the mesh statistics and how to create a mesh plot. En savoir plus
The first stop for polluted water entering a water work is normally a large tank, where large particles are left to settle. Generally, gravity settling is an economical method of separating particles. If the fluid in the tank is moving at a controlled low velocity, the particles can be ... En savoir plus
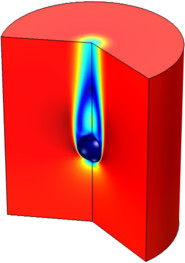
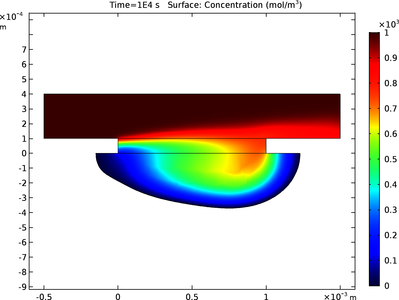
This example illustrates the principle of wet chemical etching for 2D geometry under laminar flow. The purpose of this tutorial is to examine how the copper substrate material is depleted and how the cavity shape evolves during the wet etching process. Wet chemical etching is ... En savoir plus
When designing a concert hall, it is extremely important to take the resonances into account. For a clear and neutral sound, the eigenfrequencies should be evenly spread through the registers. For the home stereo owner, who cannot actually change the shape of his living room, another ... En savoir plus
This model shows how to perform a submodeling analysis in order to evaluate structural stress. Using a submodel helps to compute the results in a refined geometry detail while applying loads and constraints in the global model. En savoir plus
This is a benchmark model for an axisymmetric transient thermal analysis. The temperature on the boundaries changes from 0 degrees C to 1000 degrees C at the start of the simulation. The temperature at 190 s from the anlysis is compared with a NAFEMS benchmark solution. En savoir plus
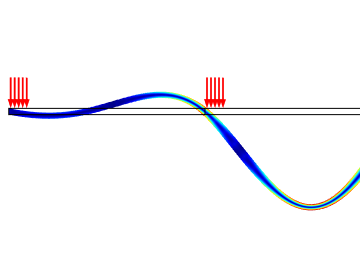
This example shows how to model a load which varies in space and time. A series of load pulses travel along a beam which is supported at equal distances. For some combinations of the traveling speed of the load pulses and the spacing between them, it is possible to excite resonances in ... En savoir plus
Modeling the electrical activity in cardiac tissue is an important step in understanding the patterns of contractions and dilations in the heart. The heart produces rhythmic electrical pulses, which trigger the mechanical contractions of the muscle. A number of heart conditions involve ... En savoir plus
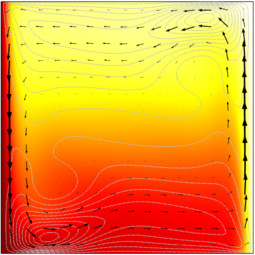
This model couples the Navier Stokes equations and the heat transfer equations to examine density driven flow of free fluids. Here the fluid is in a square cavity with a heated wall. The buoyancy force is a Boussinesq term added to the Navier-Stokes equations. The equation is ... En savoir plus
Large FEM simulations can be costly and, if repeated simulations are needed, it can be beneficial to use reduced-order models (ROMs). ROMs are typically valid only in the vicinity of their design conditions and have lower accuracy, but the simulation time is significantly shorter. The ... En savoir plus