- Bridging the Terahertz Gap
- Modeling the Lithium-Ion Battery
- Protection contre la Corrosion
- Modélisation des batteries
- Modélisation et Simulation dans le développement des piles à combustible
- Modélisation thermique des petits satellites
- Analyse électro-vibroacoustique d'un transducteur à armature équilibrée
FEM Convergence for PDEs with Point Sources in 2-D and 3-D
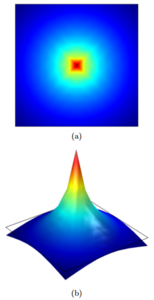
Numerical theory provides the basis for quantification of the accuracy and reliability of a FEM solution by error estimates on the FEM error vs. the mesh spacing of the FEM mesh. This paper presents techniques needed in COMSOL Multiphysics® software to perform computational studies for elliptic test problems in two and three space dimensions that demonstrate this theory by computing the convergence order of the FEM error. We show how to perform these techniques for a problem involving a point source modeled by a Dirac delta distribution as forcing term. This demonstrates that PDE problems with a non-smooth source term necessarily have degraded convergence order compared to problems with smooth right-hand sides and thus can be most efficiently solved by low-order FEM like linear Lagrange elements.
Téléchargement
- graf_presentation.pdf - 0.44MB
- graf_poster.pdf - 0.97MB
- graf_paper.pdf - 0.49MB
- graf_abstract.pdf - 0.12MB
