
Analyser le comportement mécanique des cellules pour des applications biologiques
Aujourd’hui, notre invité Björn Fallqvist de Lightness by Design, un consultant certifié COMSOL, aborde l’utilisation de la simulation pour mieux comprendre le comportement mécanique des cellules.
Les cellules biologiques sont essentielles à la vie telle que nous la connaissons. Non seulement elles stockent et répliquent les informations héréditaires sous forme d’ADN, mais jouent également un rôle déterminant dans les processus biologiques. Dans la plupart, voire la totalité de ces processus, le comportement mécanique des cellules est un facteur essentiel pour un fonctionnement physiologique normal.
L’importance des cellules biologiques
Naturellement, nous ne pourrions pas exister ni fonctionner sans cellules. Les vertébrés utilisent la circulation des globules rouges, les érythrocytes, pour acheminer l’oxygène vers les tissus biologiques. Les fibroblastes utilisent leur mécanisme de contraction pour migrer vers — et déclencher le processus de cicatrisation — des plaies. Les cellules endothéliales qui tapissent nos vaisseaux sanguins servent de barrières de filtration. Ces cellules s’appuient non seulement sur des mécanismes biochimiques/de transport, mais aussi sur leur comportement mécanique pour assurer des fonctions physiologiques normales.
L’entité structurelle responsable de la rigidité cellulaire est un réseau interconnecté appelé cytosquelette, visible sur l’image ci-dessous. Ce cytosquelette se compose principalement de trois types de filaments polymérisés, chacun ayant sa propre structure et ses propres caractéristiques mécaniques:
- Actine
- Filaments intermédiaires
- Microtubules
Cette base complexe permet aux cellules d’adapter leurs propriétés mécaniques à leur environnement, tant instantanément qu’au cours du temps.
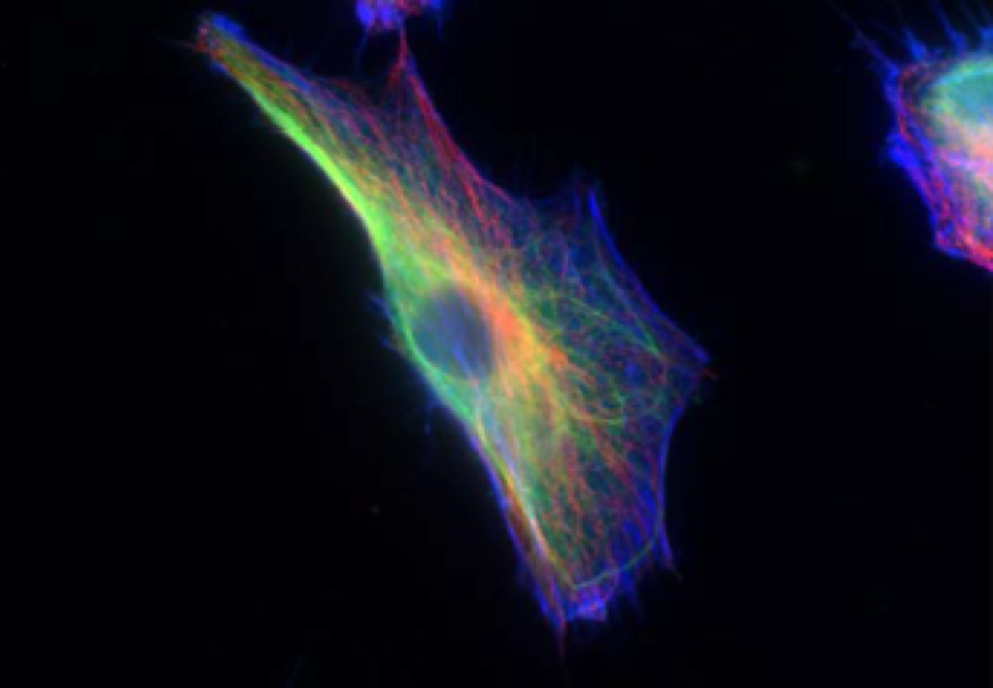
Une cellule fibroblaste où on visualise le cytosquelette, comprenant l’actine (en bleu), les filaments intermédiaires (en vert), et les microtubules (en rouge). Image utilisée avec l’autorisation de Rathje et al. tirée de l’article “Oncogenes induce a vimentin filament collapse mediated by hdac6 that is linked to cell stiffness”.
Les cellules et les réseaux cytosquelettiques sont tous deux hautement viscoélastiques, comme vous pouvez le voir dans le graphique ci-dessous représentant une courbe de relaxation issue d’une expérience d’indentation cellulaire réalisée par microscope à force atomique (AFM).
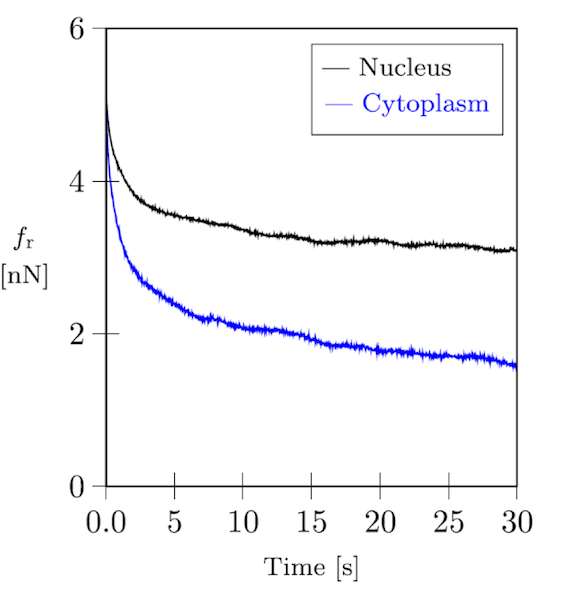
Courbe de relaxation de force d’un fibroblaste.
Il existe de nombreux exemples dans lesquels une cellule malade présente des propriétés mécaniques anormales, favorisant la progression de la pathologie. Le cytosquelette présent dans ces cellules se comporte souvent différemment de celui des cellules saines. Par exemple, les cellules cancéreuses sont connues pour présenter des variations de rigidité importantes par rapport aux cellules témoins. Dans de nombreux cas, cela peut être lié au cytosquelette. Le réseau de filaments intermédiaires pourrait s’effondrer autour du noyau ou il pourrait y avoir une propagation cellulaire accrue (étroitement liée au cytosquelette d’actine par le biais d’adhésions focales).
Étude du comportement mécanique des filaments et des cellules
Comme mentionné précédemment, le cytosquelette est une entité dynamique capable de se remodeler à une échelle de temps allant de quelques millisecondes à plusieurs heures. Il en résulte un comportement viscoélastique prononcé, dû à la nature des réseaux qui le composent. Une solution de filaments d’actine, par exemple, se comporte comme un solide à court terme et comme un liquide à plus long terme. Cela est dû au lien entre les fluctuations thermiques des filaments semi-flexibles et leur propension à glisser les uns entre les autres; c’est-à-dire qu’ils sont plus ou moins contraints cinématiquement à court terme. La température est également un facteur important, en partie parce qu’elle affecte le comportement thermique, mais aussi en raison des diverses protéines de liaison présentes dans la solution.
Si l’on considère conjointement le comportement mécanique de ce type de réseau de polymères sous-jacent et les autres constituants cellulaires (par exemple, le noyau et la membrane cellulaires), il est évident qu’une analyse détaillée tenant compte de tous ces facteurs est pratiquement impossible. Il est toutefois possible de contourner cette difficulté et d’obtenir des résultats en considérant la cellule à une échelle macroscopique.
En créant un modèle par éléments finis dans le logiciel COMSOL Multiphysics® software, vous pouvez ignorer la structure intracellulaire hétérogène et la considérer comme un continuum, c’est-à-dire que le champ de déplacement est continu. Il s’agit d’une approximation acceptable si votre objectif est de quantifier la réponse macroscopique des cellules à des stimuli externes.
Le modèle décrit dans cet article de blog est celui d’un essai de relaxation. Un indenteur rigide est enfoncé dans la cellule viscoélastique molle, puis la relaxation de la force d’indentation qui en résulte est mesurée et comparée aux données expérimentales.
Modèle numérique d’une cellule
Un modèle de cellule aux dimensions typiques est présenté ci-dessous. Notez que le domaine est créé autour de la ligne centrale. La section semi-circulaire correspond au noyau cellulaire, qui influera également sur la réponse mécanique. Dans cette analyse, nous construisons aussi un indenteur dans la géométrie et négligeons la membrane cellulaire. Pour simplifier, nous effectuons une analyse 2D en supposant que la cellule est axisymétrique.
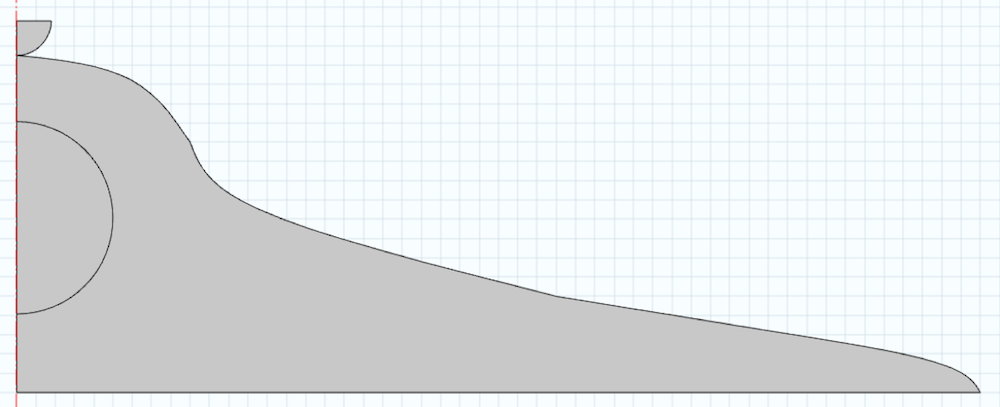
Le modèle est maillé avec des éléments 2D en raffinant la taille sous l’indenteur.
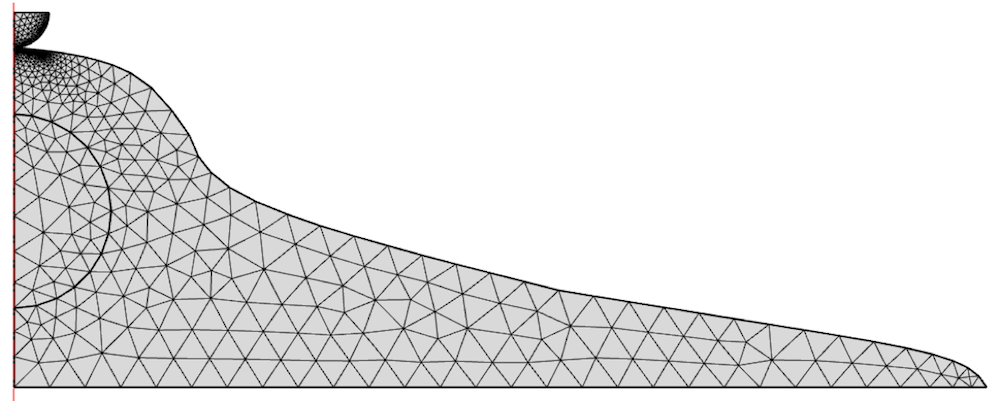
Le choix de la loi de comportement matériau pour le cytoplasme et le noyau de la cellule doit refléter à la fois la réponse instantanée et la réponse à long terme du matériau. Un modèle élastique linéaire est beaucoup trop simple, car les cellules peuvent généralement supporter des déformations importantes et présenter un écrouissage significatif. Pour la réponse du cytoplasme, nous pouvons choisir une loi de comportement hyperélastique simple, le modèle néo-Hookéen, dans lequel les contraintes et les déformations sont calculées à partir d’une fonction de densité d’énergie de déformation Ψ sous la forme
Dans cette forme, où le matériau est supposé (quasi) incompressible, le module de cisaillement µ, la variation élastique du volume Jel, le module de compressibilité κ, et la première invariante isochore \overline{I}_1 sont inclus. Afin d’intégrer le comportement viscoélastique, deux branches Maxwell généralisées sont également incluses. Le noyau s’est avéré être principalement élastique et est donc modélisé sans branches viscoélastiques.
Les paramètres des matériaux choisis sont indiqués dans ce tableau:
| Domaine | Module de cisaillement |
Module de compressi- bilité |
Facteur d’énergie 1 | Temps de relaxation 1 | Facteur d’énergie 2 | Temps de relaxation 2 |
|---|---|---|---|---|---|---|
| Noyau | 1.667 kPa | 5000 kPa | N/A | N/A | N/A | N/A |
| Cytoplasme | 0.155 kPa | 1000 kPa | 10 | 0.5 s | 10 | 50 s |
Le bas de la cellule est contraint verticalement. Alors qu’en réalité, la cellule adhère au substrat par le biais d’adhésions focales, cela ne devrait être qu’un effet local qui n’influence pas significativement la réponse en termes de force.
Le contact entre l’indenteur et la cellule est imposé par une formulation de pénalité, en utilisant l’indenteur comme frontière source. Le domaine de l’indenteur se voit attribuer une vitesse de 0.1 µm/s, jusqu’à ce que le déplacement vertical total atteigne 4.6 µm. Il est ensuite maintenu fixe pendant le reste de l’analyse, jusqu’à une durée totale de 30 s.
Résultats de simulation
La déformation locale de la cellule après indentation est illustrée dans le graphique ci-dessous.
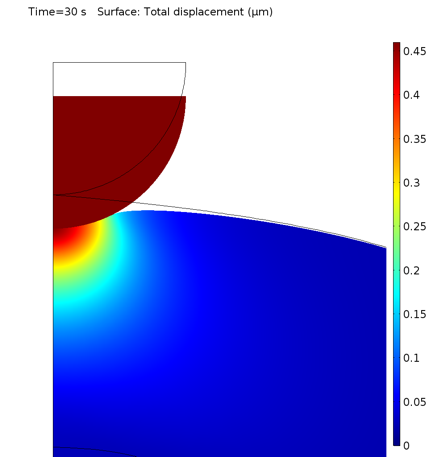
Déformation de la cellule sous l’indenteur.
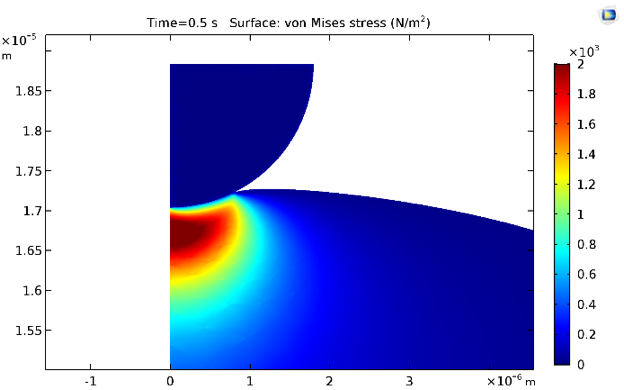
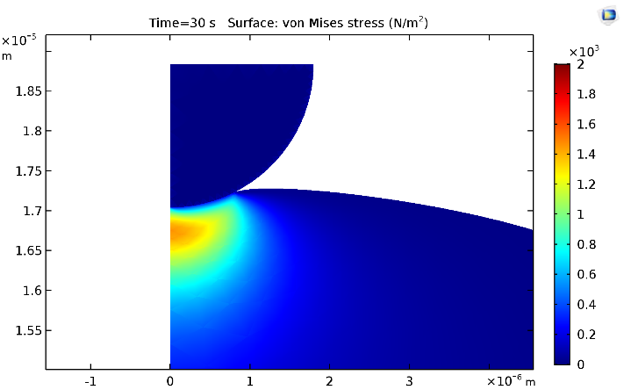
Les contraintes équivalentes de von Mises aux instants 0.5 s et 30 s sont indiquées ci-dessous. Naturellement, les contraintes diminuent en raison de la relaxation des contraintes due à l’inclusion de branches viscoélastiques dans la loi de comportement matériau du cytoplasme.
Distribution des contraintes à 0.5 s (à gauche) et à 30 s (à droite).
La force de réaction verticale sur l’indenteur peut être extraite de COMSOL Multiphysics et comparée aux données expérimentales.
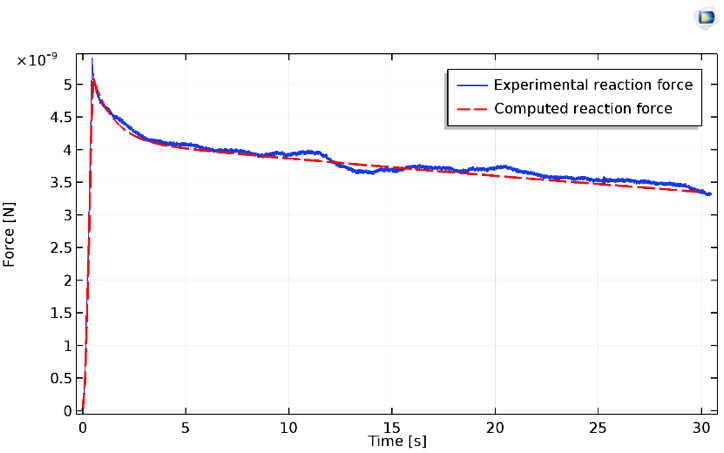
Résultats relatifs à la force d’indentation de la cellule, expérimentaux (en bleu) et calculés (en rouge).
Mesurée à l’aide d’expériences, la relaxation présente généralement au moins deux régimes distincts. Ces valeurs sont raisonnablement bien prédites par le modèle néo-Hookéen simple, avec ses deux branches viscoélastiques. Il convient de noter que le régime d’indentation initial présente un durcissement important avant la pente constante (visible dans le graphique ci-dessus).
Conclusions sur la modélisation biomécanique
Comme nous venons de le voir, COMSOL Multiphysics permet de reproduire facilement le comportement viscoélastique des cellules à l’aide de lois de comportement matériau (relativement) simples. Bien entendu, il est possible d’obtenir un niveau de complexité plus élevé en utilisant des modèles de matériaux plus sophistiqués. Dans ce cas, l’utilisation d’autres modèles hyperélastiques, tels que les modèles Mooney-Rivlin ou Ogden, en combinaison avec un plus grand nombre de branches viscoélastiques, peut donner des résultats encore plus précis. Gardez à l’esprit que plus le nombre de paramètres matériau nécessaires est élevé, plus il faut disposer de points de données expérimentales pour le matériau en question.
La cellule est en réalité un système bien plus complexe que celui modélisé ici. Il existe un échange constant de signaux mécaniques et biochimiques qui modifient en permanence la structure intracellulaire, la forme de la cellule et son comportement locomoteur. Il va sans dire que modéliser la cellule comme un continuum est une simplification majeure, mais une telle approximation peut s’avérer très utile dans de nombreux cas. Si nous devions analyser des cellules métastatiques, par exemple, il suffirait peut-être de caractériser leur rigidité macroscopique afin d’évaluer leur capacité à se faufiler à travers les tissus ou les artères. Dans un tel cas, la rigidité de la cellule dans son ensemble par rapport à l’obstacle serait le facteur déterminant, et non les interactions détaillées entre, par exemple, le cytosquelette et le noyau cellulaire.
Il convient également de mentionner que la cellule, en plus d’être un système complexe, est loin d’être déterministe et ne peut être caractérisée de manière unique par un ensemble de paramètres géométriques et matériels. La réponse des cellules individuelles varie en fonction de leur état de santé, de leur état de locomotion et de leur cycle cellulaire, entre autres facteurs. Pour évaluer correctement la réponse mécanique d’un type de cellule de manière expérimentale, il faudrait examiner un plus grand nombre de cellules individuelles. Nous nous contentons toutefois d’évaluer la capacité à modéliser la réponse d’une cellule individuelle.
D’une manière générale, les lois de comportement hyperélastique peuvent souvent servir à modéliser les cellules mais aussi d’autres matériaux biologiques. En fonction du matériau et de l’échelle de temps, le comportement viscoléastique peut également être pris en compte. Cela ouvre des perspectives intéressantes dans le domaine de la modélisation biomécanique.
Par exemple, l’athérosclérose est une pathologie cardiovasculaire courante dans laquelle les globules blancs s’accumulent sur la paroi artérielle, réduisant ainsi le flux sanguin et augmentant le risque de crise cardiaque due à un caillot sanguin. L’angioplastie est une intervention courante visant à soulager cette pathologie. Elle consiste à insérer un ballonnet dans l’artère et à le gonfler. Souvent, un stent mécanique est ensuite utilisé pour stabiliser la section artérielle. À l’aide de COMSOL Multiphysics, nous avons pu capturer le comportement hyperélastique-viscoélastique de la paroi artérielle ainsi que les caractéristiques composites dues à l’orientation des fibres de collagène, et calculer le développement et l’évolution instantanée et transitoire des contraintes et des déformations.
Note de l’éditeur, 8/20/18: Le fichier correspondant au modèle de relaxation cellulaire a été ajouté à l’Echange d’applications. Vous pouvez y accéder ici.
A propos de l’auteur
Björn Fallqvist est un consultant de Lightness by Design et travaille dans le domaine du développement de produits basé sur l’analyse numérique. Il a obtenu un doctorat du Royal Institute of Technology en 2016, où il a travaillé sur le développement de modèles permettant de décrire le comportement mécanique des cellules biologiques. Son principal intérêt professionnel et sa spécialisation portent sur la caractérisation des matériaux et l’utilisation de diverses lois de comportement matériau pour capturer les phénomènes physiques.
Références
- Rathje et al, “Oncogenes induce a vimentin filament collapse mediated by hdac6 that is linked to cell stiffness”, Proceedings of the National Academy of Sciences, 111, pp. 1515–1520, 2014.
- B. Fallqvist et al., “Experimental and computational assessment of F-actin influence in regulating cellular stiffness and relaxation behaviour of fibroblasts”, Journal of the Mechanical Behavior of Biomedical Materials, Vol 59, pp. 168–184, 2016.




Commentaires (0)