
Comprendre les options d’excitation pour la modélisation des courants électriques
Si vous utilisez l’interface physique Courants électriques dans COMSOL Multiphysics® pour modéliser le chauffage électromagnétique, vous avez peut-être remarqué qu’il existe de nombreuses façons différentes d’exciter un modèle, en particulier dans le domaine fréquentiel. Vous avez la possibilité de spécifier le courant, la tension et deux façons différentes de spécifier la puissance ainsi que la connexion à un circuit. Nous allons ici approfondir cette thématique et voir comment choisir entre ces différentes options.
Table des matières
- Introduction
- Excitation en puissance de terminal
- Excitation en courant imposé
- Pourquoi les pertes varient-elles avec la fréquence?
- Excitation en tension
- Remarque importante à propos de l’isolation
- Connexion à l’interface physique Circuit électrique
- Dépôt d’une puissance fixe dans le modèle
- Conclusion
Introduction
L’exemple sur lequel nous allons nous baser est présenté ci-dessous: il s’agit d’un modèle de câble coaxial inséré dans une cavité métallique contenant un diélectrique à pertes avec une permittivité relative de 50 et une conductivité électrique de 30 mS/m.
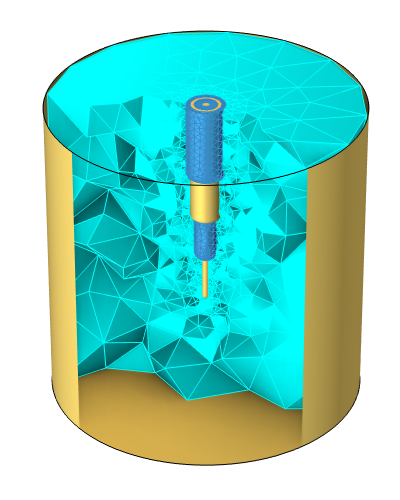
Câble coaxial inséré dans une cavité métallique contenant un matériau diélectrique à pertes.
Nous avons détaillé ce modèle dans un article précédent, où nous avons décrit les différentes approches de modélisation qui permettent de le résoudre. Toutes ces approches donnent des résultats presque identiques dans le domaine des basses fréquences, mais peuvent commencer à présenter des écarts à des fréquences plus élevées. Sur la base de ces observations, nous exploiterons le modèle dans la plage de fréquences 1–100 MHz, puis nous comparerons l’interface physique Courants électriques à l’interface physique Ondes électromagnétiques. Comme nous l’avons vu précédemment, nous devrions obtenir une très bonne concordance sur cette plage. Dans les deux interfaces, nous résoudrons les champs à l’intérieur du diélectrique à pertes ainsi que de l’isolant, et supposerons que l’épaisseur de peau est suffisamment faible à l’intérieur des conducteurs coaxiaux métalliques pour que ceux-ci puissent être modélisés via des conditions aux limites.
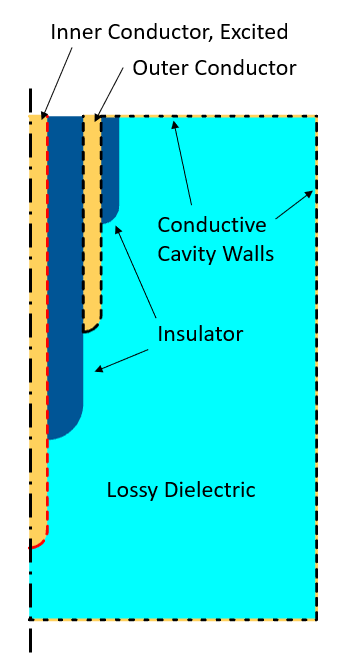
Schéma du modèle.
La figure ci-dessus met en évidence les conditions aux limites. Le conducteur interne excité est représenté par une ligne en tirets rouges, toutes les frontières de ce conducteur sont connectées électriquement. Le conducteur externe et les parois conductrices de la cavité, ainsi que la frontière de l’isolant qui les sépare, sont également connectés électriquement. L’objectif ici est de justifier davantage l’utilisation de l’interface physique Courants électriques pour ce type de modélisation. Pour utiliser correctement cette interface, nous devons toutefois prendre le temps de comprendre les différentes options d’excitation.
Excitation en puissance de terminal
Nous commençons par exciter le modèle avec la condition aux limites Terminal, de type Terminé, qui nous permet de spécifier une puissance et une impédance caractéristique. Cette condition aux limites imite une connexion à une alimentation électrique via une ligne de transmission infinie sans perte, d’impédance caractéristique connue, telle qu’un câble coaxial de 50 ohms. L’alimentation électrique fournit à l’infini un signal sinusoïdal, avec une puissance moyenne sur un cycle qui est constante. Ce signal se propage le long de la ligne de transmission sans perte et dans le modèle de Courants électriques, où il est partiellement réfléchi dans la ligne de transmission et partiellement dissipé dans le modèle. La composante réfléchie se propage en sens inverse le long de la ligne de transmission infinie sans perte et n’interagit pas avec l’alimentation électrique. La puissance spécifiée doit toujours être supérieure ou égale à zéro, et cette puissance sera dissipée dans le modèle, réfléchie dans le terminal terminé ou transmise vers une autre condition aux limites.
La condition Terminal doit être utilisée conjointement avec une autre condition qui fixe le potentiel électrique ailleurs dans le modèle. Une condition Masse est typiquement utilisée. Nous avons déjà abordé le concept de masse, et il convient de rappeler que tout ensemble de frontières connectées électriquement peut être défini comme une condition aux limites de masse. Dans ce modèle, nous choisirons de définir la masse par le conducteur extérieur et les parois de la cavité, ainsi que la frontière entre les deux. Autrement dit, le conducteur extérieur et les parois de la cavité sont connectés électriquement et maintenus à un potentiel électrique nul.
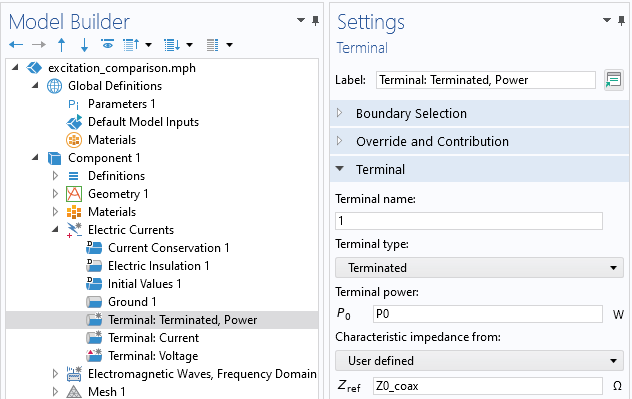
Vue de la condition Courants électriques, Terminal , de type Terminé. Champ de saisie de l’impédance de la ligne de transmission et la puissance fournie.
Considérons le signal provenant de l’alimentation électrique le long de la ligne de transmission: une partie du signal sera réfléchie vers l’alimentation électrique, qui contient un isolateur ou un circulateur pour protéger l’appareil. Idéalement, cette réflexion est minimale, ce qui permet de transférer autant d’énergie que possible vers le matériau à chauffer. L’amplitude de cette réflexion est quantifiée par le paramètre S, qui est calculé automatiquement par cette condition aux limites.
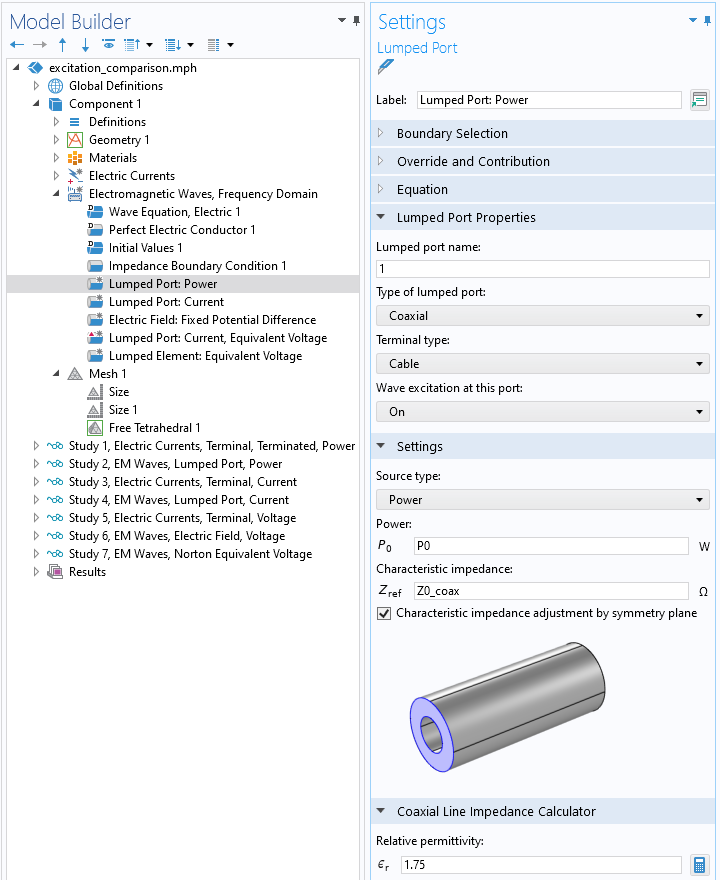
Vue de la condition Ondes électromagnétiques, Port réduit, de type Coaxial avec une source de type Puissance. L’impédance du câble est une donnée d’entrée, bien qu’elle puisse également être calculée à partir de la géométrie.
Nous comparons cela avec une condition aux limites équivalente dans la formulation Ondes électromagnétiques. Ici, nous raisonnons en termes d’ensembles de frontières des domaines connectés électriquement. Dans notre modèle en domaine fréquentiel, il existe deux ensembles de frontières de ce genre: le conducteur externe, qui est connecté électriquement aux parois de la cavité et le conducteur interne comme le montre le schéma ci-dessus. Ces derniers sont électriquement séparés par l’espace annulaire à l’intérieur du câble coaxial, et c’est au niveau de cette frontière annulaire que nous appliquons le Port réduit, de type Coaxial, et que nous spécifions à nouveau la puissance et l’impédance du câble. L’interprétation physique reste la même que précédemment, et cette condition aux limites calculera également le paramètre S.
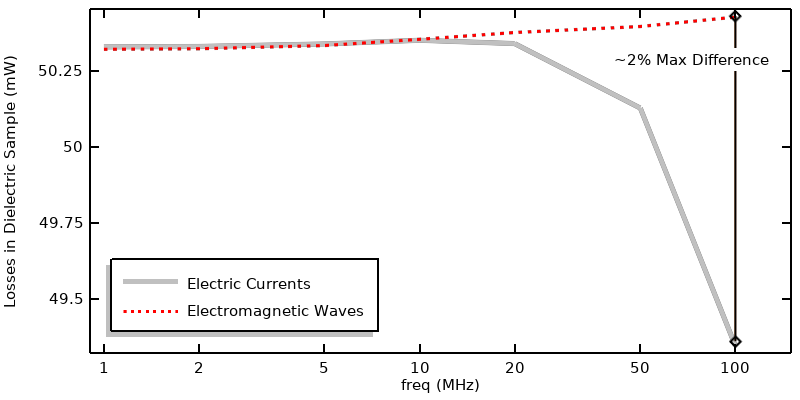
Comparaison des pertes calculées en utilisant les interfaces Courants électriques et Ondes électromagnétiques avec une excitation en puissance.
Nous pouvons comparer les deux approches en termes de chaleur déposées dans un matériau à pertes dans la figure ci-dessus. Celle-ci montre une excellente concordance sur la majorité de la plage de fréquences. Elles commencent à diverger à des fréquences plus élevées, ce qui s’explique par le fait que l’interface physique Ondes électromagnétiques considère également les effets inductifs, et pas seulement les effets résistifs et capacitifs pris en compte par l’interface Courants électriques.
Il est important de comprendre la signification physique de la condition Terminal de type Puissance dans l’interface Courants électriques ainsi que la condition Port réduit dans l’interface Ondes électromagnétiques. Elles sont destinées à modéliser une connexion à une ligne de transmission infinie sans pertes, avec une source d’alimentation à l’infini qui envoie une onde — un signal — qui se propage le long de la ligne. Ce signal est partiellement dissipé dans le modèle sous forme de chaleur, et partiellement réfléchi dans la ligne infinie, où il continue sans jamais interférer avec la source d’alimentation. En réalité, bien évidemment, le signal réfléchi interférerait avec la source, et les systèmes à haute fréquence peuvent présenter des réflexions importantes en cas de désadaptation d’impédance. Les sources sont donc équipées d’isolateurs ou de circulateurs afin d’empêcher les réflexions de signaux d’endommager l’alimentation électrique. A des fréquences plus basses, la longueur d’onde caractéristique étant plus grande que la taille totale du système, nous ne pouvons plus considérer les excitations en termes d’ondes, et nous nous tournons donc vers d’autres conditions d’excitation.
Excitation en courant imposé
Nous passons à l’excitation du modèle Courants électriques avec un Terminal de type Courant pour modéliser une source qui impose un courant connu. Bien que physiquement, il existe toujours une ligne de transmission connectant la source au modèle, nous ne considérons plus aucun signal réfléchi vers la source. Notez qu’il est raisonnable de spécifier une valeur négative ou complexe pour le courant dans un modèle dans le domaine fréquentiel. Une valeur complexe, ou négative, signifie simplement une excitation avec un déphasage, comme décrit ici. Ce courant circulera à travers le modèle, et ensuite à travers la condition aux limites Masse ou toute autre condition aux limites qui fixe le potentiel électrique.
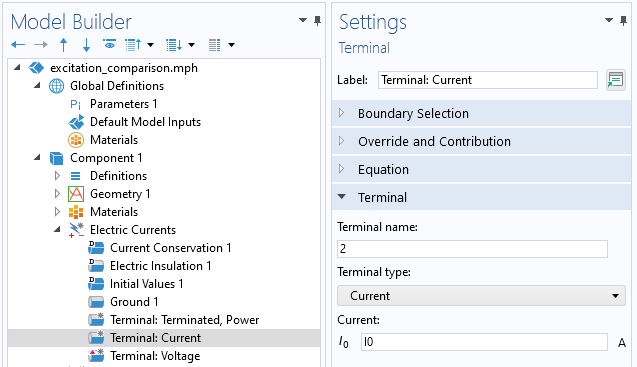
Vue de la condition Courants électriques, Terminal , de type Courant.
La condition équivalente dans l’interface Ondes électromagnétiques est Port réduit de type courant, comme illustré dans la capture d’écran ci-dessous.
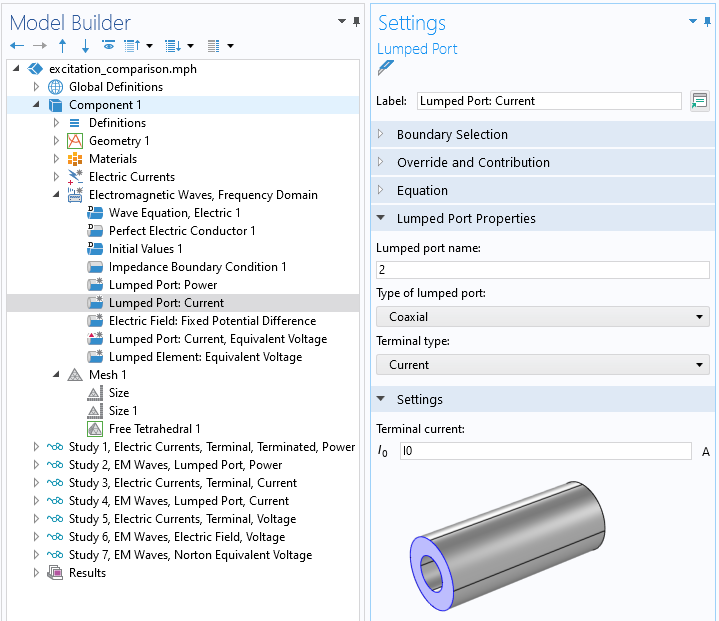
Vue de la condition Ondes électromagnétiques, Port réduit, de type Coaxial avec une excitation en Courant.
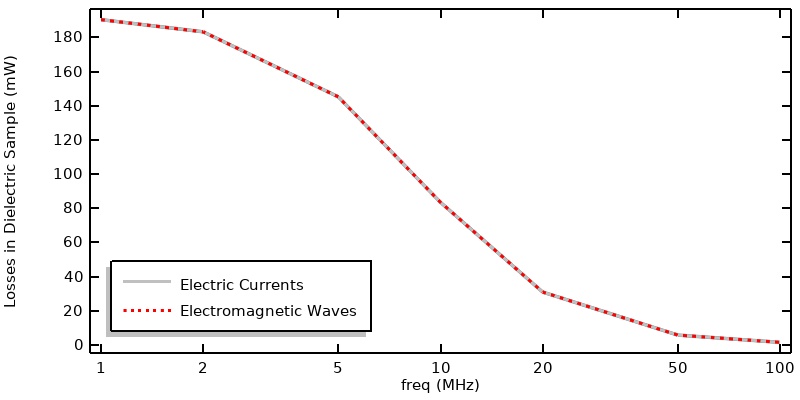
Comparaison des résultats lors de l’excitation par un courant.
La comparaison des deux approches est illustrée dans le graphique ci-dessus, et l’on observe une excellente concordance. Ce qui est sensiblement différent de l’approche précédente utilisant l’excitation en puissance, est que les pertes varient beaucoup plus fortement en fonction de la fréquence. Cela mérite une attention particulière.
Pourquoi les pertes varient-elles avec la fréquence?
Pour un problème piloté par le courant, avec un courant de crête I_0, nous pouvons calculer les pertes moyennes sur un cycle dans l’ensemble du modèle à partir de l’équation
où Z_s est l’impédance du système, perçue du point de vue du terminal. L’impédance est une des données de sortie calculées automatiquement par la condition de type Terminal, Courant et la condition Ondes électromagnétiques, Port réduit. Le tableau ci-dessous présente les valeurs sur la plage de fréquences considérées:
| Fréquence (MHz) |
Courants électriques Impédance (Ohms) |
Ondes électromagnétiques Impédance (Ohms) |
|---|---|---|
| 1 | 3807.2-436.4i | 3807.0-436.3i |
| 2 | 3664.6-840.0i | 3664.3-839.8i |
| 5 | 2903.6-1663.2i | 2903.5-1662.9i |
| 10 | 1668.4-1909.9i | 1668.4-1909.4i |
| 20 | 618.13-1414.1i | 618.19-1413.3i |
| 50 | 114.38-653.8i | 114.48-652.2i |
| 100 | 29.249-334.4i | 29.367-331.1i |
Tableau d’impédance en fonction de la fréquence pour les deux formulations.
Ces données montrent que la partie réelle de l’impédance diminue avec la fréquence, tandis que la partie imaginaire devient plus négative. Autrement dit, ce système devient moins dissipatif et plus capacitif à des fréquences plus élevées.
Nous devons chercher une explication simple à cette tendance. Ignorons donc toutes la complexité géométrique et considérons ce modèle uniquement en termes d’un seul matériau placé entre deux électrodes. Nous pouvons considérer ce cas, de la manière la plus simplifiée, comme un circuit RC parallèle, où la résistance et la capacité sont respectivement liées à la conductivité et la permittivité du matériau. Le courant traversant ces deux chemins parallèles — les courants de conduction étant dus à la conductivité du matériau et les courants de déplacement dus à la permittivité — variera en fonction de la fréquence. A des fréquences plus élevées, le courant de déplacement sera plus important que le courant de conduction, de sorte que le rapport entre l’amplitude de la partie complexe de l’impédance et la partie réelle de l’impédance augmente.
Grâce à cette compréhension de l’impédance et de sa variation en fonction de la fréquence, nous pouvons également expliquer pourquoi l’excitation en puissance se comporte différemment selon la fréquence. L’excitation en puissance représente plutôt un signal entrant qui est partiellement réfléchi hors de, et partiellement absorbé par, le modèle. La réflexion est donnée par le paramètre S. Pour un système à un port, cela peut être calculé à partir de Z_s et Z_0, l’impédance du câble:
et, pour un système à un port, la puissance absorbée à l’intérieur du système est donnée par
Pour ce système, qui présente une forte désadaptation d’impédance entre le câble et le segment de matériau chauffé, une grande partie de la puissance incidente sera réfléchie. Si vous utilisez plutôt une source de courant fixe, la réflexion due à la désadaptation d’impédance n’est pas prise en compte. Tout le courant traversera le matériau sous forme de courant de conduction ou de courant de déplacement, et seuls les courants de conduction entraîneront un échauffement.
En gardant à l’esprit ces équations et ces propriétés des matériaux, nous devrions désormais pouvoir comprendre pourquoi différentes conditions d’excitation entraînent différents niveaux de chauffage en fonction de la fréquence.
Excitation en tension
Nous allons maintenant nous intéresser à la condition Courants électriques, Terminal de type Tension. Cette condition aux limites a une signification claire en courant continu et à très basse fréquence, par exemple la tension d’une ligne 60 Hz dans les prises électriques domestiques. Cependant, à des fréquences plus élevées, nous devons réfléchir plus attentivement à la manière d’obtenir le même résultat à partir des interfaces Courants électriques et Ondes électromagnétiques.
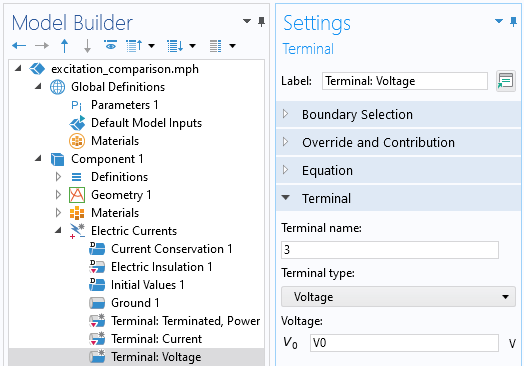
Vue de la condition Courants électriques, Terminal , de type Tension.
L’interface physique Ondes électromagnétiques ne dispose d’aucune condition aux limites directement équivalente à la fixation d’une tension sur toute une surface; vous pouvez uniquement définir le champ électrique à une frontière entre deux surfaces, ce qui n’a pas d’interprétation physique très claire à des fréquences élevées. Nous examinerons d’abord cette approche, puis nous présenterons une deuxième approche.
L’analogue le plus proche de la condition aux limites Courants électriques, Tension dans l’interface Ondes électromagnétiques est une condition Champ électrique, appliquée sur la même frontière annulaire que celle où le Port réduit était appliqué dans les approches précédentes. Dans cette condition aux limites Champ électrique, nous appliquons l’expression de la distribution du champ électrique qui conduira à la même différence de potentiel électrique à travers l’espace séparant les conducteurs. Pour un câble coaxial (aligné avec l’axe z), le champ électrique analytique à l’intérieur du diélectrique est
Cette expression est évaluée sur le maillage d’éléments finis et gagnera en précision avec le raffinement du maillage. Les paramètres de la condition aux limites et un exemple de maillage sont présentés dans la figure ci-dessous.
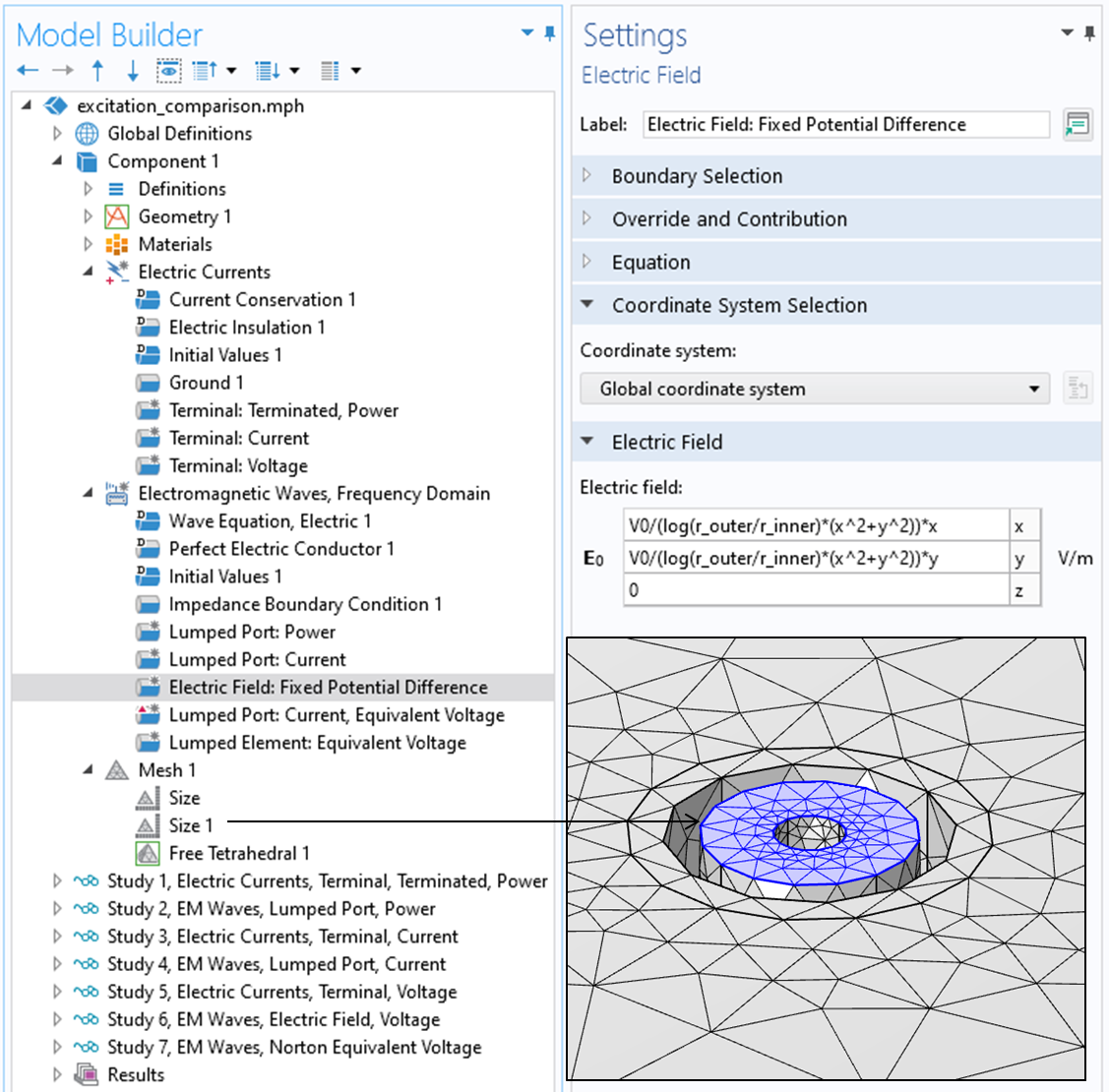
Vue de la condition aux limites Champ électrique dans l’interface Ondes électromagnétiques , ainsi qu’une visualisation du maillage.
Bien que cette approche, consistant à fixer le champ électrique dans l’interface physique Ondes électromagnétiques, soit la méthode analogue la plus directe à la condition Tension dans l’interface physique Courants électriques, elle est assez difficile à interpréter physiquement. Il peut donc être utile d’envisager d’autres alternatives.
Une approximation de la condition de tension peut également être mise en oeuvre en considérant l’équivalent Norton d’une source de tension et en utilisant un Port réduit, de type Courant, en parallèle avec un Elément réduit, d’une résistance relativement faible, placé à une courte distance le long du câble coaxial. Le courant imposé est ensuite ajusté de manière à ce que la chute de potentiel à travers l’élément réduit soit approximativement égale à la tension souhaitée.
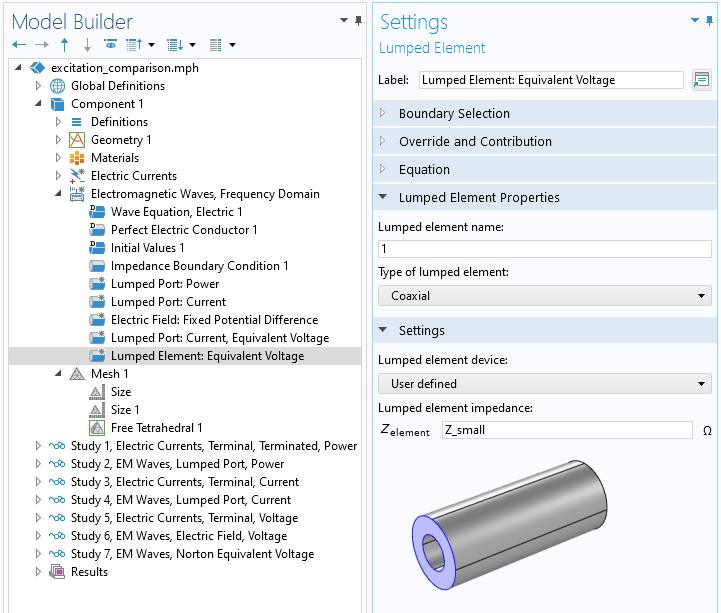
Vue de la condition aux limites Element réduit dans l’interface Ondes électromagnétiques.
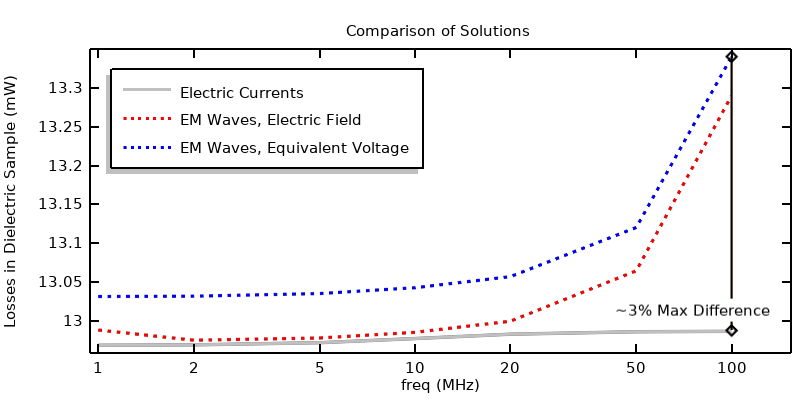
Comparaison des résultats obtenus en utilisant des excitations en tension.
Nous pouvons évaluer les pertes résultant des deux approches et les comparer, comme illustré dans la figure ci-dessus. Là encore, on observe une bonne concordance sur une large gamme de fréquences. Même à 100 MHz, la différence est inférieure à 3%. Nous pouvons également calculer les pertes à partir de l’impédance et de la tension de crête appliquées:
Remarque importante à propos de l’isolation
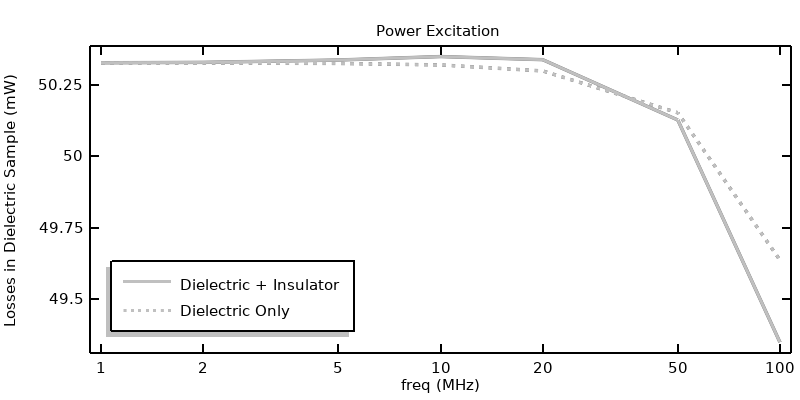
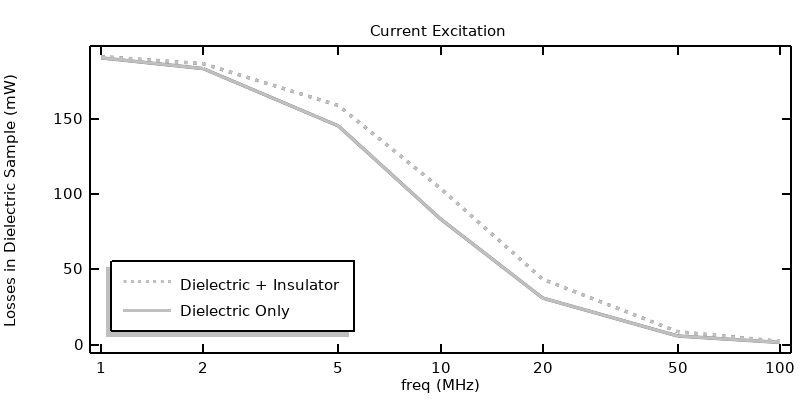
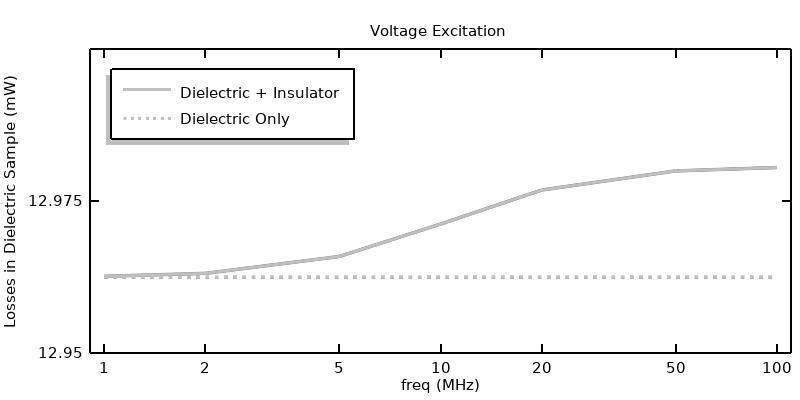
Dans l’article précédent, il a été observé que le matériau isolant à l’intérieur et autour des conducteurs coaxiaux pouvait être entièrement exclus du modèle Courants électriques dans le cas d’une excitation en puissance. Il est intéressant de vérifier cette observation pour tous les différents types d’excitation. Nous pouvons résoudre à nouveau toutes les approches précédentes, en résolvant les Courants électriques uniquement dans le diélectrique à pertes, puis comparer les résultats, comme montré dans la figure ci-dessous. Les excitations en puissance et en tension donnent des résultats très similaires, quelle que soit la modélisation de l’isolation. Cependant, pour une excitation en courant, les résultats sont significativement différents à des fréquences plus élevées, puisque le courant de déplacement n’est pas pris en compte dans le modèle.
Comparaison entre les pertes obtenues en résolvant les Courants électriques dans l’isolant et le diélectrique et celles obtenues en résolvant les Courants électriques dans le diélectrique seul. La différence est marquée pour une excitation en courant, mais négligeable pour une excitation en tension ou en puissance.
Connexion à l’interface physique Circuit électrique
Les conditions de source de tension et de courant que nous avons examinées jusqu’à présent sont idéalisées dans la mesure où nous ignorons toute structure intermédiaire entre notre source et notre système modélisé. Mais il arrive souvent que nous devions tenir compte d’une structure électrique importante. Nous pourrions inclure les détails exacts de ces structures dans le modèle, mais une approche simplifiée est également disponible via l’interface physique Circuit électrique, qui peut être combinée avec l’interface physique Courants électriques ou Ondes électromagnétiques.
À titre d’exemple, supposons que nous souhaitions modéliser un filtre simple, comme illustré dans le schéma ci-dessous. Une source de tension connectée à un condensateur, une inductance et une résistance en série avec le système, est modélisée. L’interface Circuit électrique repose sur le concept de noeuds, au niveau desquels le potentiel électrique est calculé. Le courant entre ces noeuds est déterminé en fonction de l’impédance de tout élément situé entre eux, ce qui peut correspondre à n’importe quelle fonctionnalité de l’interface Circuit électrique, ou être calculé à partir d’une autre interface physique via une fonctionnalité de Couplage externe. Dans cet exemple, nous voulons placer notre modèle entre les nœuds 3 et 4.
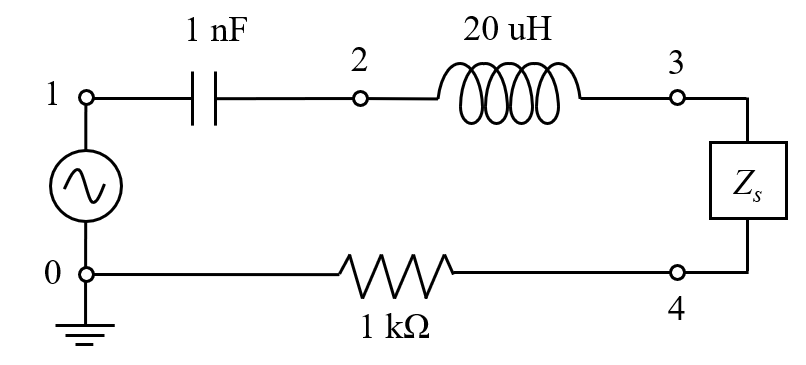
Schéma électrique d’une source de tension, d’un condensateur, d’un inducteur, et d’une résistance connectés au modèle du système.
Dans le contexte de la connexion d’un Circuit électrique à l’interface Courants électriques, le couplage est défini via la fonctionnalité I-terminal externe. Cela permet de coupler le potentiel électrique d’un nœud dans l’interface Circuit électrique avec le potentiel électrique d’un ensemble de surfaces dans l’interface Courants électriques, tel que défini via la condition aux limites Terminal de type Circuit. Avec cette approche, il ne devrait y avoir qu’une seule condition de masse dans le modèle, et celle-ci devrait se trouver dans l’interface Circuit électrique.
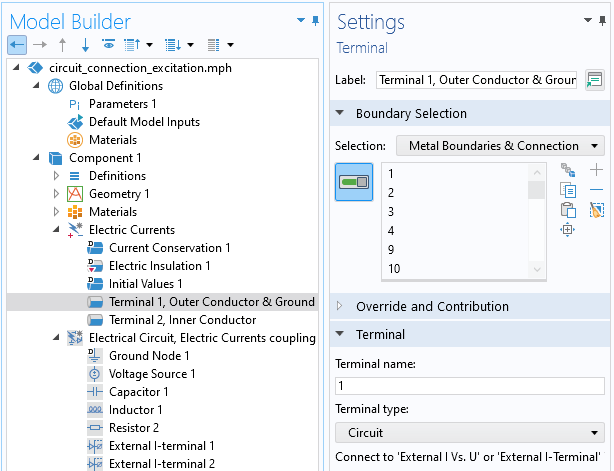
La condition Terminal de type Circuit. Le potentiel électrique des surfaces sélectionnées du terminal sera couplé à un noeud du Circuit électrique.
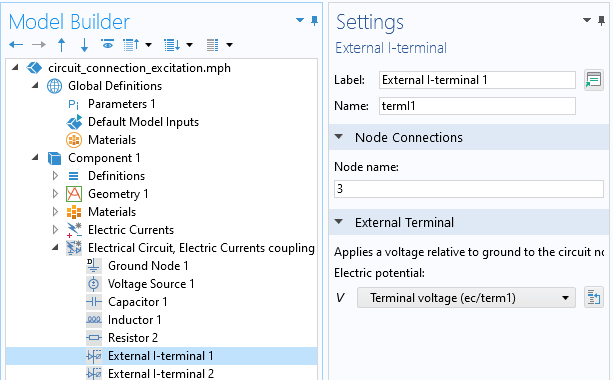
La fonctionnalité I-terminal externe spécifie le couplage entre le noeud du Circuit électrique et le potentiel électrique du Terminal .
Dans le contexte de la connexion d’un Circuit électrique avec une interface Ondes électromagnétiques, le couplage est défini via la fonctionnalité I vs. U externe. Cela permet de coupler la différence de potentiel électrique entre deux nœuds du Circuit électrique à la différence de potentiel électrique à travers un Port réduit, de type Circuit, dans l’interface Ondes électromagnétiques.
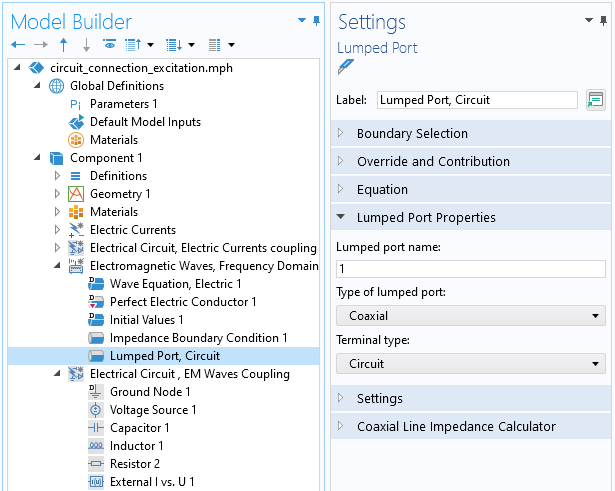
La condition Port réduit de type Circuit. La différence de potentiel électrique sera couplée avec la différence de potentiel entre deux noeuds de l’interface Circuit électrique.
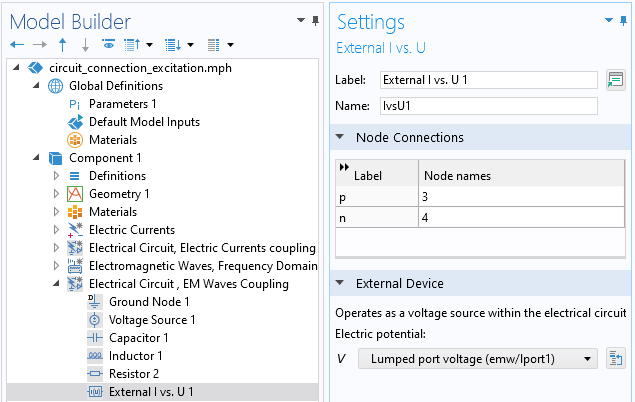
La fonctionnalité I vs. U externe couple la différence de potentiel du Port réduit entre deux noeuds du Circuit électrique.
L’ajout de l’interface Circuit électrique entraîne un coût de calcul supplémentaire, car elle nécessite souvent l’utilisation du solveur Direct pour calculer le système d’équations entièrement couplé (voir également notre article de la Base de connaissances “Understanding the Fully Coupled vs. Segregated approach and Direct vs. Iterative linear solvers”). Cela augmente les besoins en mémoire et le temps de calcul. Les résultats sont présentés dans la figure ci-dessous, et la différence entre les deux approches est négligeable. Notez que le pic dans les pertes en fonction de la fréquence est dû à l’inducteur réduit.
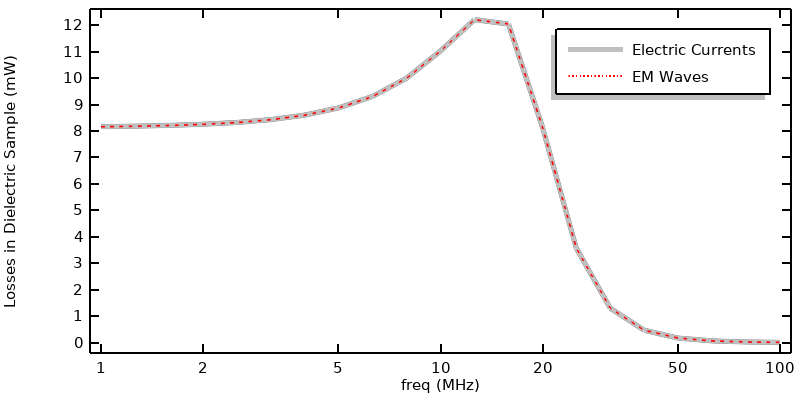
Pertes en fonction de la fréquence lorsqu’un condensateur, un inducteur, et une résistance sont placés en série entre la source de tension et le modèle.
Dépôt d’une puissance fixe dans le modèle
Enfin, supposons que vous souhaitiez modéliser une source qui comprend une boucle de rétroaction qui ajuste l’entrée de manière à ce qu’une puissance fixe soit déposée. Il existe plusieurs façons d’y parvenir. Nous commencerons par mentionner brièvement les deux options intégrées et discuterons de leurs limites, puis nous présenterons une troisième approche, plus générale, qui nécessite davantage de configuration mais offre plus de flexibilité.
Dans la condition aux limites Courants électriques, terminal, l’option Puissance implémente la rétroaction en introduisant une équation de couplage supplémentaire dans le modèle qui ajustera le courant appliqué de manière à ce que la puissance crête-à-crête spécifiée soit déposée dans le modèle. Autrement dit, quelle que soit la puissance spécifiée dans le terminal, elle sera deux fois supérieure à la puissance dissipée dans le domaine, pour un modèle dans le domaine fréquentiel. Cette équation supplémentaire entièrement couplée donne lieu à un système d’équations qui est non linéaire et asymétrique, ce qui signifie que la convergence dépend des valeurs initiales, de la mise à l’échelle et des paramètres du solveur, et nécessite un solveur direct entièrement couplé. Elle sera donc coûteuse en termes de calcul et doit être réservée uniquement aux cas où le modèle présente une très forte non-linéarité, comme pour la modélisation du plasma.
Dans l’interface physique Ondes électromagnétiques, il existe la condition aux limites Port, avec l’option Permettre le retour du port actif. La condition aux limites Port peut être utilisée pour tout type de guide d’ondes ou de ligne de transmission. Cette condition aux limites est moins exigeante en termes de calcul. Cependant, ces deux approches présentent un inconvénient: elles déposent la puissance spécifiée dans l’ensemble du modèle, sur tous les domaines et toutes les conditions aux limites, ce qui peut entraîner des pertes.
Supposons que nous souhaitions plutôt spécifier la puissance déposée dans un seul domaine (ou limite) du modèle. Dans ce cas, nous devons utiliser une approche différente, en introduisant une Equation globale qui ajuste de manière itérative la donnée d’entrée afin d’obtenir la sortie idéale, comme décrit ici.
En résumé, cette approche se compose de trois étapes, quelle que soit la physique à résoudre:
- Spécifier l’excitation à l’aide d’une variable définie via une Equation globale.
- Ecrire une expression de mise à jour pour l’Equation globale qui mettra à jour de manière itérative l’amplitude de l’excitation au cours de la résolution.
- Vérifier que le solveur ségrégé est utilisé afin que l’Equation globale soit résolue dans une étape distincte.
Nous examinerons en détail le cas d’une excitation en courant appliquée aux Courants électriques, les autres cas étant assez similaires dans leur configuration.
Pour commencer, le courant appliqué n’est pas spécifié comme une constante, mais via une variable, comme le montre la capture d’écran ci-dessous:
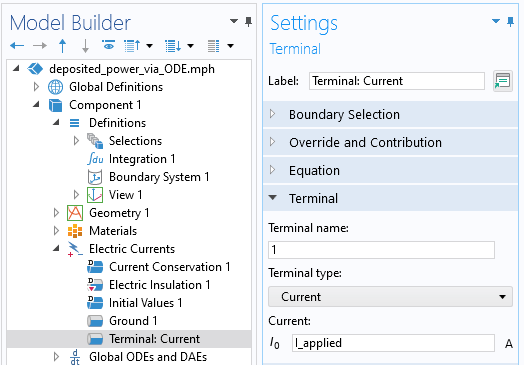
Une capture d’écran montrant le courant spécifié par une variable.
Ensuite, l’équation de mise à jour pour le courant appliqué est spécifiée à travers l’interface Equations globales, comme montré dans la capture d’écran ci-dessous.
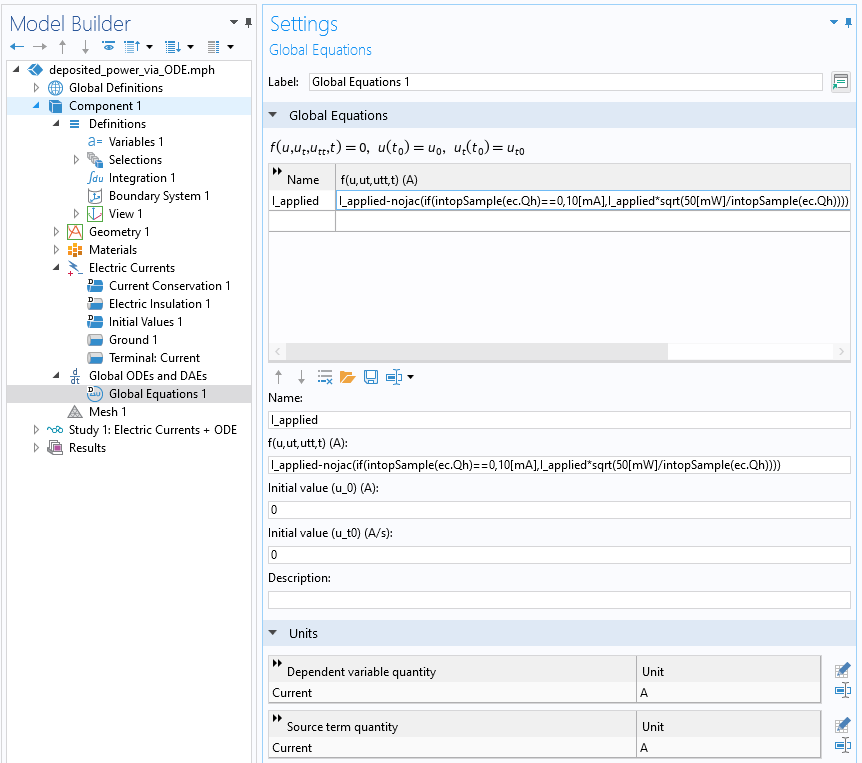
Implémentation d’une équation de rétroaction via une Equation globale supplémentaire. Notez que les unités sont définies en ampères.
L’équation de mise à jour itérative est la suivante:
I_applied-nojac(if(intopSample(ec.Qh)==0,10[mA],I_applied*sqrt(50[mW]/intopSample(ec.Qh)))).
Cette équation utilise un couplage d’intégration appelé intopSample() qui calcule l’intégrale des pertes dans le domaine choisi. Cette équation vérifie d’abord si la perte intégrée est nulle (état initial) et, si c’est le cas, elle définit le courant à 10 mA. Sinon, elle compare la dissipation calculée à la dissipation cible de 50 mW et ajuste le courant appliqué. Cette expression contient donc à la fois l’initialisation du courant et l’expression de mise à jour. Il est donc nécessaire de s’assurer que le solveur ségrégé est utilisé et que la variable de l’interface EDO et EAD globales est résolue en premier, comme le montre la capture d’écran ci-dessous. La deuxième étape ségrégée, qui consiste à résoudre les Courants électriques, peut alors utiliser le solveur itératif plus efficace en termes de calcul.
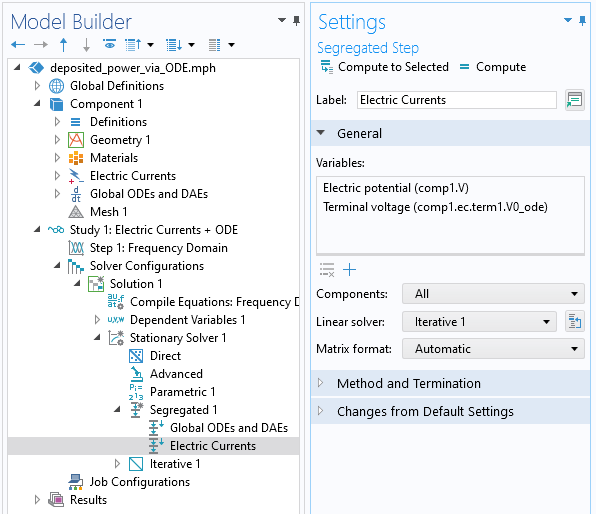
Les réglages du solveur ségrégé. L’équation d’initialisation et de rétroaction est d’abord résolue, puis les équations physiques sont résolues par défaut à l’aide du solveur itératif.
Avec cette approche, les pertes dans l’échantillon diélectrique seront de 50 mW à toutes les fréquences, et nous pouvons tracer le courant appliqué, ou la tension appliquée, qui permettra d’atteindre cette dissipation.
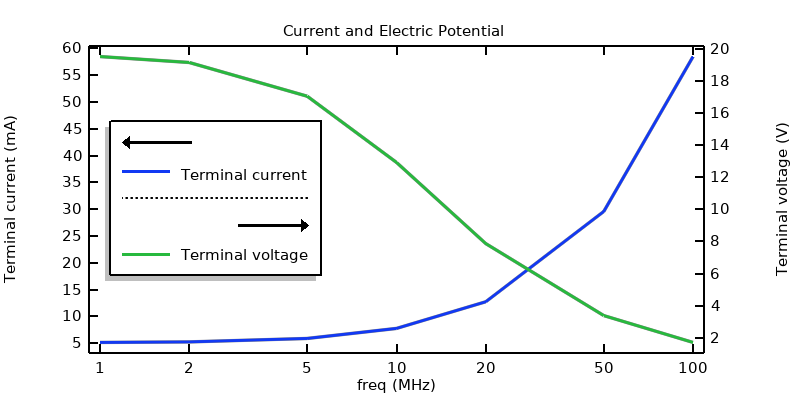
Le courant et la tension du terminal qui entraineront une dissipation dans le domaine choisi.
Conclusion
Nous avons passé en revue les types d’excitation utilisés pour la modélisation des courants électriques dans le domaine fréquentiel et les avons comparés à leurs équivalents dans l’interface physique Ondes électromagnétiques. Nous nous sommes concentrés ici sur la plage de fréquences 1–100 MHz pour ce système, mais selon le cas, les conclusions peuvent s’étendre en dessous ou même au-delà de cette plage. Ce qu’il faut retenir ici, c’est la compréhension des différences entre les options d’excitation et leur utilisation. Les fichiers associés sont disponibles via le bouton ci-dessous.







Commentaires (0)