Analyser le modèle de Hodgkin-Huxley à l’aide d’une application de simulation

Dans un précédent article de blog, nous avons abordé les bases physiologiques de la génération du potentiel d’action dans les cellules excitables des organismes vivants. Nous avons présenté le modèle simple de Fitzhugh-Nagumo, qui émule le processus de dépolarisation et de repolarisation dans le potentiel membranaire d’une cellule. Aujourd’hui, nous analysons un modèle plus avancé pour simuler le potentiel d’action, le modèle de Hodgkin-Huxley. Nous abordons également l’utilisation d’une application de simulation pour rationaliser ce type d’analyse.

Explorer le potentiel d’action dans les cellules à l’aide du modèle de Hodgkin-Huxley

Nous avons déjà abordé les bases physiques du mécanisme de déclenchement qui génère le potentiel d’action dans les cellules et nous avons étudié la génération d’une telle forme d’onde à l’aide du modèle de Fitzhugh-Nagumo.

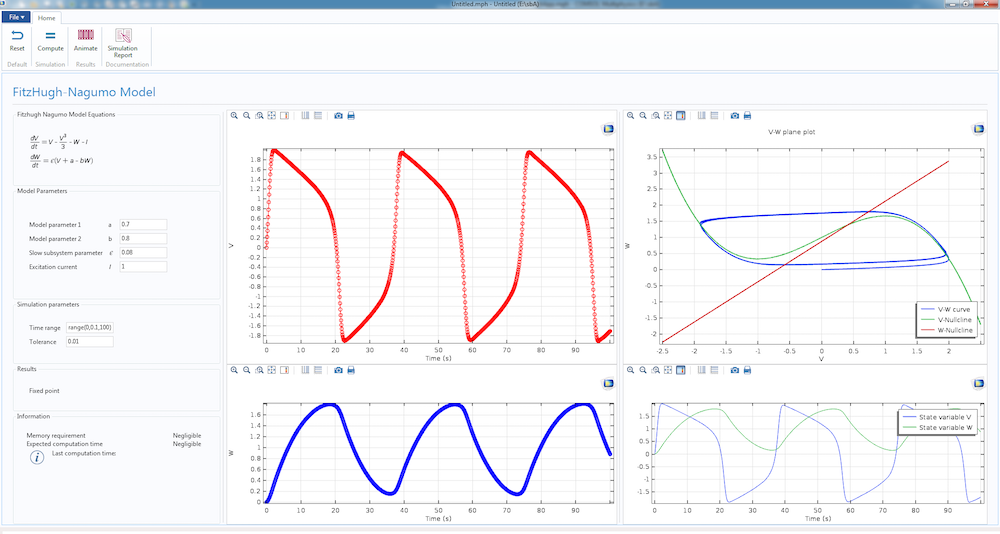
La dynamique du modèle simple de Fitzhugh-Nagumo, présentée dans une application de simulation.

Nous allons maintenant convertir l’étude du modèle de Fitzhugh-Nagumo (FH) en un modèle mathématique plus rigoureux, le modèle de Hodgkin-Huxley (HH). Contrairement au modèle FH, qui fonctionne bien comme preuve de concept, le modèle HH est basé sur la physiologie cellulaire et les résultats de la simulation correspondent bien aux expériences.

Dans le modèle HH, la membrane cellulaire contient des canaux activés et non activés qui permettent le passage des ions. Les canaux non activés sont toujours ouverts, tandis que les canaux activés s’ouvrent dans des conditions particulières. Lorsque la cellule est au repos, les neurones permettent le passage des ions sodium et potassium à travers les canaux non activés. Supposons tout d’abord que seuls les canaux potassiques existent. Pour le potassium, qui est en excès à l’intérieur de la cellule, la différence de concentration entre l’intérieur et l’extérieur de la cellule agit comme une force motrice pour le déplacement des ions. Il s’agit du processus de mouvement des ions par diffusion, ou du mécanisme chimique qui expulse initialement le potassium hors des cellules.

Ce processus de diffusion ne peut pas se poursuivre indéfiniment. En effet, les ions potassium sont chargés. Une fois qu’ils s’accumulent à l’extérieur de la cellule, ces ions établissent un gradient électrique qui pousse certains ions potassium à pénétrer dans les cellules. Il s’agit du deuxième mécanisme (le mécanisme électrique) qui influence le mouvement des ions. Finalement, ces deux mécanismes se compensent et les deux flux de potassium s’équilibrent. Le potentiel auquel cet équilibre se produit est appelé potentiel de Nernst pour cet ion. Dans les cellules excitables, la valeur du potentiel de Nernst pour le potassium, E_{K}, est de -77 mV. Pour les ions sodium, E_{Na}, elle est d’environ 50 mV.

Nous autorisons la présence de quelques canaux sodiques non activés dans la membrane. Les ions sodium étant abondants dans la région extracellulaire, un afflux d’ions sodium dans la cellule doit se produire. Les ions sodium entrants réduisent le gradient électrique, perturbent l’équilibre potassique et entraînent un efflux net de potassium hors de la cellule jusqu’à ce que celle-ci atteigne son potentiel de repos, à environ -70 mV. Il est important de mentionner ici que l’efflux net de potassium et l’afflux net d’ions sodium ne peuvent pas se poursuivre indéfiniment, sinon le gradient chimique qui provoque le mouvement finira par cesser. Les pompes à ions ramènent le potassium dans la cellule et expulsent le sodium par transport actif, maintenant ainsi le potentiel de repos des cellules dans des conditions normales.

Nous allons construire un modèle de circuit équivalent d’une cellule dans lequel nous pouvons imiter les effets des différents mécanismes cellulaires que nous venons de décrire à l’aide de différents composants de circuit courants, tels que des condensateurs, des résistances et des batteries. La réponse en tension du circuit est le signal qui correspond au potentiel d’action.

On peut distinguer quatre courants importants pour le modèle HH :

1. Le courant qui circule dans la membrane cellulaire
2. Un courant sodique
3. Un courant potassique
4. Un courant de fuite qui tient compte de tout autre courant, à l’exception des trois premiers

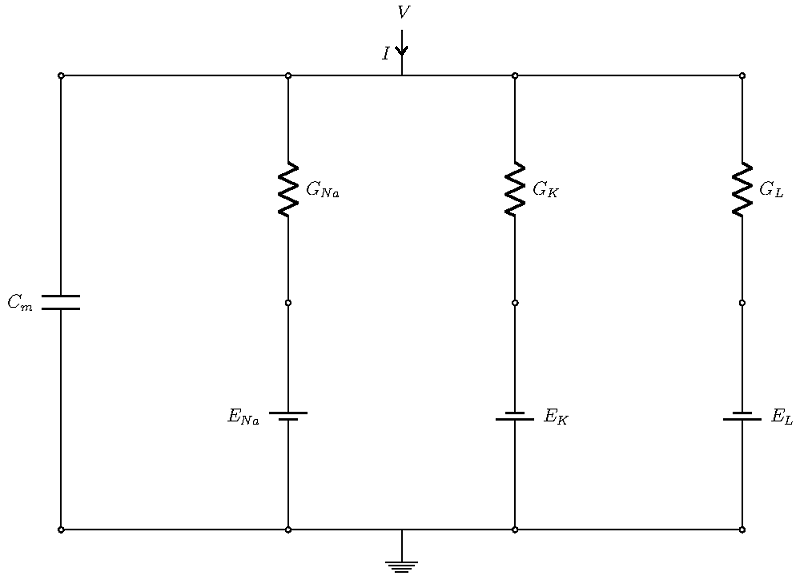
Schéma des courants dans un modèle de Hodgkin-Huxley.

Les quatre courants circulent à travers des branches parallèles, avec le potentiel membranaire V comme force motrice (voir la figure ci-dessus ; la masse représente le potentiel extracellulaire). La membrane cellulaire a un comportement capacitif, ce qui lui permet de stocker une charge. Dans la figure ci-dessus, il s’agit de la branche la plus à gauche, modélisée avec un condensateur de force C_m. Les autres branches correspondent à trois courants ioniques qui circulent à travers les canaux ioniques. Dans chaque branche, les effets des canaux sont modélisés par la conductance (représentée par la résistance dans le diagramme), et l’effet du gradient de concentration est représenté par le potentiel de Nernst des ions, qui sont représentés par des piles.

Ainsi, lorsqu’un courant est injecté dans la cellule, il est divisé en quatre parties et la conservation des charges nous conduit à l’équation d’équilibre suivante

Ou de manière équivalente

Ce qui est primordial, c’est que les conductances des canaux sodiques et potassiques ne sont pas constantes ; elles dépendent du potentiel cellulaire. Comment les modéliser ? Rappelons-nous que certains canaux ioniques sont activés et peuvent avoir plusieurs portes. Supposons qu’il existe des fonctions de vitesse dépendant de la tension α_p (V) et β_p (V), qui nous donnent respectivement les constantes de vitesse d’une porte passant d’un état fermé à un état ouvert et d’un état ouvert à un état fermé. Si p désigne la fraction de portes ouvertes, une simple loi d’équilibre donne l’équation suivante pour l’évolution de p

Les différents canaux ioniques sont caractérisés par leurs portes. Dans le modèle HH, on suppose que le canal potassique est composé de quatre portes de type n. Étant donné que le canal est conducteur lorsque les quatre portes sont ouvertes, la conductance potassique est modélisée à l’aide de l’équation suivante

Pour le sodium, la situation est supposée plus complexe. Le canal sodique comporte quatre portes, mais trois portes de type-m (portes de type activation qui s’ouvrent lorsque la cellule se dépolarise) et une porte de type-h (porte de désactivation qui se ferme lorsque la cellule se dépolarise). Par conséquent, la conductance du canal sodique est donnée par

Dans les équations ci-dessus, \bar{g}_{K} et \bar{g}_{Na} correspondent à la conductance maximale du potassium et du sodium. Les formes fonctionnelles de α_p (V), β_p (V) pour p =m, n, h peuvent être trouvées dans les ouvrages de référence.

La conductance de fuite est supposée constante. Par conséquent, le modèle HH est entièrement décrit par l’ensemble d’équations suivant

Comprendre la dynamique du modèle HH grâce à la simulation

La clé pour comprendre le modèle de Hodgkin-Huxley réside dans la compréhension des équations des portes. Nous pouvons reformuler les équations des portes de la façon suivante

avec p_{\infty}\left(V\right) = \frac{\alpha_p\left(V\right)}{\alpha_p\left(V\right) + \beta_p\left(V\right)}, \quad \tau_p\left(V\right) = \frac{1}{\alpha_p\left(V\right) + \beta_p\left(V\right)}.

Il s’agit d’une équation très connue dans les circuits électriques. Si nous supposons que p_∞ est indépendant de la tension, alors l’équation indique que p tend asymptotiquement vers p_∞ comme valeur finale, et que τ_p, la constante de temps, détermine la vitesse à laquelle la convergence s’opère. Cela signifie que plus τ_p est petite, plus la convergence est rapide. La figure suivante montre les valeurs de ces deux quantités pour p =m, n, h.

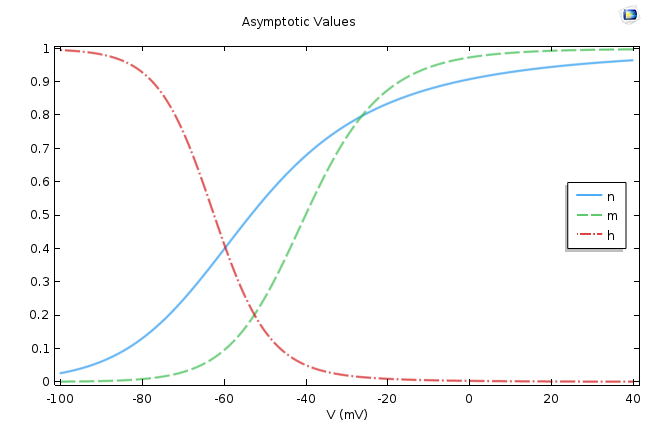
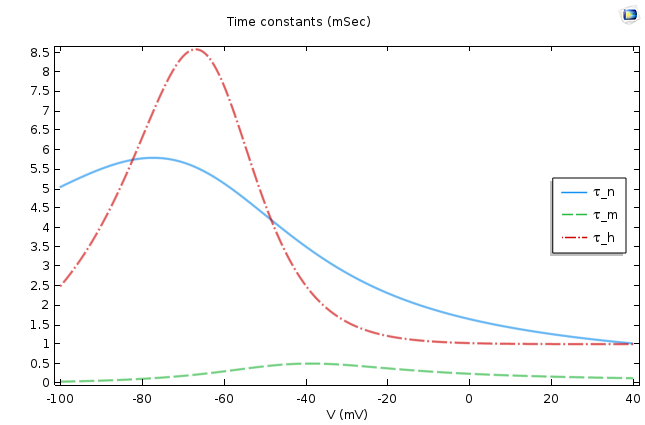
Les valeurs asymptotiques (à gauche) et les constantes de temps (à droite) pour les équations de porte du modèle de Hodgkin-Huxley.

Il est facile de conclure à partir des figures ci-dessus que n_∞ et m_∞ augmentent à mesure que la cellule se dépolarise et que h_∞ diminue dans des conditions similaires. À partir du deuxième graphique, nous constatons que l’activation du sodium est beaucoup plus rapide que celle du potassium ou du courant de fuite.

Lorsque la dépolarisation commence, n_∞ et m_∞ augmentent, et h_∞ diminue. Les équations qui régissent toutes ces quantités imposent qu’elles se rapprochent des valeurs d’équilibre ; par conséquent, n et m augmentent et h diminue. Cependant, il faut également tenir compte des différences entre les constantes de temps des variables de porte. Une comparaison montre que l’activation des canaux sodiques est beaucoup plus rapide que leur désactivation ou l’ouverture des canaux potassiques. Il en résulte donc une augmentation globale initiale de la conductance sodique. Cela entraîne une augmentation du courant sodique, qui élève le potentiel membranaire et fait tendre V vers E_{Na}. C’est ainsi que le modèle HH explique la partie ascendante du potentiel d’action.

Cependant, à mesure que ce processus se poursuit, h \rightarrow 0. Une fois que la valeur de h passe en dessous d’un seuil, les canaux sodiques sont effectivement fermés. De plus, à mesure que V tend vers E_{Na}, la force motrive du courant sodique diminue. Pendant ce temps, les canaux potassiques, qui ont une constante de temps plus lente, s’ouvrent de manière importante. Ceci, associé à la force motrice élevée V-E_{k} disponible pour le courant potassique, force le flux inverse. Les ions potassiques sortent de la cellule et le potentiel membranaire finit par se stabiliser vers l’état hyperpolarisé.

Création et utilisation d’une application de simulation pour analyser le modèle de Hodgkin-Huxley

Nous pouvons créer une application de simulation pour analyser le modèle de Hodgkin-Huxley, ce qui nous permet de tester différents paramètres sans modifier le modèle complexe sous-jacent. Pour ce faire, nous pouvons concevoir une interface utilisateur conviviale à l’aide du Constructeur d’applications du logiciel COMSOL Multiphysics®. Dans un premier temps, nous créons un modèle basé sur les équations de Hodgkin-Huxley à l’aide du Constructeur de modèles du logiciel COMSOL. Une fois le modèle construit, nous le transformons en application à l’aide du Constructeur d’applications. En créant une application, nous pouvons sélectionner et contrôler les différentes entrées et sorties de notre modèle. Nous transmettons ensuite l’application à l’utilisateur final, qui n’a pas à se soucier du processus de configuration du modèle et peut se concentrer sur l’extraction et l’analyse des résultats de la simulation.

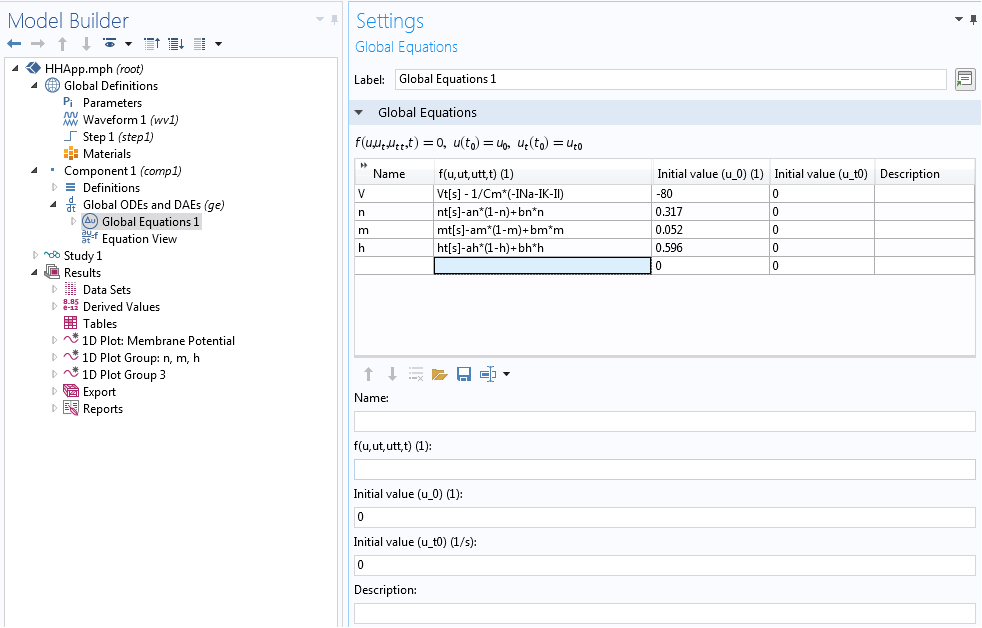
Dans le cas présent, nous avons implémenté le modèle de Hodgkin-Huxley à l’aide de l’interface EDO et EAD globales dans COMSOL Multiphysics. Cette interface fait partie des fonctionnalités mathématiques du logiciel COMSOL et permet de résoudre un système d’équations différentielles ordinaires et différentielles algébriques. Cette interface est souvent utilisée pour construire des modèles dont les équations et les conditions aux limites initiales sont génériques. Dans l’interface, nous pouvons spécifier les équations et les inconnues et ajouter des conditions initiales. L’interface, avec les équations du modèle, est illustrée ci-dessous.

Nous créons également les éléments permettant d’exploiter les résultats, les graphiques et les animations dans le Constructeur de modèles. Une fois le modèle prêt, nous revenons dans l’interface du Constructeur d’applications. Nous connectons les éléments du modèle à l’interface utilisateur de l’application à l’aide de diverses options telles que des champs de saisie, des boutons de commande, des panneaux d’affichage et la programmation de méthodes de modèles.

Vous pouvez en apprendre plus sur la création et l’exécution d’applications de simulation dans ce webinaire archivé.

Enfin, nous pouvons concevoir l’interface utilisateur de l’application de Hodgkin-Huxley. Grâce à l’Editeur de formulaires du Constructeur d’applications, nous pouvons concevoir une interface utilisateur personnalisée avec différents boutons, panneaux et affichages. Cette interface utilisateur comprend une section Paramètres du modèle permettant de saisir les différents paramètres du modèle HH, tels que le potentiel de Nernst, la conductance maximale de la porte et la capacité membranaire. Nous pouvons également fournir deux types de courant d’excitation au modèle : un courant à échelon unitaire ou un train d’excitation. À mesure que les paramètres changent, l’application affiche le potentiel d’action et le courant d’excitation, ainsi que l’évolution des variables de porte m, n et h.

Grâce aux boutons Réinitialiser et Calculer, il est facile d’effectuer plusieurs tests après avoir modifié les paramètres. Des panneaux graphiques permettent également de visualiser et tracer les résultats du modèle. Le bouton Rapport génère un résumé de la simulation.

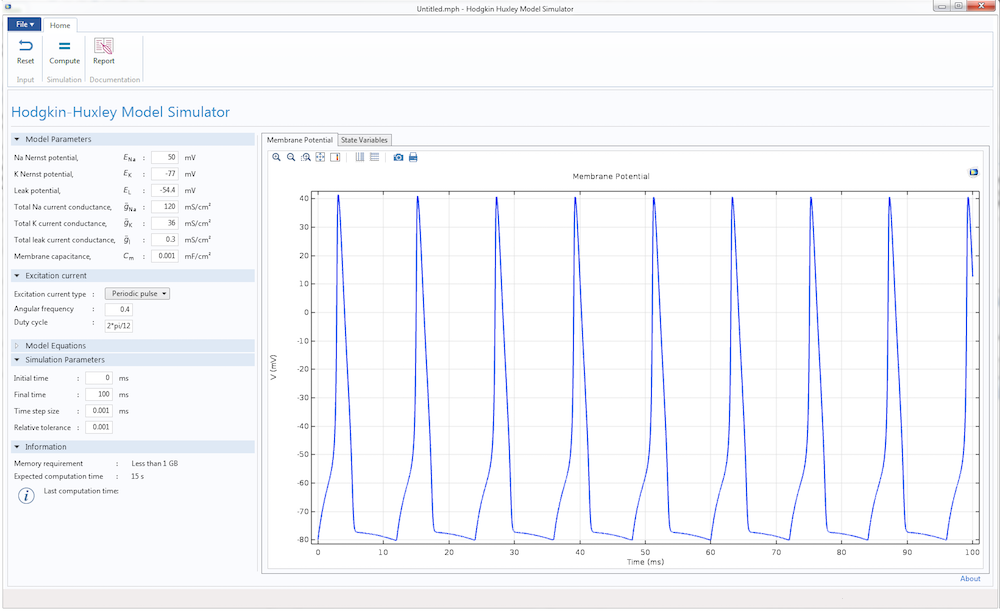
Interface utilisateur de l’application de simulation du modèle de Hodgkin-Huxley.

La mise en place de boutons dans une application est un processus simple. Il suffit d’écrire quelques méthodes à l’aide de l’outil Éditeur de méthodes disponible dans le Constructeur d’applications, puis de les associer correctement aux boutons. Illustrons comment cela fonctionne à l’aide d’un exemple. Nous pouvons concevoir l’application du modèle de Hodgkin-Huxley de manière à ce que, lors de son lancement, le bouton Rapport soit inactif (voir la figure ci-dessous). En effet, l’utilisateur de l’application n’aura besoin d’utiliser ce bouton qu’après avoir effectué une simulation.

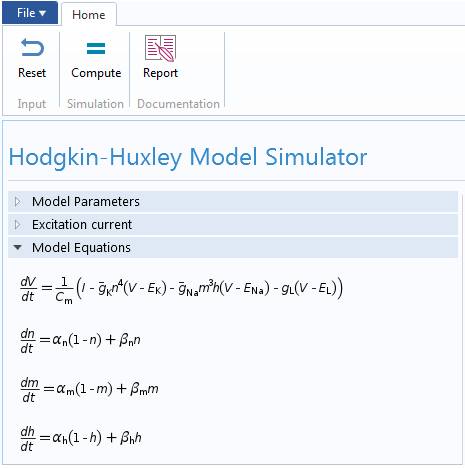
Le bouton Rapport est désactivé au début de la simulation.

Pour ce faire, nous pouvons écrire une méthode qui demande à l’application d’exécuter certaines fonctions lors du lancement de l’application.

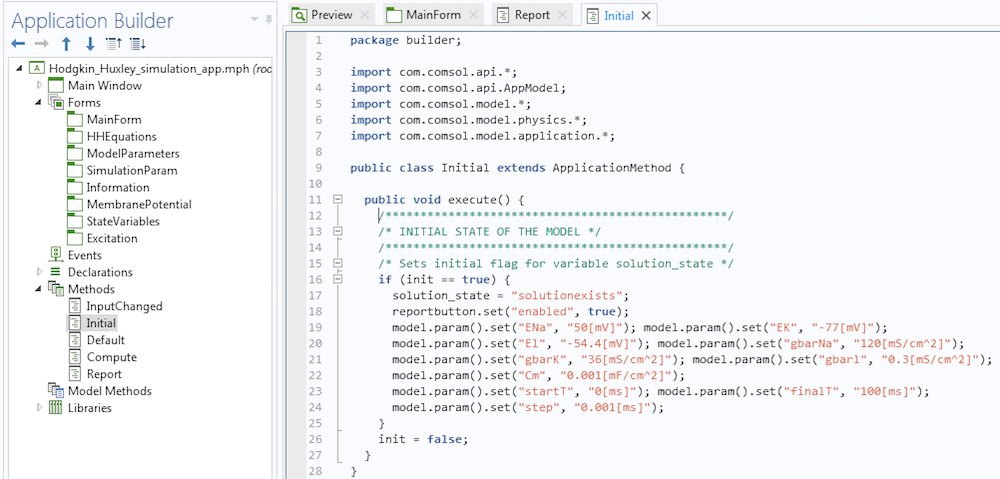
Une méthode qui désactive le bouton Rapport lors du lancement de l’application.

Notez que nous avons désactivé le bouton Rapport en suivant les instructions des lignes 7 et 8 de la méthode. Si vous vous inquiétez de la syntaxe à utiliser pour vos méthodes, je vous assure qu’elle est beaucoup plus simple qu’il n’y paraît. Tout d’abord, les méthodes exécutent certaines actions. Si nous voulons enregistrer le code correspondant à ces actions, nous cliquons sur le bouton Enregistrer la méthode dans le ruban du Constructeur d’applications. Ensuite, nous pouvons revenir dans le Constructeur de modèles, exécuter les actions souhaitées, puis cliquer sur le bouton Arrêter l’enregistrement. Le code correspondant sera placé dans la méthode. Si nécessaire, nous pouvons ensuite modifier les instructions.

Une fois la simulation terminée, nous souhaitons que ce bouton devienne actif dans l’application. Dans une autre méthode associée au bouton Calculer, nous insérons le segment de code suivant

Nous nous assurons ensuite que ce segment est exécuté si la solution est calculée avec succès. Vous verrez que cela active le bouton.

En résumé, vous pouvez utiliser une application de simulation pour calculer et visualiser facilement les changements de paramètres lorsque vous travaillez avec un modèle complexe impliquant plusieurs équations et types de physique, tel que le modèle de Hodgkin-Huxley présenté ici. Cette application de simulation n’est qu’un exemple parmi d’autres de la manière dont vous pouvez concevoir la structure d’une application et personnaliser ses paramètres d’entrée en fonction de vos besoins. Utilisez cette application comme source d’inspiration pour créer votre propre application, que ce soit pour analyser le potentiel d’action dans une cellule à l’aide d’un modèle mathématique ou pour enseigner à vos élèves des concepts mathématiques et d’ingénierie complexes. Quel que soit l’objectif de votre application, elle garantira que votre processus de simulation est simple et intuitif.

Ressources complémentaires

• Sur le blog COMSOL :
  • Lisez un précédent article de blog explorant la dynamique du modèle de Fitzhugh-Nagumo à l’aide d’une application de simulation
  • En savoir plus sur l’utilisation des applications de simulation pour rationaliser votre processus de modélisation
• Parcourez les webinaires en direct à venir pour en savoir plus sur les fonctionnalités de COMSOL Multiphysics