La Bibliothèque d'Applications présente des modèles construits avec COMSOL Multiphysics pour la simulation d'une grande variété d'applications, dans les domaines de l'électromagnétisme, de la mécanique des solides, de la mécanique des fluides et de la chimie. Vous pouvez télécharger ces modèles résolus avec leur documentation détaillée, comprenant les instructions de construction pas-à-pas, et vous en servir comme point de départ de votre travail de simulation. Utilisez l'outil de recherche rapide pour trouver les modèles et applications correspondant à votre domaine d'intérêt. Notez que de nombreux exemples présentés ici sont également accessibles via la Bibliothèques d'Applications intégrée au logiciel COMSOL Multiphysics® et disponible à partir du menu Fichier.
This model uses the discrete-ordinates method (DOM) to analyze the radiative heat transfer in a utility boiler with internal obstacles. DOM is one of the most useful radiation models for prediction of radiative heat fluxes on the furnace walls of a combustion chamber. With this model, ... En savoir plus
This example reproduces parts of the study of Ref. 1 on the thermal contact resistance at the interface between a heat sink and an electronic package. Eight cooling fins equip the cylindrical heat sink and contact is made at the radial boundaries of the package. The efficiency of the ... En savoir plus
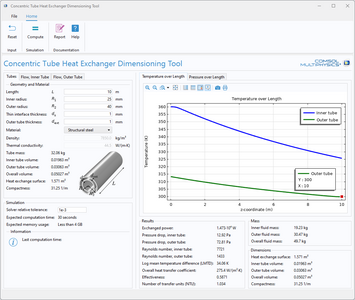
This model solves the fluid flow and heat transfer in a micro heat exchanger made of stainless steel. These types of heat exchangers are found in lab-on-chip devices in biotechnology and micro reactors, for example for micro fuel cells. The model takes heat transferred through both ... En savoir plus
The heat transfer rate and hydraulic resistance of a three dimensional heat exchanger is optimized in the laminar flow regime. En savoir plus
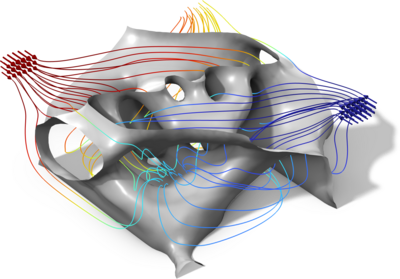
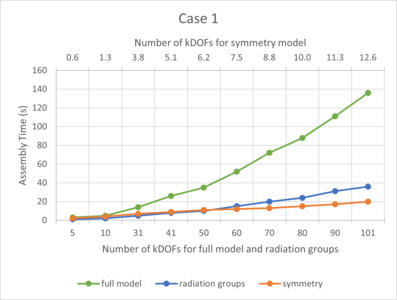
This model shows how to use the features of the Heat Transfer Module to reduce the computation time and memory usage in view factor computations. Illustrative results of speedup and memory usage reduction are given on a benchmark model. The solution is not computed, only the view ... En savoir plus
This app demonstrates the following: Selecting predefined or user-defined materials User option to switch between laminar flow or turbulent flow Changing boundary conditions using methods Visualizing temperature dependent material properties as graph plots User option to set the solver ... En savoir plus
This example describes the cooling and solidification, from melt to solid metal, in a continuous casting process. The model includes nonisothermal properties, temperature distribution, flow field, and phase change. This example uses the arbritrary Lagrangian-Eulerian method for modeling ... En savoir plus
In friction stir welding, a rotating tool moves along the weld joint and melts the aluminum through the generation of friction heat. The tool’s rotation stirs the melted aluminum such that the two plates are joined. In this model, two aluminum plates are joined by generating friction ... En savoir plus
This 2D stationary model computes heat and moisture transport in a wall composed of different hygroscopic materials. A comparison with the Glaser method is given for the temperature and relative humidity solutions. The effect of the use of a vapor barrier is also investigated. En savoir plus
When cooking food, such as a patty, in convection ovens there is a trade off in the heating method. If the patty is heated at a low oven temperature the cooking is slow and the patty dries out, resulting in a poor taste. If the patty is heated rapidly at a high temperature, it is ... En savoir plus