Derniers Articles
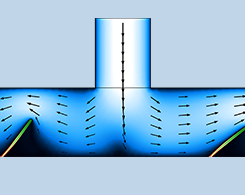
Simuler les mécanismes d’une micropompe sans clapet
Les micropompes sans clapet sont intégrées dans de nombreux systèmes microfluidiques. La simulation peut être utilisée pour étudier l’interaction fluide-structure ayant lieu dans ces composants afin d’améliorer leurs performances.

Modéliser les non-idéalités en spectroscopie d’impédance électrochimique
Dans cet article de blog, nous explorons comment modéliser les non-idéalités en spectroscopie d’impédance électrochimique (EIS), souvent utilisée dans l’étude des systèmes électrochimiques.

Optimiser le procédé CVD avec COMSOL Multiphysics®
Le dépôt chimique en phase vapeur est utilisé dans presque tous les procédés de fabrication de semi-conducteurs. La modélisation et la simulation multiphysiques se révèlent être des outils incontournables pour mieux comprendre ce procédé.
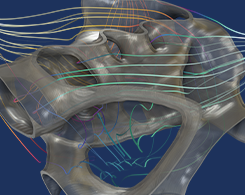
Optimisation des échangeurs de chaleur
Le développement d’échangeurs de chaleur est une tâche délicate en raison de leurs coûts de conception et de fabrication. Découvrez comment l’optimisation de forme et l’optimisation topologique peuvent vous y aider.

Utiliser la fenêtre Chatbot dans COMSOL Multiphysics®
La version 6.3 de COMSOL Multiphysics® a introduit une fenêtre Chatbot. Découvrez quelques exemples montrant comment cette fonctionnalité peut se révéler être un assistant précieux pour toutes vos modélisation.

Modéliser l’écoulement sanguin dans la sténose d’une artère pulmonaire
L’écoulement sanguin à travers une artère pulmonaire sténosée peut être modélisé en représentant la sténose comme un milieu poreux. Découvrez comment dans cet article de blog.

Introduction à l’interface Transport d’électrolyte concentré
La version 6.3 de COMSOL® introduit une nouvelle interface, permettant la modélisation d’électrolytes contenant un nombre arbitraire d’espèces électrolytiques. Pour en savoir plus, cliquez ici.
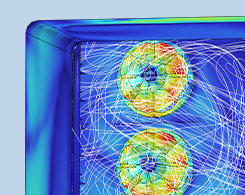
5 exemples concrets de modélisation et de simulation pour la sécurité alimentaire
La confiance des consommateurs au sujet de la sécurité alimentaire a atteint un niveau historiquement bas en 2024, d’où l’importance pour les entreprises de garantir la sûreté de leurs produits. La modélisation et la simulation sont des outils qui œuvrent en ce sens.
