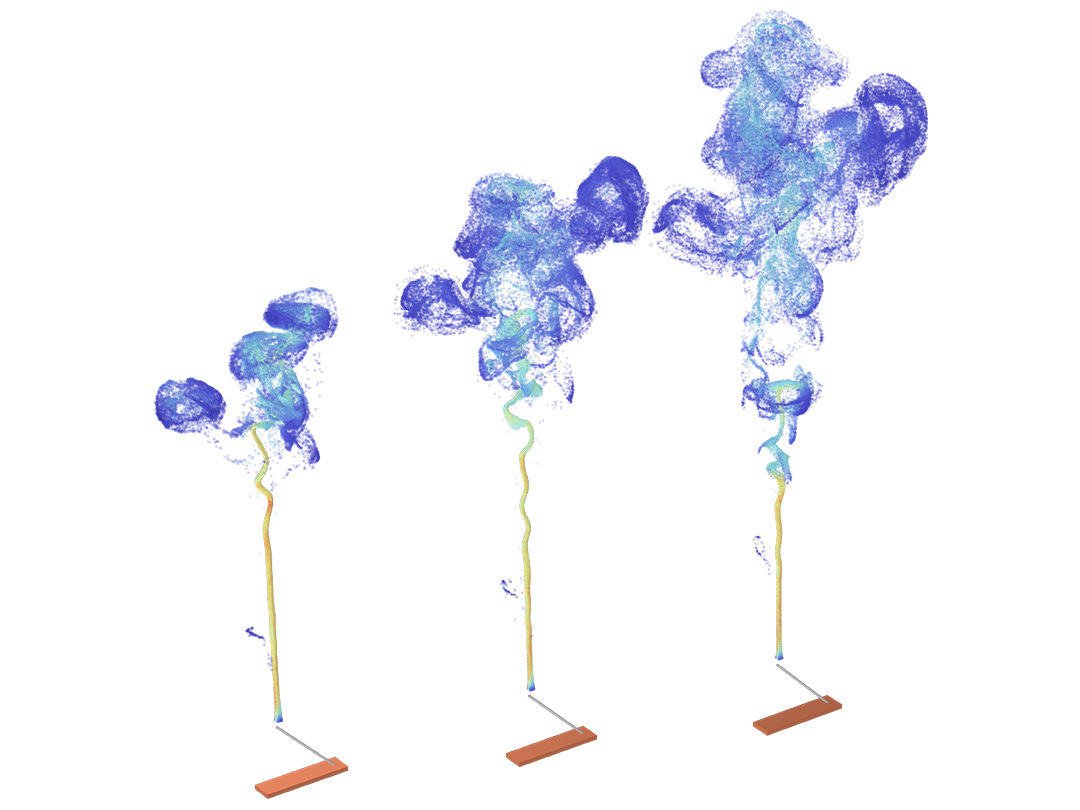Suivi de particules chargées
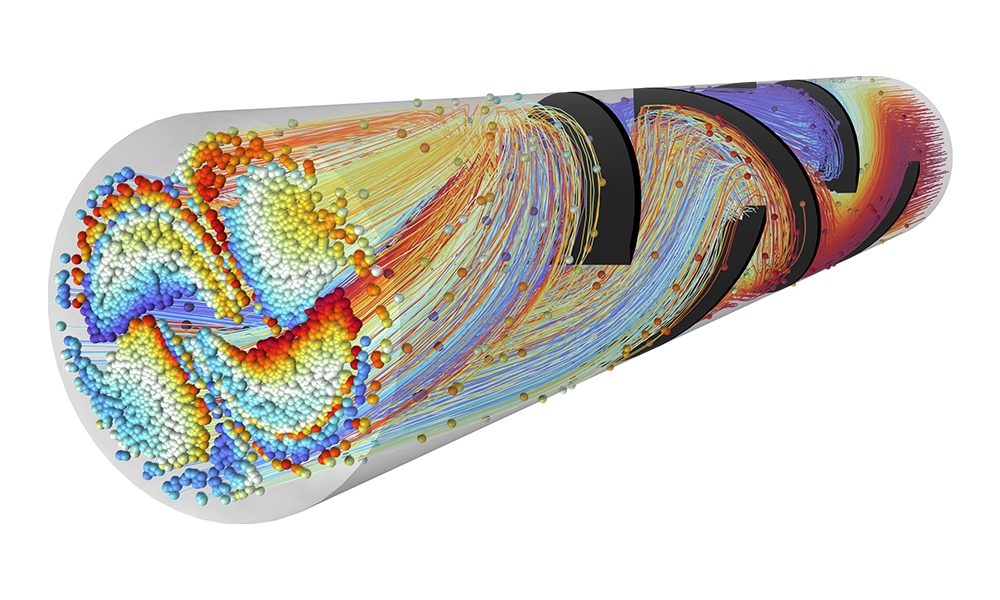
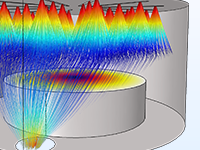
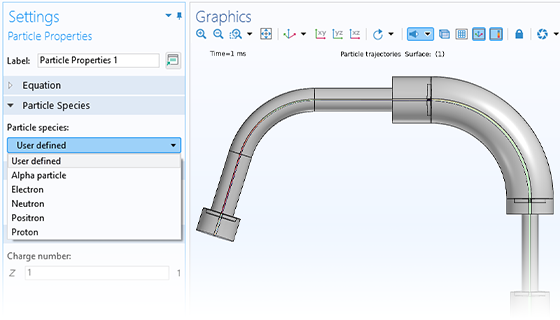
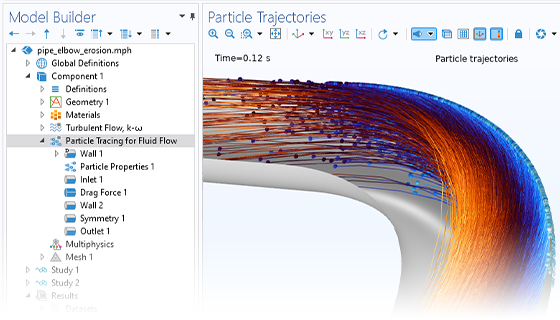
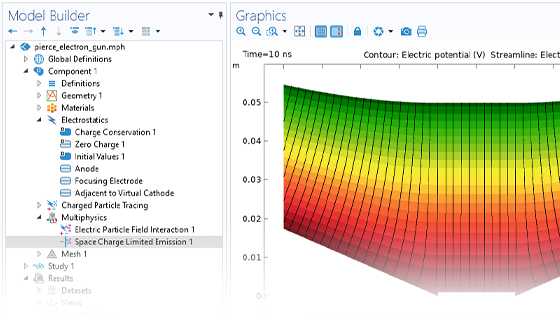
Calculer précisément les mouvements d'ions et d'électrons dans les champs appliqués est essentiel pour concevoir spectromètres, canons à électrons et accélérateurs de particules. Les champs électromagnétiques appliqués sont définis par l'utilisateur ou proviennent d'une analyse précédente. Ces champs peuvent être stationnaires, transitoires, ou dans le domaine fréquentiel. Il est possible d'appliquer autant de champs différents qu'il est nécessaire, ce qui permet de superposer des champs stationnaires et harmoniques dans la même simulation.
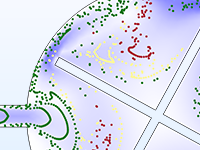
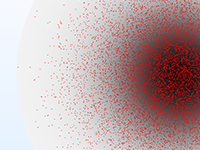
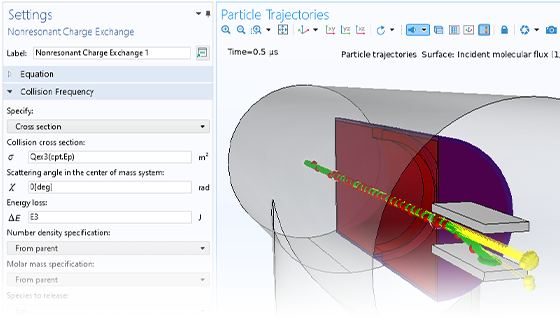
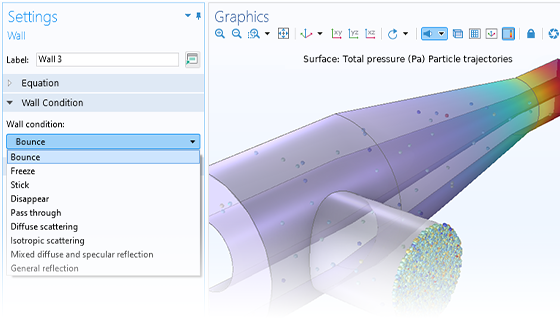
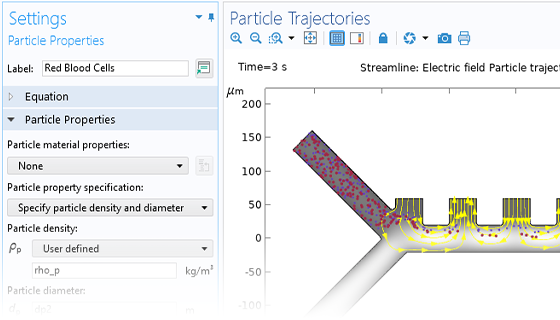
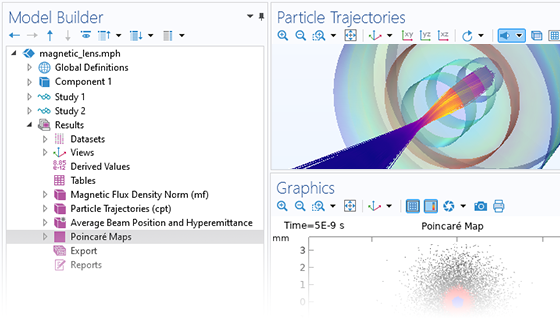
Le mouvement des particules a rarement lieu dans un vide parfait. N'importe quel modèle de suivi de particule peut être transformé en un modèle de collision de Monte Carlo, en donnant aux particules une probabilité d'entrer en collision avec des molécules du gaz environnant. Cela modifie la trajectoire des particules en changeant leur direction, ou engendre des réactions, par exemple une ionisation ou un échange de charges.
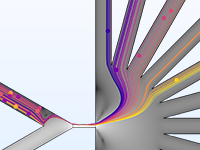
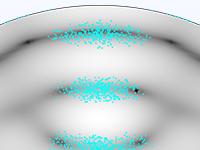
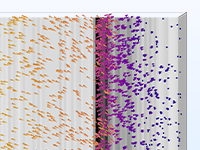
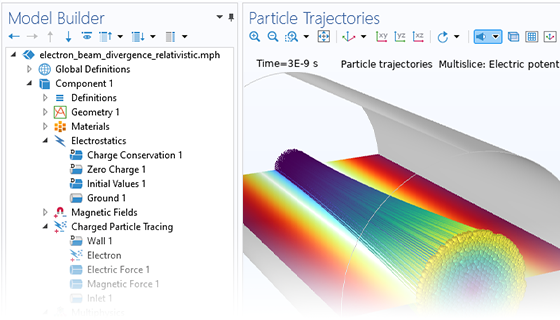
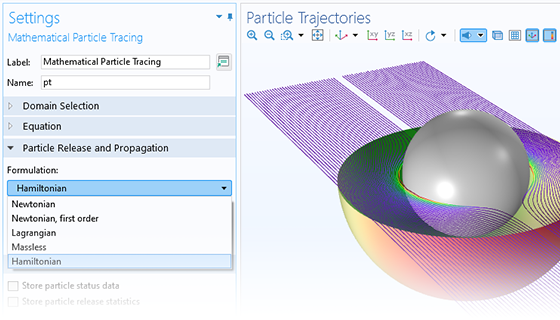
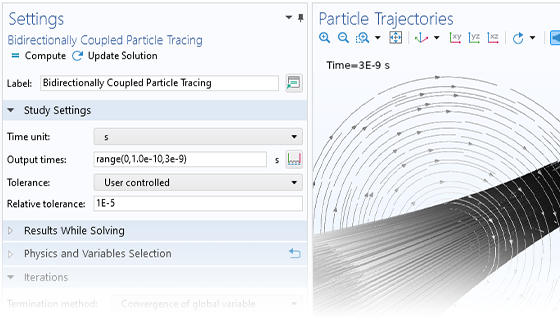
Le modèle le plus simple de suivi de particules chargées implique un couplage unidirectionnel, dans lequel les champs sont d'abord résolus puis utilisés pour définir les forces sur les particules. Si les particules chargées sont présentes dans le faisceau d'un courant suffisamment élevé, il peut être nécessaire de considérer le couplage bidirectionnel dans lequel les particules peuvent perturber les champs. Des analyses prédéfinies dédiées à ce type de couplage permettent d'implémenter facilement ces modèles couplés de façon bidirectionnelle.