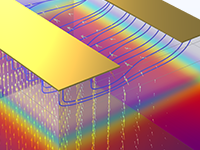
Transistors bipolaires 3D
Calculez la réponse courant-tension d'un transistor bipolaire et simulez le fonctionnement du dispositif en tant qu'amplificateur de courant analogique.
Module Semiconductor
Simuler des dispositifs semi-conducteurs et optoélectroniques
Le module Semiconductor offre des fonctionnalités dédiées à l'analyse du fonctionnement des dispositifs semi-conducteurs au niveau physique fondamentale. Un ensemble de types de dispositifs courants peut être simulé avec le module Semiconductor, comprenant les transistors bipolaires, les transistors à effet de champ métal-semi-conducteur (MESFET), les transistors à effet de champ métal-oxyde-semi-conducteur (MOSFET), les transistors bipolaires à grille isolée (IGBT), les diodes Schottky, les jonctions p-n, les cellules solaires, entre autres applications.
Le module comprend des fonctionnalités conçues pour modéliser les interactions entre les ondes électromagnétiques et les matériaux semi-conducteurs. Les dispositifs généralement modélisés sont les photodiodes, les diodes électroluminescentes et les diodes laser. De plus, le module permet d'utiliser des équations et des expressions définies par l'utilisateur dans le processus de modélisation.
Le module Semiconductor a également la flexibilité de pouvoir être combiné avec tout autre produit complémentaire de COMSOL Multiphysics®.
Contacter COMSOL
Ce que vous pouvez modéliser avec le module Semiconductor
Analysez différents types de transistors, de capteurs, de dispositifs photoniques, de systèmes quantiques et de composants de base des semi-conducteurs.
MOSFETs
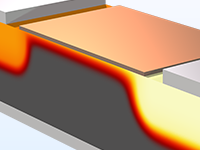
Calculez les caractéristiques en courant continu d'un transistor métal-oxyde-semi-conducteur (MOS).
Cellules solaires
Calculez la génération définie par l'utilisateur (déformée) et les taux de recombinaison de Shockley-Read-Hall des cellules solaires.
LEDs
Simulez une LED émettrice de lumière infrarouge.
Capteur ISFET
Couplez un modèle de semi-conducteur et un modèle d'électrolyte pour simuler un capteur de pH à transistor à effet de champ sensible aux ions (ISFET).
IGBT 3D
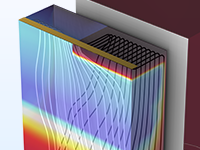
Modélisez un IGBT à grille à tranchée en disposant les émetteurs alternatifs le long de la direction d'extrusion, comme dans un dispositif réel.
FET à canal p
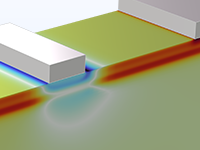
Analysez les caractéristiques en courant continu d'un FET à canal p en InSb, en utilisant la formulation du gradient de densité pour ajouter le confinement quantique.
Condensation de Bose-Einstein
Résolvez l'équation de Gross-Pitaevskii pour la formation d'un réseau de vortex dans un condensat de Bose-Einstein en rotation.
Caractéristiques et fonctionnalités du module Semiconductor
Les caractéristiques et les fonctionnalités du module Semiconductor sont décrites plus en détail ci-dessous.
Equations de dérive-diffusion
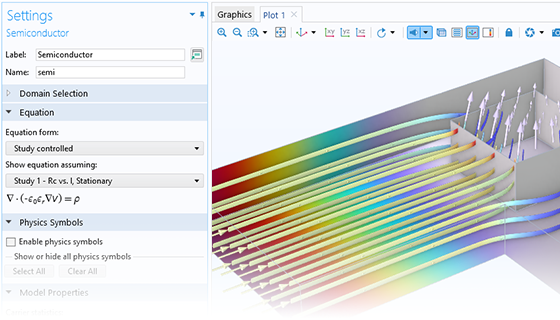
La pierre angulaire du module Semiconductor est l'interface Semi-conducteur, qui résout la combinaison des équations de dérive-diffusion et de Poisson. Cette interface permet de modéliser à la fois les domaines isolants et semi-conducteurs dans un dispositif semi-conducteur. Une application de la formulation de dérive-diffusion consiste à simuler la physique fondamentale d'un dispositif en utilisant les statistiques de Fermi-Dirac ou de Maxwell-Boltzmann.
Sont disponibles pour les équations de dérive-diffusion les types d'analyse en équilibre thermique, à l'état stationnaire, en réponse transitoire et en analyse en petits signaux.
Dopage et modèles de matériaux
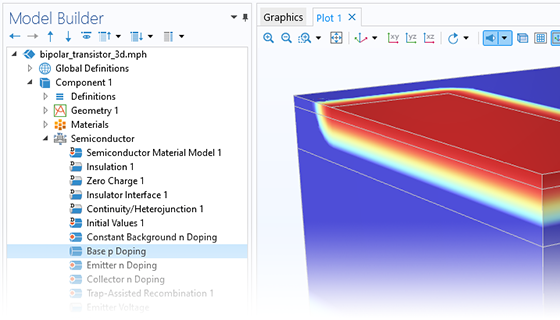
La spécification de la distribution du dopage d'un matériau est essentielle pour la modélisation des dispositifs semi-conducteurs. Le module Semiconductor comprend un ensemble de fonctionnalités qui permettent de réaliser pratiquement n'importe quel profil de dopage. Les options avancées comprennent l'ionisation incomplète et, pour les niveaux de dopage élevés, le rétrécissement de la bande interdite.
Les options de dopage intégrées contiennent les profils Linéaire, Gaussien, et Fonction d'erreur. Les profils de dopage définis par l'utilisateur sont spécifiés en saisissant une expression mathématique ou en utilisant les résultats d'une autre simulation comme base du profil de dopage.
En complément, il est facile de définir des profils de dopage basés sur des imports de fonctions tabulées. Cette stratégie est utile lorsque la distribution requise ne peut pas être définie analytiquement, comme par exemple si le profil de dopage est issu d'une simulation externe.
Contacts métal-semi-conducteur
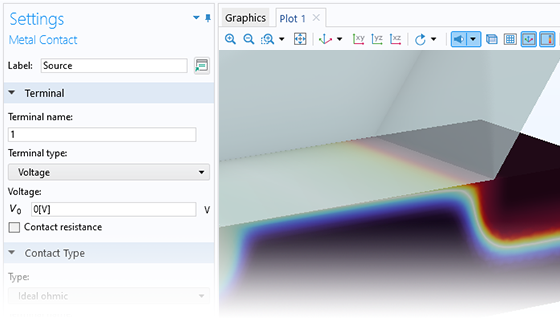
Une condition limite dédiée Contact métallique peut être utilisée pour modéliser des contacts métal-semi-conducteur. Ce type de terminal prend en charge une tension, un courant, une puissance et la connexion à un circuit externe.
Le type de contact de Schottky idéal est disponible pour modéliser une jonction métal-semi-conducteur à redressement simple où les caractéristiques courant-tension dépendent de la barrière de potentiel formée à la jonction. Pour incorporer les effets de recombinaison de surface et les densités de charge de surface provenant des pièges de surface dans ce modèle, des conditions limites Recombinaison de surface assistée par pièges peuvent être ajoutées à la même sélection de frontière que la condition de contact métallique.
Equation de Schrödinger
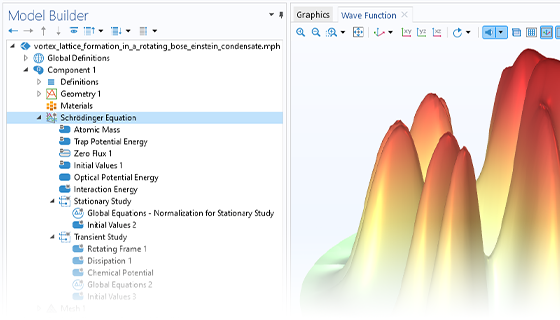
L'interface Equation de Schrödinger résout l'équation de Schrödinger pour une particule unique dans un potentiel externe. Cette interface est utile pour les problèmes généraux de mécanique quantique et les systèmes à confinement quantique, tels que les puits quantiques, les fils et les points (avec l'approximation de la fonction enveloppe).
Des conditions aux limites et des types d'étude appropriés sont mis en oeuvre pour que l'utilisateur puisse facilement configurer des modèles afin de calculer des quantités pertinentes dans diverses situations, telles que les énergies propres des états liés, les taux de désintégration des états quasi-liés, les coefficients de transmission et de réflexion, la condition d'effet tunnel résonnant et la bande interdite effective d'une structure en super-réseau.
Transitions optiques
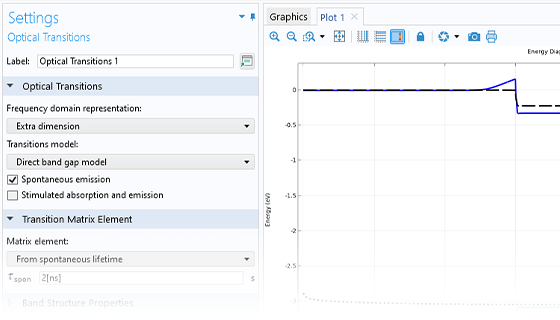
La fonctionnalité Transitions optiques permet de modéliser l'absorption optique et l'émission à la fois stimulée et spontanée au sein d'un semi-conducteur. L'émission ou l'absorption stimulée se produisent lorsqu'une transition a lieu entre deux états quantiques en présence d'un champ électrique oscillant, généralement produit par une onde électromagnétique qui se propage. L'émission spontanée se produit lorsque des transitions se produisent entre un état quantique de haute énergie et un état quantique de plus basse énergie.
Connexion aux circuits électriques
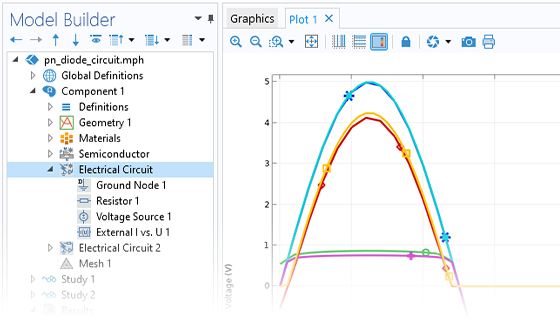
L'interface Circuit électrique est utilisée pour créer des systèmes réduits afin de modéliser les courants et les tensions dans les circuits. Cette fonctionnalité se révèle bénéfique lors de la modélisation de sources de tension et de courant typiques, de résistances, de condensateurs, d'inducteurs et d'autres dispositifs semi-conducteurs. Les modèles de circuits électriques peuvent également être connectés à des modèles de champs distribués en 2D et en 3D. En complément, les topologies de circuits peuvent être exportées et importées au format netlist SPICE. Les circuits électriques peuvent être combinés avec des modèles physiques de dispositifs semi-conducteurs pour simuler des charges réalistes, par exemple.
Modèles de mobilité des porteurs
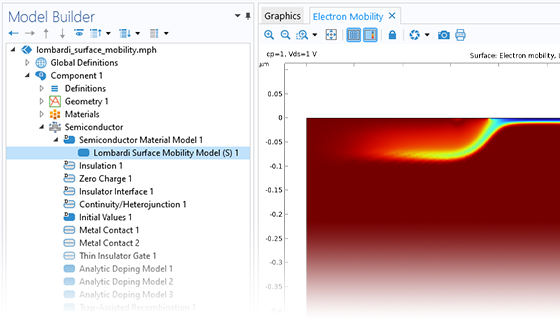
Des modèles réalistes pour la mobilité des porteurs sont importants lors de la simulation de dispositifs semi-conducteurs avec une approche de dérive-diffusion. Dans ce cas, la mobilité est limitée par la dispersion des porteurs dans le matériau. Le module Semiconductor comprend plusieurs modèles de mobilité prédéfinis ainsi que la possibilité pour les utilisateurs de définir leurs propres modèles de mobilité.
Les modèles de mobilité prédéfinis comprennent des options pour la diffusion des phonons, des impuretés et des porteurs, la saturation de la vitesse à haut champ et la diffusion de surface.
Les modèles de mobilité définis par l'utilisateur peuvent être facilement spécifiés en saisissant les expressions appropriées dans la fonctionnalité définie par l'utilisateur; il n'est pas nécessaire d'utiliser des scripts ou des codes. Ces modèles de mobilité définis par l'utilisateur peuvent être combinés arbitrairement avec les modèles de mobilité prédéfinis intégrés dans le logiciel.
Génération et recombinaison
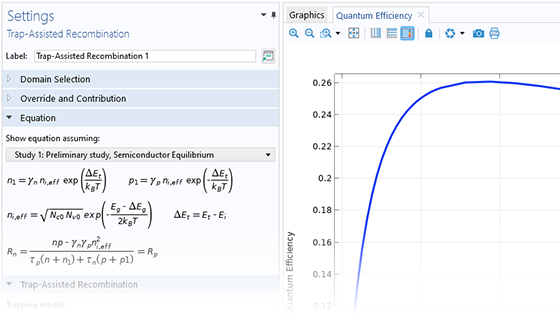
Les processus de génération et de recombinaison tels que la recombinaison d'Auger, la recombinaison directe, la génération par ionisation d'impact et la recombinaison assistée par pièges peuvent être inclus dans les modèles à l'aide de l'interface Semi-conducteur. Des caractéristiques de recombinaison et de génération définies par l'utilisateur sont disponibles pour définir manuellement les taux de ces processus.
Le modèle Recombinaison assistée par pièges est utilisé pour définir les taux de recombinaison des électrons et des trous dans les semi-conducteurs à bande interdite indirecte. Par défaut, la recombinaison en régime permanent est modélisée à l'aide du modèle de piégeage de Shockley-Read-Hall, qui prend en compte les états situés au niveau du milieu de la bande interdite. Un modèle de Distribution explicite des pièges peut également être utilisé pour spécifier des états discrets ou une densité continue d'états piégés à des énergies situées à l'intérieur de la bande interdite.
Contacts isolant-semiconducteur
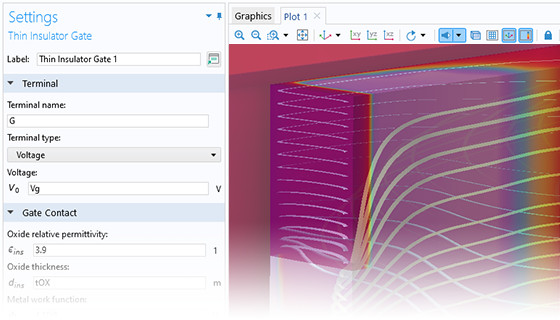
L'interface Semi-conducteur comprend une fonctionnalité permettant de modéliser un matériau isolant de faible épaisseur (oxyde) entre un semi-conducteur et un métal. Cette fonctionnalité supporte également l'analyse en petits signaux, utile pour le calcul des courbes I-V.
Pour modéliser un isolant général, une fonctionnalité de domaine de conservation de la charge peut être ajoutée à l'interface Semi-conducteur d'une manière similaire à la façon dont la fonctionnalité est ajoutée lors de la modélisation avec l'interface générale Electrostatique. Plusieurs conditions aux limites sont disponibles pour la modélisation d'un domaine isolant :
- Interface semi-conducteur-isolant
- Accumulation de charge sur la surface externe
- Champ de déplacement électrique
- Potentiel flottant
Equation de Schrödinger-Poisson
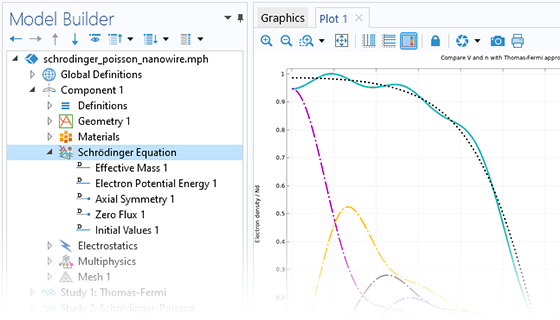
L'interface multiphysique Equation de Schrödinger-Poisson combine l'interface Equation de Schrödinger et l'interface Electrostatique pour modéliser les porteurs de charge dans les systèmes à confinement quantique. Cette interface peut être utilisée pour modéliser des dispositifs à confinement quantique tels que des puits quantiques, des fils et des points, ainsi que des fonctions d'onde multicomposantes pour modéliser des systèmes multibandes et des particules dotées d'un spin. De plus, elle permet de simuler des systèmes quantiques généraux, tels que la formation d'un réseau de vortex dans un condensat de Bose-Einstein.
Lors de l'utilisation de l'interface Equation de Schrödinger-Poisson, le potentiel électrique contribue au terme d'énergie potentielle dans l'équation de Schrödinger, et une somme statistiquement pondérée des densités de probabilité des états propres contribue à la densité de charge d'espace. Un type d'étude spécifique est disponible pour générer automatiquement les paramètres du solveur requis par la solution auto-cohérente du système en couplage bidirectionnel.
L'interface comprend une option permettant de modéliser une frontière ouverte avec des ondes entrantes et sortantes, qui est utilisée pour simuler des conditions de tunnel résonnant. En complément, une condition limite Condition périodique est disponible pour modéliser les super-réseaux.
Optoélectronique dans les semi-conducteurs
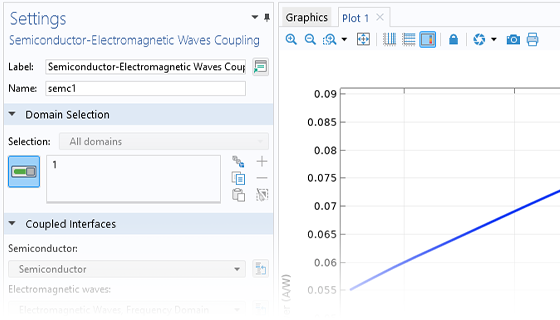
Le module Semiconductor comprend deux interfaces multiphysiques pour modéliser l'interaction entre les ondes électromagnétiques et les semi-conducteurs. Pour utiliser cette fonctionnalité, le Module Wave Optics est nécessaire. La fonctionnalité est basée sur les interfaces Domaine fréquentiel et Enveloppes de faisceau du module Wave Optics.
Les couplages entre les interfaces Semi-conducteur et Ondes électromagnétiques sont réalisés grâce à la fonctionnalité Transitions optiques du module Semiconductor. Cette fonctionnalité introduit un terme de génération d'émission stimulée sur les domaines à l'intérieur de l'interface Semi-conducteur, qui est approprié pour les matériaux à bande interdite directe. Ce terme est proportionnel à l'intensité optique dans la fonctionnalité correspondante de l'interface Ondes électromagnétiques. De plus, la fonctionnalité Transitions optiques peut également prendre en compte l'émission spontanée dans les matériaux à bande interdite directe.
L'effet de l'absorption ou de l'émission de lumière est pris en compte par un changement correspondant de la permittivité complexe ou de l'indice de réfraction.
Multiphysique des dispositifs semi-conducteurs
Les effets physiques couplés jouent souvent un rôle important dans les performances des dispositifs semi-conducteurs. En combinant différentes physiques, telles que l'électrostatique, le transfert de chaleur, l'optique ondulatoire, l'optique géométrique et le transport des espèces chimiques, les simulations multiphysiques peuvent saisir les interactions complexes qui se produisent dans les dispositifs semi-conducteurs. Voici quelques exemples d'analyses multiphysiques de dispositifs semi-conducteurs :
- Modélisation des effets thermiques à l'intérieur d'un dispositif de puissance
- Illumination de cellules solaires en silicium par modélisation des rayons solaires
- Modélisation de l'émission stimulée et spontanée en tenant compte de l'optique ondulatoire
- Couplage d'un modèle de semi-conducteur et d'électrolyte utilisant le transport d'espèces
La combinaison du module Semiconductor avec d'autres produits de la suite logicielle COMSOL permet une analyse multiphysique qui fournit une compréhension plus réaliste et plus complète du comportement des dispositifs semi-conducteurs. Cela mène au développement de dispositifs semi-conducteurs plus efficaces et plus avancés, avec des performances et des capacités améliorées.
Chaque activité et chaque besoin en matière de simulation sont différents.
Afin d'évaluer pleinement si le logiciel COMSOL Multiphysics® répond ou non à vos exigences, nous vous invitons à nous contacter. En parlant à l'un de nos représentants, vous obtiendrez des recommandations personnalisées et des exemples détaillés qui vous aideront à tirer le meilleur parti de votre évaluation et vous guideront pour choisir les options de licence les plus adaptées à vos besoins.
Il vous suffit de cliquer sur le bouton "Contacter COMSOL", d'indiquer vos coordonnées et tout commentaire ou question spécifique, avant de soumettre votre demande. Vous recevrez une réponse d'un représentant de COMSOL très rapidement.
Prochaine étape:
Demander une démonstration du logiciel